Gravitation
Based on Class 10 -Science & Technology-Chapter 1- Maharashtra Board
Notes
| Topics to be learn :
Gravitation, Circular motion and centripetal force, Kepler’s laws, Newton’s universal law of gravitation, Acceleration due to the gravitational force of the Earth, Free fall, Escape velocity.
|
Gravitational force: There exists a force of attraction between any two particles of matter in the universe such that the force depends only on the masses of the particles and the separation between them. It is called the gravitational force and the mutual attraction is called gravitation.
The gravitational force between the earth and the moon. The gravitational force is a universal force, i.e., it acts between any two objects in the universe.
Electromagnetic force: The force between two charged particles in motion.
Nuclear force: The force between a proton and a neutron in the nucleus of an atom.
Centripetal force : In uniform circular motion of a body, the force acting on the body is directed towards the centre of the circle. This force is called centripetal force.
Thus, a force acts on any object moving along a circle and it is directed towards the centre of the circle. This is called the centripetal force. ‘Centripetal’ means centre seeking, i.e., the object tries to go towards the centre of the circle because of this force.
Example : The moon revolves around the earth due to the gravitational force exerted on it by the earth. This force is directed towards the centre of the earth and is thus a centripetal force.
Effects of a force acting on an object : ( Note: a body = an object) (i) A force can set a body in motion. For example, if a ball at rest on the floor is pushed, it rolls on the floor. (ii) A force can stop a moving body. For example, a moving bicycle can be brought to rest by application of brakes. (iii) A force acting on a body can change the speed of the body. For example, when brakes are applied to a moving bicycle, its speed decreases due to the friction between the brake shoes and the rim of the tyre. (iv) A force can change the direction of motion of the body. For example, in uniform circular motion of a body, the direction of motion of the body keeps on changing due to the applied force. (v) A force can change the speed as well as the direction of motion of the body. For example. when a. ball bowled by 4 bowler is hit by a batsman, there occurs a Change in the speed as well as direction of motion of the ball. (vi) A force can change the shape and size of the body on which it acts. For example, when a rubber ball is pressed, it gets deformed and hence no longer remains spherical. Also that can be a decrease in volume.
(1) Newton’s first law of motion: An object continues to remain at rest or in a state of uniform motion along a straight line unless an external unbalanced force acts on it.
(2) Newton’s second law of motion : The rate of change of momentum is proportional to the applied force and the change of momentum occurs in the direction of the force.
(3) Newton’s third law of motion: Every action force has an equal and opposite reaction force which acts simultaneously. [ Equal in magnitude and opposite in direction. ]
Kepler's laws of planetary motion –
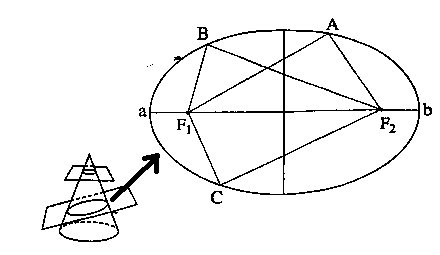
First Law: The orbit of a planet is an ellipse with the Sun at one of the foci.
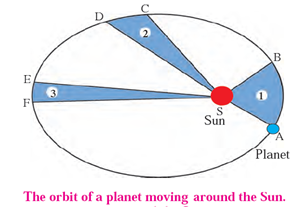
Figure shows the elliptical orbit of a planet revolving around the Sun. S denotes the position of the Sun.
Second Law: The line joining the planet and the Sun sweeps equal areas in equal intervals of time.
AB, CD and EF are distances covered by the planet in equal intervals of time.
The straight lines AS, CS and ES sweep equal areas in equal intervals of time.
Area ASB = Area CSD = Area ESF.
Third Law: The square of the period of revolution of a planet around the Sun is directly proportional to the cube of the mean distance of the planet from the Sun.
\(\text{(period of revolution)}^2 ∝(\frac{ab}{2})^3\)
Thus, if r is the average distance of the planet from the Sun and T is its period of revolution, then,
T2 ∝ r3,
i.e., T2/ r3 = constant = K.
Newton's universal law of gravitation : Every object in the Universe attracts every other object with a definite force. This force is directly proportional to the product of the masses of the two objects and inversely proportional to the square of the distance between them.
As the law of gravitation given by Newton is applicable throughout the universe and to all particles. Hence it is called universal law.
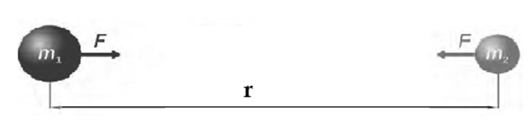
Mathematical form of Newton's universal law of gravitation: Consider two objects of masses m1 and m2. We assume that the objects are very small spheres of uniform density and the distance r between their centres is very large compared to the radii of the spheres (Fig.). The magnitude (F) of the gravitational force of attraction between the objects is directly proportional to m1m2 and inversely proportional to r2 ∴ \(F ∝ \frac{(m_1 m_2)}{r^2}\) , ∴ \(F=\frac{(Gm_1 m_2)}{r^2}\) Where G is the constant of proportionality, called the universal gravitational constant. The above law means that if the mass of one object is doubled, the force between the two objects also doubles. Also, if the distance is doubled, the force decreases by \(\frac{1}{4}\) .
The importance of Newton’s universal law of gravitation : This law explains successfully, i.e., with great accuracy,
Q. Why is the constant of gravitation called a universal constant?
Hence, it is called a universal constant.
The earth’s gravitational force: The gravitational force on any object due to the earth is always directed towards the centre of the earth. If the object is on the earth’s surface, in the usual notation.
\(F=\frac{(Gm_1 m_2)}{r^2}\)
- As the earth’s centre of mass is at its centre, the gravitational force exerted by the earth on any object is always directed towards the earth’s centre.
- Hence, an object released from a point above the earth’s surface falls vertically downward towards the earth.
- If an object is thrown vertically upward, its velocity goes on decreasing due to the earth’s gravitational force on the object. At one stage, the velocity of the body becomes zero and later the body falls back to the earth.
The earth's gravitational acceleration : The acceleration produced in a body due to the earth’s gravitational force is called the acceleration due to gravity or the earth’s gravitational acceleration and its magnitude is denoted by g. It is directed towards the earth’s centre. Suppose that a body of mass m is released from a distance r from the centre (O) of the earth. Let M be the mass of the earth. According to newton’s law of the gravitation the magnitude of the earth’s gravitational force acting on the body is \(F = G\frac{Mm}{r^2}\) Where G is the universal constant of gravitation The acceleration produced by this force, g =Force/mass = F/m ∴ \(g = \frac{GM}{r^2}\) This is the formula for the acceleration due to gravity or the gravitational acceleration due to the earth. This acceleration is directed towards the earth's centre. If h denotes the altitude, r = R + h, where R is the radius of the earth. \(g = \frac{GM}{(R+h)^2}\) For a body on the earth's surface, h = 0 \(g = \frac{GM}{R^2}\) \(g=\frac{GM}{r^2}\) for r ≥ R (radius of the earth). It depends on the location of the body.
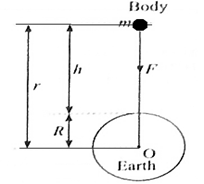
Factors affecting the value of g : The value of the acceleration due to gravity, g, changes from place to place on the earth. It also varies with the altitude and depth below the earth’s surface. The factors affecting the value of g are the shape of the earth, altitude and depth below the earth’s surface. (1) The earth is not perfectly spherical. It is somewhat flat at the poles and bulging at the equator. At the surface of the earth, the value of g is maximum (9.832 m/s2) at the poles as the polar radius is minimum, It is minimum (9.78 m/s2) at the equator as the equatorial radius is maximum. (2) As the height (h) above the earth’s surface increases, the value of g decreases It varies as 1/(R+h)2 where R is radius of the earth. (3) In the interior of the earth, on the average the value of g is less than that at the earth’s surface. As the depth below the earth’s surface increases the value of g decreases and finally it becomes zero at the centre of the earth.
Mass & Weight :
| Mass | Weight |
|
|
Free fall : Whenever an object moves under the influence of gravity alone, it is said to be falling freely.
For a freely falling object, with u =0 and α =g,
we have \(v=gt, s=\frac{1}{2}gt^2\text{ and } v^2=2gs\) (in the usual notation).
For an object thrown upward, as the object moves upward, the direction of acceleration is opposite to that of the velocity. Hence, the acceleration is negative, with α = —g.
When a body falls in air, there are three forces acting on the body:
- the gravitational force due to the earth, acting downward
- the force of buoyancy (upthrust) due to air, acting upward
- the force due to friction with air (called air resistance) acting upward (being always in the direction opposite to that of the velocity of the body)
Under certain conditions, the force of buoyancy due to air and friction with air can be ignored compared to the gravitational force of the earth. In that case (near the earth's surface) the body fallswith almost uniform acceleration (g).
Whenever a body moves under the influence of the force of gravity alone, it is said to be falling freely. Strictly speaking, this is true only if the body falls in vacuum.
The corresponding kinematical equations of motion, in the usual notation, are
v = u+gt, s = ut + ½ gt2 and v2 = u2 + 2gs
During a free fall, heavier object and a fighter one both objects will have the same acceleration.
Gravitational potential energy : The energy stored in a body due to the gravitational force between the body and the earth is called the gravitational potential energy.
The gravitational potential energy of an object at a height h from the earth’s surface
= \(-\frac{GMm}{R+H}= -\frac{mgR^2}{R+h}\)
Escape velocity : When a body is thrown vertically upward from the surface of the earth, the minimum initial velocity of the body for which the body is able to overcome the downword pull by the earth and can escape the earth is called the escape velocity.
Expression for the escape velocity, using the law of conservation of energy: Here effects of air is not considered. Suppose a body of mass m is thrown vertically upward from the surface of the earth. Let the initial velocity of the body be the escape velocity (vesc). When the body is on the earth’s surface, its total energy E1 = kinetic energy + potential energy = ½ mv2esc + (-GmM/R) where G = universal gravitational constant, M =mass of the earth and R = radius of the earth. Thus, E1 = ½ mv2esc -GmM/R When the body moves to infinity and comes to rest there, its total energy, E2 =½ m(0)2 -GmM/¥ = 0+0=0. According to the law of conservation of energy, E1 = E2. ½ mv2esc -GmM/R = 0 ∴ ½ v2esc = GM/R ∴ v2esc = 2GM/R \(v_{esc}=\sqrt{\frac{2GM}{R}}\) This is the required expression. Escape velocity in terms of g and R We know g= GM/R2 \ GM = gr2 \(v_{esc}=\sqrt{\frac{2GM}{R}}= \sqrt{2gR}\)
Difference between Universal gravitational constant and gravitational acceleration of the earth: numerically equals the force of attraction between two unit masses separated by a unit distance. earth is the acceleration produced in a body due to the gravitational force of the earth.
Universal gravitational constant
Gravitational acceleration of the earth
1-The universal gravitational constant
The gravitational acceleration of the
2-Its value remains constant throughout the universe.
Its value changes from place to place.
3-It has magnitude but not direction.
It has both magnitude and direction.
4- Its SI unit is N-m2/kg.
Its SI unit is m/s2.
Important Formulae : The total energy of a body revolving around the earth =kinetic energy + potential energy \(=\frac{1}{2}(mv^2 )+\left(-\frac{GMm}{R+h})\right)\) Uniform circular motion of a planet around the Sun: (1) Centripetal force acting on the planet, \(\frac{mv^2}{r}\) gravitational force exerted by the Sun on the planet, (2) Centripetal acceleration of the planet, \(a=\frac{v^2}{r}=\frac{(\frac{2πr}{T})^2}{r}=\frac{4π^2r}{T^2}\) (3) The period of revolution of the planet, \(T=\frac{2πr}{v}=\frac{2π}{\sqrt{GM}}r^{\frac{3}{2}}=\frac{2π}{\sqrt{gR^2}}r^\frac{3}{2}\)

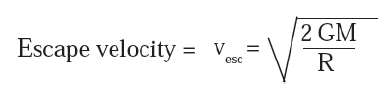
Useful links :
| Main Page : - Maharashtra Board Class 10 Science & Technology Part-1,Part-2 - All chapters notes, solutions, videos, test, pdf.
Books : MSBSHSE -Class 10th Science Text Books – Chapter wise PDF for download Next Chapter : Class 10-Sc. & Tech.-1-Chapter-2-Periodic Classification of Element - Online Notes |
It’s so useful
Thanks for this notes and it’s so usefull for me
YOUR NOTES IS VERY NICE AND SIMPLE
BUT 1 PROBLEM CAN YOU REMOVE THIS ARROW ON SCROLLING
Its useful for desktop and some long pages.Thanks for contact us
Nice teaching
It is very helpful for me
Very good
Thank you for this notes 🙏🏻 This is useful for me 🙏🏻☺️
Thank you for your notes 🙏🙏 my study is very important ❤️ to your notes
Thanks for nots pdf is a very nice and so useful
Thank you.. it was a lot helpful for preparing my science notes :))
Thanks for this notes 📝It is very useful for me and my friends again thank you for your notes
Very helpful for me
Thank you.. it helped me a lot for preparing my science notes :))
Hey amruta did you had written these all notes in your book
thnks it is very helpfull
nice
very usefull notes.
in 10th science 1
chaper nó 1
gravitation
It’s too Good…
Thanks
It helped me a lot…🙏🏻🙂🙂
Thank you very much!! this helped me a lot in my exams.
Thank you very much!! this helped me a lot in my exams.
Thank you so much it’s very helpful.
It’s very useful for me . This is too good. I Like very very much 😊 thanks for this notes .
it is so useful and important
It is so useful and important
Thank you mam for notes🥰 ______ it’s very helpful for me in rivision
Thanks …..it helps me for the better understanding
Thanks for this notes and it’s so usefull for me
thanks…….. it helps me for study ..
Thanks for this notes it’s so usefull
Nice notes and very useful for preparing study thank you for making this note👍
GOOD BUT THIS IS TO COPY
Thank you 💜🤗
I was start today for learning notes & thank you for notes 💜💝
BEST
It’s very useful and very 👍🙂
Thanks for notes
NICE NOTES
NICE TEACHING TOO
Thank you sir