Gravitation
Based on Class 10 -Science & Technology-Chapter 1- Maharashtra Board
Solution
Question 1:
Study the entries in the following table and rewrite them putting the connected items in a single row.
| I | II | III |
| Mass | m/s2 | Zero at the centre |
| Weight | kg | Measure of inertia |
| Acceleration due to gravity | Nm2/kg2 | Same in the entire universe |
| Gravitational constant | N | Depends on height |
Answer:
I
II
III
Mass
kg
Measure of inertia
Weight
N
Depends on height
Acceleration due to gravity
m/s2
Zero at the centre
Gravitational constant
Nm2/kg2
Same in the entire
universe
Question 2:
Answer the following questions. Difference between mass and weight of an object is as follows: The mass of an object on the Earth will be same as that on Mars but its weight on both the planets will be different. This is because the weight (W) of an object at a place depends on the acceleration due to gravity of that place i.e. \(W=mg\) or \(W∝mg\) and since the values of acceleration due to gravity on both the planets differ, thus the weight of the object will be different for both the planets.
(a) What is the difference between mass and weight of an object. Will the mass and weight of an object on the earth be same as their values on Mars? Why?
S. No.
Mass
Weight
1.
Mass is the amount of matter contained in a body.
Weight is the force exerted on a body due to the gravitational pull of another body such as Earth, the sun and the moon.
2.
Mass is an intrinsic property of a body.
Weight is an extrinsic property of a body.
3.
Mass is the measure of inertia.
Weight is the measure of force.
4.
The mass of a body remains the same everywhere in the universe.
The weight of a body depends on the local acceleration due to gravity where it is placed.
5.
The mass of a body cannot be zero.
The weight of a body can be zero.
6.
The SI unit of mass is kilogram (kg).
Since weight is a force, its SI unit is newton (N).
7.
The mass of a body can be measured using a beam balance and a pan balance.
The weight of a body can be measured using a spring balance and a weighing machine.
(b) What are (i) free fall, (ii) acceleration due to gravity (iii) escape velocity (iv) centripetal force ?
(i) Free fall : A body is said to be under free fall when no other force except the force of gravity is acting on it. \(v_{esc}=\sqrt{\frac{2GM}{R}}= \sqrt{2gR}\) (iv) The force required to keep an object under circular motion is known as centripetal force. This force always acts towards the centre of the circular path.
(ii) Acceleration due to gravity : The acceleration with which an object moves towards the centre of Earth during its free fall is called acceleration due to gravity. It is denoted by the letter ‘g’. It is a constant for every object falling on Earth’s surface.
(iii) Escape velocity : The minimum velocity required to project an object to escape from the Earth's gravitational pull is known as escape velocity. It is given as:
(c) Write the three laws given by Kepler. How did they help Newton to arrive at the inverse square law of gravity?
Three laws given by Kepler is as follows: Third Law: The squares of the periodic times of the planets are proportional to the cubes of their mean distances from the Sun. Newton used Kepler’s third law of planetary motion to arrive at the inverse-square rule. He assumed that the orbits of the planets around the Sun are circular, and not elliptical, and so derived the inverse-square rule for gravitational force using the formula for centripetal force. This is given as: where, m is the mass of the particle, r is the radius of the circular path of the particle and v is the velocity of the particle. Newton used this formula to determine the force acting on a planet revolving around the Sun. Since the mass m of a planet is constant, equation (i) can be written as \(F ∝ \frac{v^2}{r}\) ...(ii) where, r is the radius of the circular orbit of the planet or, On squaring both sides of this equation, we get: \(v^2∝\frac{r^3}{T^2}×\frac{1}{r}\) ...(vi) Hence, equation (vi) becomes: \(v^2∝\frac{1}{r}\) ...(vii) \(F∝\frac{1}{r^2}\) Hence, the gravitational force between the sun and a planet is inversely proportional to the square of the distance between them.
First Law: The orbits of the planets are in the shape of ellipse, having the Sun at one focus.
Second Law: The area swept over per hour by the radius joining the Sun and the planet is the same in all parts of the planet’s orbit.
\(F =\frac{mv^2}{r}\) ...(i)
Now, if the planet takes time T to complete one revolution around the Sun, then its velocity v is given as:
\(v=\frac{2πr}{T}\) ...(iii)
\(v∝\frac{r}{T}\) ...(iv) [as the factor 2π is a constant]
\(v^2∝\frac{r^2}{T^2}\) ...(v)
On multiplying and dividing the right-hand side of this relation by r, we get:
According to Kepler’s third law of planetary motion, the factor \(\frac{r^3}{T^2}\) is a constant
On using equation (vii) in equation (ii), we get:
(d) A stone thrown vertically upwards with initial velocity u reaches a height ‘h’ before coming down. Show that the time taken to go up is same as the time taken to come down.
For vertical upward motion of the stone: →\(-2gh=0-u^2\) \(u=\sqrt{2gh}\) Now, from first equation of motion, we have \(v=u-gt\) \(t=\frac{u}{g}\) \(t=\sqrt{\frac{2h}{g}}\) ......(i) For vertical downward motion of the stone: Let t' be the time taken by the ball to reach the ground. Thus, using second equation of motion, we have \(2gh=(v')^2\) \(v'=\sqrt{2gh}\) Now, from first equation of motion, we have \(v'=u+gt'\) \(t'=\frac{v'}{g}\) \(t'=\sqrt{\frac{2h}{g}}\) .....(ii) Hence, from (i) and (ii), we observe that the time taken by the stone to go up is same as the time taken by it to come down.
S = h
u = u
v = 0
a = -g
Let t be the time taken by the ball to reach height h. Thus, using second equation of motion, we have
\(-2gh=v^2-u^2\)
S = h
u = 0
a = g
Let v' be the velocity of the ball with which it hits the ground.
(f) If the value of g suddenly becomes twice its value, it will become two times more difficult to pull a heavy object along the floor. Why?
Let the mass of the heavy object be m. Thus, the weight of the object or the pull of the floor on the object is Now, if g becomes twice, the weight of the object or the pull of the floor on the object also becomes twice i.e. W'=2mg=2W Thus, because of doubling of the pull on the object due to the floor, it ill become two times more difficult to pull it along the floor.
W=mg
Question 3:
Explain why the value of g is zero at the centre of the earth.
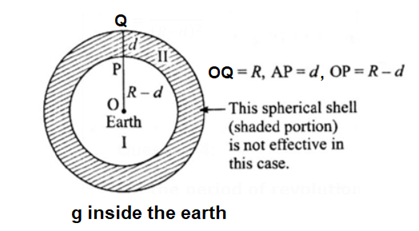
The value of g changes while going deep inside the earth. It goes on decreasing as We go from the earth’s surface towards the earth’s centre. We shall treat the earth as a sphere of uniform density. If We consider a particle of mass m at point P at a distance (R - d) from the earth’s centre, where R is the radius of the earth and d is the depth below the earth’s surface, the gravitational force on the particle due to the earth is F = \(\frac{GmM'}{(R-d)^2}\) where M’ is the mass of the sphere of radius (R-d) M' = \(\frac{4}{3}π(R-d)^3×\frac{M}{\frac{4}{3}πR^3}\) = \(\frac{M(R-d)^3}{R^3}\) This is because the outer spherical shell is not effective (Fig.). In this case, the acceleration due to gravity is g = \(\frac{F}{m}=\frac{G}{(R-d)^2}×\frac{M(R-d)^3}{R^3}=\frac{GM(R-d)}{R^3}\) where M is the mass of the earth. Thus, g decreases as d increases. It is less than that at the earth’s surface \((\frac{GM}{R^2})\). At the earth’s centre, d = R ∴ g= 0
Question 4:
Let the period of revolution of a planet at a distance R from a star be T. Prove that if it was at a distance of 2R from the star, its period of revolution will be \(\sqrt{8}T\).
From Kepler's third law of planetary motion, we have \(T^2∝r^3\) ......(i) Thus, when the period of revolution of planet at a distance R from a star is T, then from (i), we have \(T^2∝R^3\) ......(ii) Now, when the distance of the planet from the star is 2R, then its period of revolution becomes \((T_1)^2∝(2R)^3\) \((T_1)^2∝8R^3\) ......(iii) Dividing (iii) by (ii), we get \(\frac{(T_1)^2}{T^2} =\frac{8R^3}{R^3}\) Therefore \(T_1=\sqrt{8}T\)
Question 5:
Solve the following examples.
(a) An object takes 5 s to reach the ground from a height of 5 m on a planet. What is the value of g on the planet?
Here, u = 0 Hence, the value of g on the planet is 0.4 m/s2.
S = 5 m
t = 5 s
From second equation of motion, we have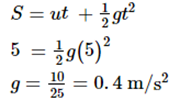
(b) The radius of planet A is half the radius of planet B. If the mass of A is MA, what must be the mass of B so that the value of g on B is half that of its value on A?
The acceleration due to gravity of a planet is given as \(g=\frac{GM}{r^2}\) For planet A \(g_A=\frac{GM_A}{(r_A)^2}\) For planet B \(g_B=\frac{GM_B}{(r_B)^2}\) Now \(g_B=\frac{1}{2}g_A\) (Given) or \(\frac{GM_B}{(r_B)^2}=\frac{GM_A}{2(r_A)^2}\) \(M_B=\frac{M_A(r_B)^2}{2(r_A)^2}\) Given \(r_A=\frac{1}{2}r_B\) ∴ \(M_B=\frac{M_A(r_B)^2}{2\frac{1}{2}(r_B)^2}=2M_A\) Thus, the mass of planet B should be twice that of planet A.
(c) The mass and weight of an object on earth are 5 kg and 49 N respectively. What will be their values on the moon? Assume that the acceleration due to gravity on the moon is 1/6th of that on the earth.
Mass of the object on Earth, m = 5 kg \(W_M=\frac{1}{6}W_E\) \(W_M=\frac{49}{6}\) \(W_M=8.17N\) Weight of the object on Moon =8.17N Mass of the object on Moon = 5 kg (since mass is independent of the place of observation)
Weight of the object on Earth, WE = 49 N
Weight of the object on Moon
(d) An object thrown vertically upwards reaches a height of 500 m. What was its initial velocity? How long will the object take to come back to the earth? Assume g = 10 m/s2
For vertical upward motion of the object, \(0-u^2=-2×10×500\) \(u=100m/s\) Now, let t1 be time taken by the object to reach at 500 m height. Thus \(v=u+at\) \(0=100-10t_1\) \(t_1=10s\) For vertical downward motion of the object, \(S=ut+\frac{1}{2}gt^2\) \(500=\frac{10}{2}× (t_2)^2\) \(t_2=10s\) Thus, the total time taken by the object to reach back to Earth = t1 + t2 = 20s
S = 500 m
g = - 10 m/s2
v = 0
Let u be the initial velocity of the object. From third equation of motion, we have
\(v^2-u^2=2gS\)
S = 500 m
g = 10 m/s2
u = 0
Let t2 be the time taken by the object to come back to the Earth from height of 500 m. From second equation of motion, we have
(e) A ball falls off a table and reaches the ground in 1 s. Assuming g = 10 m/s2, calculate its speed on reaching the ground and the height of the table.
Here, t =1 s \(S=ut+\frac{1}{2}gt^2\) \(h=0+\frac{1}{2}×10×1^2\) \(h=5m\) Hence, the height of the table is 5 m.
g = 10 m/s2
u = 0
Let v be the velocity of the ball on reaching the ground.
Thus, from first equation of motion, we have
v = u + gt
⇒v = 10×1 = 10 m/s
Hence, the speed of the object on reaching the ground is 10 m/s.
Let h be the height of the table. Thus, from second equation of motion, we have
(f) The masses of the earth and moon are 6 × 1024kg and 7.4 × 1022kg, respectively. The distance between them is 3.8 × 105 km. Calculate the gravitational force of attraction between the two? Use G = 6.7 × 10–11 N m2 kg–2
The gravitational force between the Moon and the Earth can be found out using the formula, \(F=\frac{GM_eM_m}{r^2}\) where, Me and Mm are the masses of the Earth and the Moon, respectively. Using all the given values, we have \(F= \frac{(6.7×10^{-11})(6×10^{24})(7.4×10^{22})}{(3.8×10^5×1000)^2}\) = 20.6×1019 ≅ 2×1020N F = 2 × 1020 N
(g) The mass of the earth is 6 × 1024kg. The distance between the earth and the sun is 1.5 × 1011m. If the gravitational force between the two is 3.5 × 1022 N, what is the mass of the sun? Use G = 6.7 × 10-11 Nm2 kg–2
The gravitational force between the Sun and the Earth can be found out using the formula, \(F=\frac{GM_eM_s}{r^2}\) where, Me and Ms are the masses of the Earth and the Sun, respectively. Using all the given values, we have \(3.5×10^{22}=(6.7×10^{-11}) \frac{(6×10^{24}×M_e}{(1.5×10^{11})^2}\) ⇒ Ms = \(\frac{(3.5×10^{22})×(1.5×10^{11})^2}{(6.7×10^{-11})×(6×10^{24})}\) Ms = 1.6 X 1030 kg
| View Notes of this Chapter ← Click |
Useful links :
| Main Page : - Maharashtra Board Class 10 Science & Technology Part-1,Part-2 - All chapters notes, solutions, videos, test, pdf.
Books : MSBSHSE -Class 10th Science Text Books – Chapter wise PDF for download Videos : MSBSHSE Class 10th Science & Technology-1-Videos - Chapter wise Videos of all chapter. Next Chapter : Class 10-Sc. & Tech.-1-Chapter-2-Periodic Classification of Element - Online Notes |

the important and man question
lasson explain sir
reply sir
yes, we will try to include it, but it will take some time, thanks for valuable suggestion, stay connected with us.
It’s so good
This is a very good site for practice for kids, if more numericals are added along with the solutions it would be a great practice, Thank you for this site.
yes, we are working for the the same