Motion In a Straight Line
Based on NCERT Class 11th Physics Chapter 3
Theory
Motion: Motion is change in position of an object with time.
Motion of object along a straight line is called rectilinear motion.
Examples include flying kite, moving train, earth’s rotation etc.

Frame of Reference :
In order to know the change in position of an object, a reference point is required. Point O in the figure is the reference point or Origin and together with three axes, this system is called the coordinate system. A coordinate system with time frame is called frame of reference.
- Objects changing positions with time with respect to the frame of reference are in motion while those which do not change position are at rest.
- For a moving car, for the frame of reference outside the car, it appears moving. While for the frame of reference inside the car, the car appears stationary.
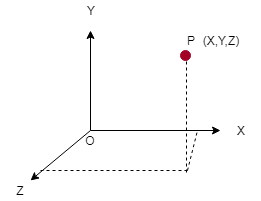
The point of intersection of these three axes is called origin (O) and serves as the reference point.
The coordinates (x, y. z) of an object P describe the position of the object with respect to this coordinate system.
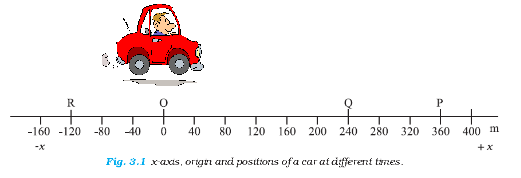
Consider the motion of a car along a straight line. We choose the x-axis such that it coincides with the path of the car’s motion and origin of the axis as the point from where the car started moving, i.e. the car was at x = 0 at t = 0 (Fig. 3.1).
Let P, Q and R represent the positions of the car at different instants of time. Consider two cases of motion.
In the first case, the car moves from O to P. Then the distance moved by the car is OP = +360 m.
This distance is called the path length traversed by the car.
In the second case, the car moves from O to P and then moves back from P to Q.
During this course of motion, the path length traversed is OP + PQ = + 360 m + (+120 m) = + 480 m.
Path length : It is the distance between two points along a straight line. It is a scalar quantity — a quantity that has a magnitude only and no direction
Displacement : It is the change in position in a particular time interval. It is vector quantity. Change is position is usually denoted by Δx (x2- x1) and change in time is denoted by Δt (t2- t1).
Example:
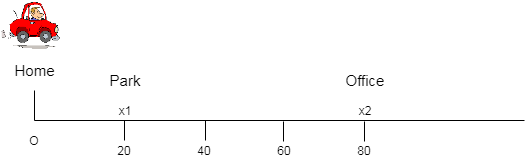
if a Car traveled from home (O) to office (x2) and comes back from office to Park (x1), then
Path length(Home to office and office to Park) = Ox2 + x2x1 = (+80) + (+60) = +140m. This is always positive.
Displacement(Home to Park) = Ox2 - x2x1 = +80 – (+60) = +20m. This can be positive as well as negative. The negative sign indicates the direction.
- Magnitude of Displacement may or may not be equal to the path length.
- For a non-zero path length, displacement can be 0 (case where an object returns to origin).
If an object moving along the straight line covers equal distances in equal intervals of time, it is said to be in uniform motion along a straight line.
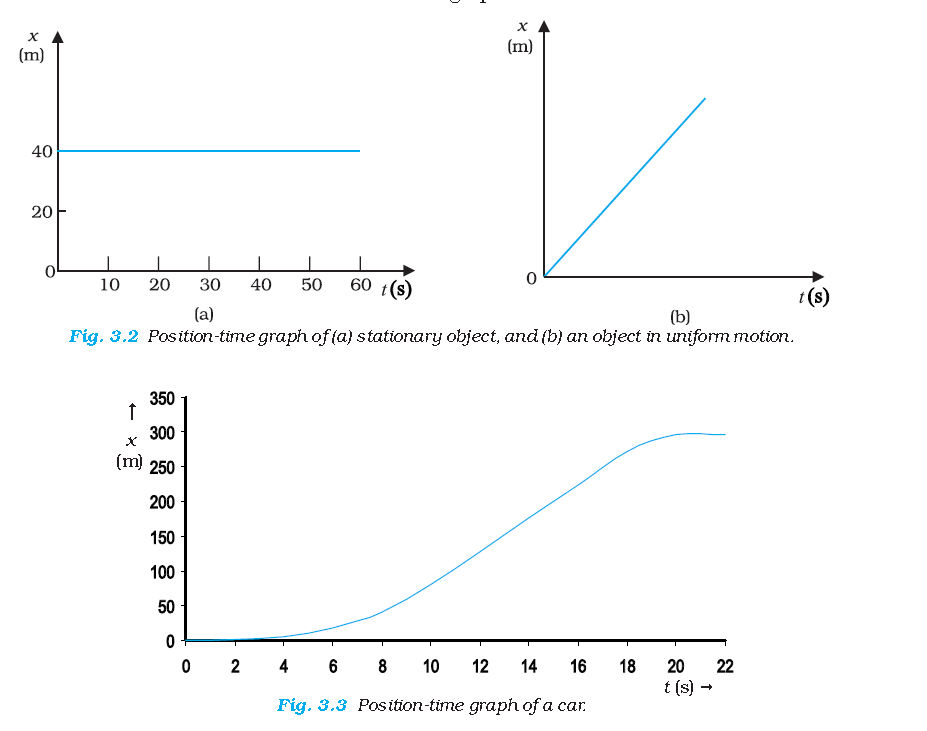
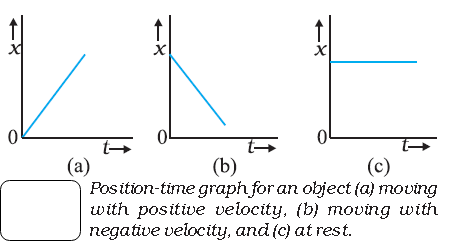
Position-Time, Velocity-Time and Acceleration-Time Graph
| Criteria | P-T Graph | V-T Graph | A-T Graph |
| X and Y axis | Time and Position | Time and Velocity | Time and Acceleration |
| Slope | It represents velocity of an object | It represents acceleration of an object. | It represents the jerk or push of a moving object. |
| Straight slope | Uniform velocity | Uniform acceleration | Uniform jerk |
| Curvy Slope | Change in velocity | Change in acceleration | Change in the amount of push/jerk |
Average velocity : is defined as the change in position or displacement (Δx) divided by the time intervals (Δt), in which the displacement occurs. Like displacement, average velocity is also a vector quantity.
\(\bar ν\) =\(\frac{x_2-x_1}{t_2-t_1}\) =\(\frac{Δx}{Δt}\)
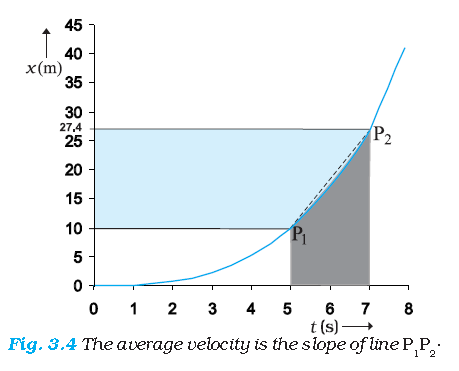
The portion of the x-t graph between t = 0 s and t = 8 s is blown up and shown in Fig. 3.4. As seen from the plot, the average velocity of the car between time t = 5 s and t = 7 s is :
\(\bar ν\) =\(\frac{x_2-x_1}{t_2-t_1}\) =\(\frac{27.4-10}{7-5}\frac{m}{s}\) = 8.7ms-1
Average speed : is defined as the total path length travelled divided by the total time interval during which the motion has taken place :
Average speed = \(\frac{Total\,path\,length}{Total\,time\,interval}\)
Average speed is always positive (in contrast to the average velocity which can be positive or negative).
Example :
(i) A car is moving along a straight line, say OP in Fig. 3.1. It moves from O to P in 18 s and returns from P to Q
in 6.0 s.
What are the average velocity and average speed of the car in going
(a) from O to P ? and
(b) from O to P and back to Q ?

Answer : Average velocity = \(\frac{Displacement}{Time\,interval}\)
\(\bar ν\) = \(\frac{360m}{18s}\) = +20 ms-1
Average speed = \(\frac{Path\, length}{Time\,interval}\)
= \(\frac{360m}{18s}\) = 20 ms-1
Thus, in this case the average speed is equal to the magnitude of the average velocity.
(b) In this case,
Average velocity = \(\frac{Displacement}{Time\,interval}\)
\(\bar ν\) = \(\frac{240m}{(18+6)s}\) = +10 ms-1
Average speed = \(\frac{Path\, length}{Time\,interval}\)
= \(\frac{(360+120)m}{24s}\) = 20 ms-1
Thus, in this case the average speed is not equal to the magnitude of the average velocity.
This happens because the motion here involves change in direction so that the path length is greater than the magnitude of displacement.
This shows that speed is, in general, greater than the magnitude of the velocity.
If the car in Example (i) moves from O to P and comes back to O in the same time interval, average speed is 20 m/s but the average velocity is zero !
Instantaneous Velocity and Instantaneous Speed
Instantaneous velocity: describes how fast an object is moving at different instants of time in a given time interval. It is also defined as average velocity for an infinitely small time interval.
The average velocity tells us how fast an object has been moving over a given time interval but does not tell us how fast it moves at different instants of time during that interval.
The velocity at an instant is defined as the limit of the average velocity as the time interval Δt becomes infinitesimally small.
ν = \(\lim\limits_{x\to\infty}\) \(\frac{Δx}{Δt}\) = \(\frac{dx}{dt}\)
Here lim is taking operation of taking limit with time tending towards 0 or infinitely small.
dx/dt is differential coefficient – Rate of change of position with respect to time at an instant.
We can use above Eq. for obtaining the value of velocity at an instant either graphically or numerically.
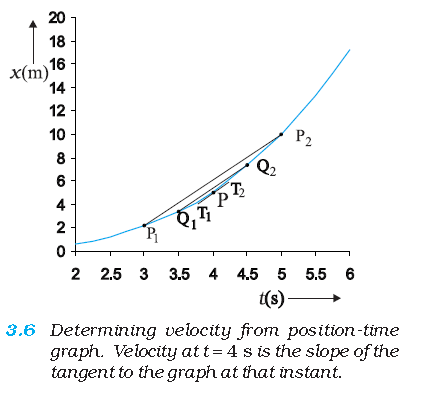
By the definition of the average velocity, the slope of line P1P2 ( Fig. 3.6) gives the value of average velocity over the interval 3 s to 5 s.
Now, we decrease the value of Δt from 2 s to 1 s. Then line P1P2 becomes Q1Q2 and its slope gives the value of the average velocity over the interval 3.5 s to 4.5 s.
**The graphical method for the determination of the instantaneous velocity is always not a convenient method.
Instantaneous speed : is the magnitude of velocity.
Instantaneous speed at an instant is equal to the magnitude of the instantaneous velocity at that instant.
Example : A velocity of + 24.0 m s–1 and a velocity of – 24.0 m s–1 — both have an associated speed of 24.0 m s-1.
Solved Example:
The position of an object moving along x-axis is given by x = a + bt2 where a = 8.5 m, b = 2.5 m s–2 and t is
measured in seconds.
What is its velocity at t = 0 s and t = 2.0 s. ?
What is the average velocity between t = 2.0 s and t = 4.0 s ?
Answer :
In notation of differential calculus, the velocity is
ν = \(\frac{dx}{dt}\) = \(\frac{d}{dt}\) (a + bt2 )= 2b t =2 × 2.5 × t = 5t m s–1
At t = 0 s, v = 0 m s–1 and at t = 2.0 s, v = 10 m s-1 .
Average velocity between t = 2.0 s and t = 4.0 s is :
Average velocity = \(\frac{dx}{dt}\)
= \(\frac{x_2-x_1}{t_2-t_1}\)
= \(\frac{(a+b4^2) -(a +b2^2)}{(4-2)}\)
= \(\frac{12b}{2}\) = 6 × b
= 6 x 2.5 = 15 m s-1 .
Acceleration
Acceleration is rate of change of velocity with time. It is denoted by ‘a’ and the SI unit is m/s2.
Average acceleration is change of velocity over a time interval.
\(\bar a\) = \(\frac{v_2-v_1}{t_2-t_1}\) = \(\frac{Δv}{Δt}\)
Here v1 and v2 are instantaneous velocities at time t1 and t2.
- Acceleration can be positive (increasing velocity) or negative (decreasing velocity).
- Instantaneous acceleration is acceleration at different instants of time. Acceleration at an instant is slope of tangent to the v-t curve at that instant.
a = \(\lim\limits_{Δt\to 0}\) = \(\frac{dv}{dt}\)
Acceleration, may result from a change in speed (magnitude), a change in direction or changes in both. Like velocity, acceleration can also be positive, negative or zero.
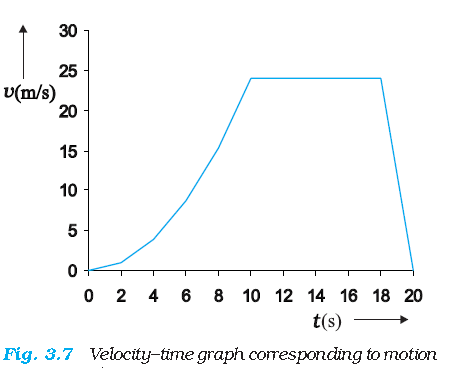
The average acceleration for velocity-time graph shown in Fig. 3.7 for different time intervals 0 s - 10 s, 10 s – 18 s,
and 18 s – 20 s are :
0 s - 10 s = \(\bar a\) = \(\frac{(24-0)ms^{-1}}{(10-0)s}\) = 2.4 ms-2
10 s - 18 s = \(\bar a\) = \(\frac{(24-24)ms^{-1}}{(18-10)s}\) = 0 ms-2
18 s - 20 s = \(\bar a\) = \(\frac{(0-24)ms^{-1}}{(20-18)s}\) = -12 ms-2
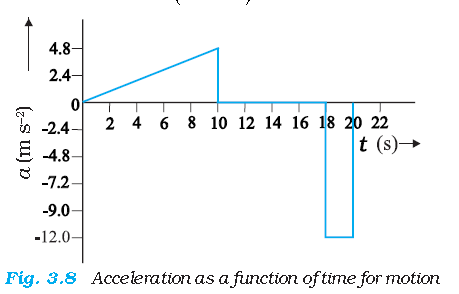
Instantaneous acceleration is defined in the same way as the instantaneous velocity :
The acceleration at an instant is the slope of the tangent to the v–t curve at that instant.
For the v–t curve shown in Fig. 3.7, we can obtain acceleration at every instant of time. The resulting a – t curve is shown in Fig. 3.8
An interesting feature of a velocity-time graph for any moving object is that the area under the curve represents the displacement over a given time interval.
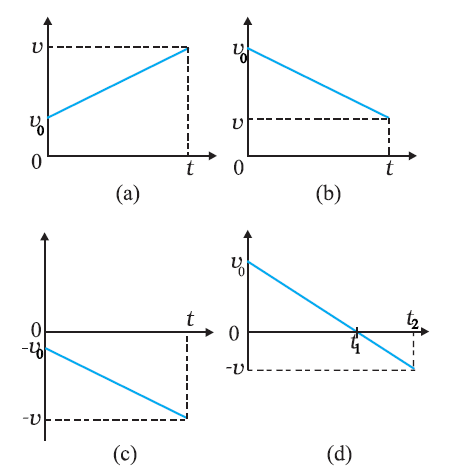
Velocity–time graph for motions with constant acceleration.
(a) Motion in positive direction with positive acceleration,
(b) Motion in positive direction with negative acceleration,
(c) Motion in negative direction with negative acceleration,
(d) Motion of an object with negative acceleration that changes direction at time t1. Between times 0 to t1, its moves in positive x - direction and between t1 and t2 it moves in the opposite direction.
Acceleration and velocity cannot change values abruptly at an instant. Changes are always continuous.
There are 3 kinematic equations of rectilinear motion for constant acceleration
| Position of object at time t=0 is 0 | Position of object at time t=0 is x0 |
| v = v0 + at | v = v0 + at |
| x = v0t + ½ at2 | x = x0+ v0t + ½ at2 |
| v2 = v02 + 2ax | v2 = v02 + 2a(x-x0) |
The area under this curve is : Area between instants 0 and t = Area of triangle ABC + Area of rectangle OACD
= \(\frac{1}{2}\) (v-v0 )t + v0 t
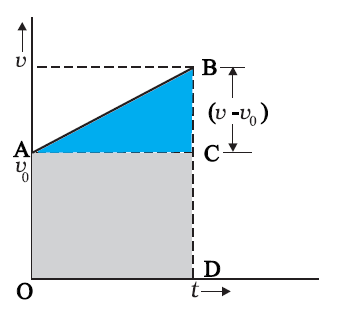
Area under v-t curve for an object with uniform acceleration
Relative Velocity :
This is the velocity of an object relative to some other object which might be stationary, moving slowly, moving with same velocity, moving with higher velocity or moving in opposite direction.
If initial position of two objects A and B are xA (0) and xB (0), the position at time t will be,
- xA (t) = xA (0) + vA t
- xB (t) = xB (0) + vB t
- Displacement from object A to B, [ xB (0) - xA (0) ] + (vB -vA)t
- Velocity of B relative to A = vBA = vB – vA
- Velocity of A relative to B = vAB = vA – vB
Position-time graphs of two objects with equal velocities.
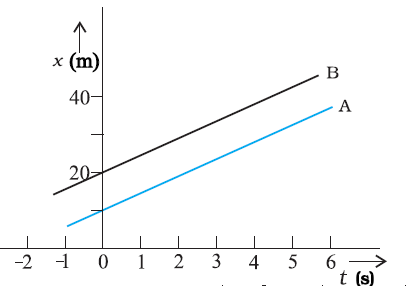
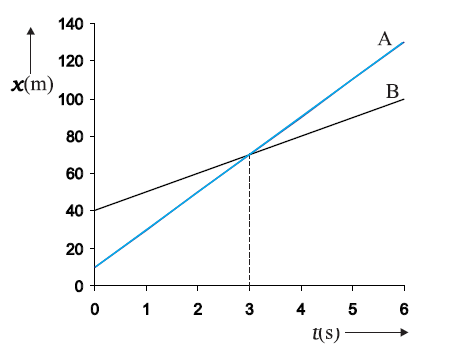
Position-time graphs of two objects with unequal velocities, showing the time of meeting
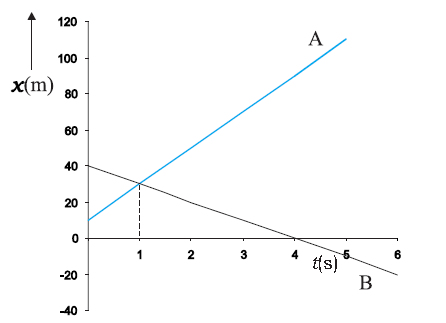
Position-time graphs of two objects with velocities in opposite directions, showing the time of meeting
Example :
(i) Obtain equations of motion for constant acceleration using method of calculus.
Answer : By definition
a= \(\frac{dv}{dt}\)
dv = a dt
Integrating both sides
\(\int_{v_0}^{v}dv\) = \(\int_{0}^{t} a \, dt\)
= \(a\int_{0}^{t} dt\) ......(a is constant)
v-v0 = at
v = v0 + at
Further, v= \(\frac{dx}{dt}\)
dx = v dt
Integrating both sides
\(\int_{x_0}^{x}dv\) = \(\int_{0}^{t} v \, dt\)
= \(\int_{0}^{t} (v_0 + at) dt\)
x - x0 = v0t + (1/2)at2
x = x0 + v0t + (1/2)at2
We can write
a = \(\frac{dv}{dt}\) = \(\frac{dv}{dx}\) \(\frac{dx}{dt}\) = \(v\frac{dv}{dx}\)
or \(vdv\) =\( adx\)
Integrating both sides,
\(\int_{v_0}^{v}t\,dv\) = \(\int_{x_0}^{x}adx\)
\(v-{v_0}^2 \over 2\) = \(a(x-x_0)\)
\(v^2\) = \({v_0}^2 + 2a(x-x_0)\)
The advantage of this method is that it can be used for motion with non-uniform acceleration also.
(ii) A ball is thrown vertically upwards with a velocity of 20 m s–1 from the top of a multistorey building.
The height of the point from where the ball is thrown is 25.0 m from the ground.
(a) How high will the ball rise ?
(b) how long will it be before the ball hits the ground?
Take g = 10 m s–2.
Answer :
(a) Let us take the y-axis in the vertically upward direction with zero at the ground, as shown in Fig.
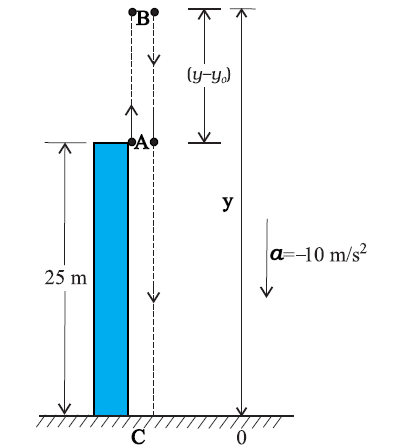
Now vo = + 20 m s–1,
a = – g = –10 m s–2,
v = 0 m s–1
If the ball rises to height y from the point of launch, then using the equation
\(v^2\) = \({v_0}^2 + 2a (y-y_0)\)
we get
0 = (20)2 + 2(–10)(y – y0)
Solving, we get, (y – y0) = 20 m.
(b) using equation.
\(y\) = \(y_0 + v_0t + \frac{1}{2}at^2\)
Now \(y_0\) = 25 m, y = 0 m, \(v_o\) = 20 m s-1, a = –10m s–2, t = ?
0 = 25 +20 t + (½) (-10) t2
Or, 5t2 – 20t – 25 = 0
Solving this quadratic equation for t, we get
t = 5s
(iii) Free-fall : Discuss the motion of an object under free fall. Neglect air resistance.
Answer : An object released near the surface of the Earth is accelerated downward under the influence of the force of gravity.
The magnitude of acceleration due to gravity is represented by g. If air resistance is neglected, the object is
said to be in free fall.
If the height through which the object falls is small compared to the earth’s radius, g can be taken to be constant,
equal to 9.8 m s–2.
Free fall is thus a case of motion with uniform acceleration.
We assume that the motion is in y-direction, more correctly in –y-direction because we choose upward direction as positive.
Since the acceleration due to gravity is always downward, it is in the negative direction and we have
a = – g = – 9.8 m s–2
The object is released from rest at y = 0.
Therefore, v0 = 0 and the equations of motion become:
v = 0 – g t = –9.8 t m s–1
y = 0 – ½ g t2 = –4.9 t 2 m
v2 = 0 – 2 g y = –19.6 y m2 s–2
These equations give the velocity and the distance travelled as a function of time and also the variation of velocity with distance.
The variation of acceleration, velocity, and distance, with time have been plotted in Fig. (a), (b) and (c).
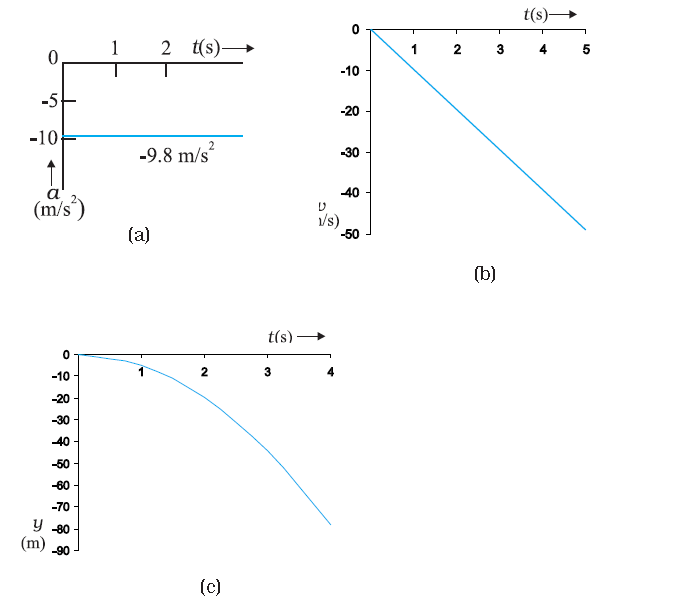
Motion of an object under free fall.
(a) Variation of acceleration with time.
(b) Variation of velocity with time.
(c) Variation of distance with time
(iv) Galileo’s law of odd numbers :
“The distances traversed, during equal intervals of time, by a body falling from rest, stand to one another in the same ratio as the odd numbers beginning with unity [namely, 1: 3: 5: 7…...].” Prove it.
Answer : Let us divide the time interval of motion of an object under free fall into many ual intervals τ and find out the distances traversed during successive intervals of time.
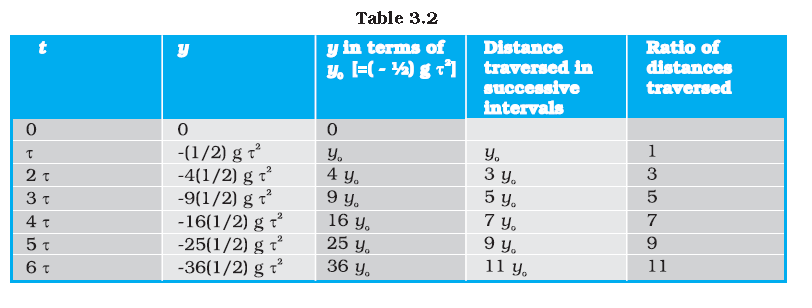
y= -(1/2)gt2
Using this equation, we can calculate the position of the object after different time intervals, 0, τ, 2τ, 3τ… which are given in second column of Table 3.2.
If we take y0 = (–1/2) gτ2
the position coordinate after first time interval τ, then third column gives the positions in the unit of yo.
The fourth column gives the distances traversed in successive τs.
We find that the distances are in the simple ratio 1: 3: 5: 7: 9: 11… as shown in the last column. This law was established by Galileo Galilei (1564-1642) who was the first to make quantitative studies of free fall.
(v) Stopping distance of vehicles :
When brakes are applied to a moving vehicle, the distance it travels before stopping is called stopping distance.
It is an important factor for road safety and depends on the initial velocity (v0) and the braking capacity, or deceleration, –a that is caused by the braking.
Derive an expression for stopping distance of a vehicle in terms of vo and a.
Answer : Let the distance travelled by the vehicle before it stops be ds.
Then, using equation of motion v2 = vo 2 + 2 ax, and noting that v = 0, we have the stopping distance
Thus, the stopping distance is proportional to the square of the initial velocity. Doubling the initial velocity increases the stopping distance by a factor of 4 (for the same deceleration).
For the car of a particular make, the braking distance was found to be 10 m, 20 m, 34 m and 50 m corresponding to velocities of 11, 15, 20 and 25 m/s which are nearly consistent with the above formula.
Stopping distance is an important factor considered in setting speed limits, for example, in school zones.
(vi) Reaction time : When a situation demands our immediate action, it takes some time before we really respond. Reaction time is the time a person takes to observe, think and act.
For example, if a person is driving and suddenly a boy appears on the road, then the time elapsed before he slams the brakes of the car is the reaction time.
Reaction time depends on complexity of the situation and on an individual.
You can measure your reaction time by a simple experiment. Take a ruler and ask your friend to drop it vertically
through the gap between your thumb and forefinger (Fig.). After you catch it, find the distance d travelled by the ruler. In a particular case, d was found to be 21.0 cm. Estimate reaction time.
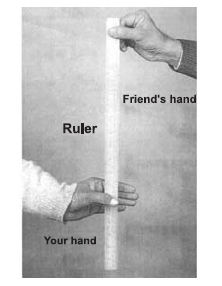
Answer : The ruler drops under free fall.
Therefore, vo = 0, and g = –9.8 m s–2.
The distance travelled d and the reaction time tr are related by
d= -\(\frac{1}{2}\) \(g{t_r}^2\)
∴\(t_r\) = \(\sqrt{2d \over g}\)s
Given d = 21.0 cm and g = 9.8 m s–2 the reaction time is
\(t_r\) = \(\sqrt{2 × 21 \over 9.8}\)s ≅ 0.2 s
(vii)Two parallel rail tracks run north-south. Train A moves north with a speed of 54 km h–1, and train B moves south with a speed of 90 km h–1.
What is the (a) velocity of B with respect to A ?,
(b) velocity of ground with respect to B ?,
and
(c) velocity of a monkey running on the roof of the train A against its motion (with a velocity of 18 km h–1 with
respect to the train A) as observed by a man standing on the ground ?
Answer : Choose the positive direction of x-axis to be from south to north. Then,
vA = + 54 km h–1 = 15 m s–1
vB = – 90 km h–1 = – 25 m s–1
Relative velocity of B with respect to A = vB – vA= (-25-15) = – 40 m s–1 , i.e. the train B appears to A to move
with a speed of 40 m s–1from north to south.
Relative velocity of ground with respect to B = 0 – vB = 25 m s–1. ....... ( Velocity of ground =0)
In (c), let the velocity of the monkey with respect to ground be vM. Relative velocity of the monkey
with respect to A,
vMA = vM – vA = –18 km h–1 = 18 x 1000/60 x 60 = –5 ms–1.
Therefore, vM = vMA + vA = (-5 + 15) m s–1 = 10 m s–1.