Sets
Based on NCERT Class 11th Mathematics Chapter 1
Notes
| NCERT - Class 11 Mathematics Chapter 1 Sets Notes |
Topics : Sets and their representations. Empty set. Finite and Infinite sets. Equal sets. Subsets. Subsets of a set of real numbers especially intervals (with notations). Power set. Universal set. Venn diagrams. Union and Intersection of sets. Difference of sets. Complement of a set. Properties of Complement.
A set is a well-defined collection of objects.
Sets used particularly in mathematics, viz.
- N : the set of all natural numbers
- Z : the set of all integers
- Q : the set of all rational numbers
- R : the set of real numbers
- Z+ : the set of positive integers
- Q+ : the set of positive rational numbers
- R+ : the set of positive real numbers.
The following points may be noted :
(i) Objects, elements and members of a set are synonymous terms.
(ii) Sets are usually denoted by capital letters A, B, C, X, Y, Z, etc.
(iii) The elements of a set are represented by small letters a, b, c, x, y, z, etc.
If a is an element of a set A, we say that “ a belongs to A” the Greek symbol ∈ (epsilon) is used to denote the phrase ‘belongs to’. Thus, we write a ∈ A.
If ‘b’ is not an element of a set A, we write b ∉ A and read “b does not belong to A”.
Thus, in the set V of vowels in the English alphabet, a ∈ V but b ∉ V.
In the set P of prime factors of 30, 3 ∈ P but 15 ∉ P.
There are two methods of representing a set :
(i) Roster or tabular form : In roster form, all the elements of a set are listed, the elements are being separated
by commas and are enclosed within braces { }.
- In roster form, the order in which the elements are listed is immaterial.
- It may be noted that while writing the set in roster form an element is not generally repeated, i.e., all the elements are taken as distinct.
Example:
1-The set of all even positive integers less than 7 is described in roster form as {2, 4, 6}.
2-The set of all natural numbers which divide 42 is {1, 2, 3, 6, 7, 14, 21, 42}. OR {1, 3, 7, 21, 2, 6, 14, 42}.
3-The set of all vowels in the English alphabet is {a, e, i, o, u}.
4-The set of odd natural numbers is represented by {1, 3, 5, . . .}. The dots tell us that the list of odd numbers continue indefinitely.
5-The set of letters forming the word ‘SCHOOL’ is { S, C, H, O, L} or {H, O, L, C, S}. Here, the order of listing elements has no relevance.
(ii) Set-builder form: In set-builder form, all the elements of a set possess a single common property
which is not possessed by any element outside the set.
In set-builder form we describe the element of the set by using a symbol x (any other symbol like the letters y, z, etc. could be used) which is followed by a colon “ : ”. After the sign of colon, we write the characteristic property possessed by the elements of the set and then enclose the whole description within braces.
Example:
1- In the set {a, e, i, o, u}, all the elements possess a common property, namely, each of them is a vowel in the English alphabet, and no other letter possess this property.
Denoting this set by V, we write
V = {x : x is a vowel in English alphabet}
Description of the set V is read as “the set of all x such that x is a vowel of the English alphabet”.
In this description the braces stand for “the set of all”, the colon stands for “such that”.
2- A = {x : x is a natural number and 3 < x < 10}
is read as “the set of all x such that x is a natural number and x lies between 3 and 10.”
Hence, the numbers 4, 5, 6, 7, 8 and 9 are the elements of the set A.
3- A= {x : x is a natural number which divides 42}
4- B= {y : y is a vowel in the English alphabet}
5- C= {z : z is an odd natural number}
The Empty Set : A set which does not contain any element is called the empty set or the null set or the void set.
The empty set is denoted by the symbol Φ or { }.
Examples of empty sets :
(i) Let A = {x : 1 < x < 2, x is a natural number}. Then A is the empty set,
because there is no natural number between 1 and 2.
(ii) B = {x : x2 – 2 = 0 and x is rational number}. Then B is the empty set
because the equation x2 – 2 = 0 is not satisfied by any rational value of x.
(iii) C = {x : x is an even prime number greater than 2}. Then C is the empty set,
because 2 is the only even prime number.
(iv) D = { x : x2 = 4, x is odd }. Then D is the empty set,
because the equation x2 = 4 is not satisfied by any odd value of x.
Finite and Infinite Sets : A set which is empty or consists of a definite number of elements is called finite otherwise, the set is called infinite.
It is not possible to write all the elements of an infinite set within braces { } because the numbers of elements of such a set is not finite. So, we represent some infinite set in the roster form by writing a few elements which clearly indicate the structure of the set followed ( or preceded ) by three dots. Ex-{1,2,3,4....}
Note: All infinite sets cannot be described in the roster form. For example, the set of real numbers cannot be described in this form, because the elements of this set do not follow any particular pattern.
Example :
State which of the following sets are finite or infinite :
(i) {x : x ∈ N and (x – 1) (x –2) = 0} - Answer: Given set = {1, 2}. Hence, it is finite.
(ii) {x : x ∈ N and x2 = 4} - Answer: Given set = {2}. Hence, it is finite.
(iii) {x : x ∈ N and 2x –1 = 0} - Answer: Given set = f. Hence, it is finite.
(iv) {x : x ∈ N and x is prime} - Answer: The given set is the set of all prime numbers and since set of prime
numbers is infinite. Hence the given set is infinite
(v) {x : x ∈ N and x is odd} - Answer : Since there are infinite number of odd numbers, hence, the given set is
infinite.
Equal Sets : Two sets A and B are said to be equal if they have exactly the same elements and we write A = B. Otherwise, the sets are said to be unequal and we write A ≠ B.
Note : A set does not change if one or more elements of the set are repeated.
For example, the sets A = {1, 2, 3} and B = {2, 2, 1, 3, 3} are equal, since each element of A is in B and vice-versa. That is why we generally do not repeat any element in describing a set.
Examples :
(i) Let A = {1, 2, 3, 4} and B = {3, 1, 4, 2}. Then A = B.
(ii) Let A be the set of prime numbers less than 6 and P the set of prime factors of 30. Then A and P are equal, since 2, 3 and 5 are the only prime factors of 30 and also these are less than 6.
(iii) Find the pairs of equal sets, if any, give reasons:
A = {0}, B = {x : x > 15 and x < 5}, C = {x : x – 5 = 0 }, D = {x: x2 = 25}, E = {x : x is an integral positive root of the equation x2 – 2x –15 = 0}.
Solution: Since 0 ∈ A and 0 does not belong to any of the sets B, C, D and E, it follows that, A ≠ B, A ≠ C, A ≠ D, A ≠ E.
Since B = Φ but none of the other sets are empty. Therefore B ≠ C, B ≠ D and B ≠ E.
Also C = {5} but –5 ∈ D, hence C ≠ D.
Since E = {5}, C = E.
Further, D = {–5, 5} and E = {5}, we find that, D ≠ E.
Thus, the only pair of equal sets is C and E.
Subsets : A set A is said to be a subset of a set B if every element of A is also an element of B.
| Example : Consider the sets : X = set of all students in your school, Y = set of all students in your class. We note that every element of Y is also an element of X; we say that Y is a subset of X. The fact that Y is subset of X is expressed in symbols as Y ⊂ X. The symbol ⊂ stands for ‘is a subset of’ or ‘is contained in’. |
A ⊂ B if whenever a∈ A, then a ∈ B. It is often convenient to
use the symbol “⇒” which means implies. Using this symbol, we can write the definition of subset as follows:
A ⊂ B if a ∈ A ⇒ a ∈ B
We read the above statement as “A is a subset of B if 'a' is an element of A implies that 'a' is also an element of B”. If A is not a subset of B, we write A ⊄ B.
We may note that for A to be a subset of B, all that is needed is that every element of A is in B.
It is possible that every element of B may or may not be in A. If it so happens that every element of B is also in A, then we shall also have B ⊂ A. In this case, A and B are the same sets so that we have A ⊂ B and B ⊂ A ⇔ A = B,
where “⇔” is a symbol for two way implications, and is usually read as if and only if (briefly written as “iff”).
It follows from the above definition that every set A is a subset of itself, i.e., A ⊂ A.
Since the empty set Φ has no elements, we agree to say that Φ is a subset of every set
Examples :
(i) The set Q of rational numbers is a subset of the set R of real numbes, and we write Q ⊂ R.
(ii) If A is the set of all divisors of 56 and B the set of all prime divisors of 56, then B is a subset of A and we write B ⊂ A.
(iii) Let A = {1, 3, 5} and B = {x : x is an odd natural number less than 6}. Then A ⊂ B and B ⊂ A and hence A = B.
(iv) Let A = { a, e, i, o, u} and B = { a, b, c, d}. Then A is not a subset of B, also B is not a subset of A.
Let A and B be two sets. If A ⊂ B and A ≠ B , then A is called a proper subset of B and B is called superset of A. For example, A = {1, 2, 3} is a proper subset of B = {1, 2, 3, 4}.
If a set A has only one element, we call it a singleton set. Thus,{ a } is a singleton set.
Subsets of set of real numbers :
there are many important subsets of R. We give below the names of some of these subsets.
The set of natural numbers N = {1, 2, 3, 4, 5, . . .}
The set of integers Z = {. . ., –3, –2, –1, 0, 1, 2, 3, . . .}
The set of rational numbers Q = { x : x = \(\frac{p}{ q}\), p, q ∈ Z and q ≠ 0}
The set of irrational numbers, denoted by T, is composed of all other real numbers.
Thus T = {x : x ∈ R and x ∉ Q}, i.e., all real numbers that are not rational. Members of T include √2 , √5 and π .
Some of the obvious relations among these subsets are:
N ⊂ Z ⊂ Q, Q ⊂ R, T ⊂ R, N ⊄ T.
Intervals as subsets of R : Let a, b ∈ R and a < b. Then the set of real numbers { y : a < y < b} is called an open interval and is denoted by (a, b). All the points between 'a' and 'b' belong to the open interval (a, b) but a, b themselves do not belong to this interval.
The interval which contains the end points also is called closed interval and is denoted by [ a, b ].
Thus [ a, b ] = {x : a ≤ x ≤ b}
We can also have intervals closed at one end and open at the other, i.e.,
[ a, b ) = {x : a ≤ x < b} is an open interval from a to b, including a but excluding b.
( a, b ] = { x : a < x ≤ b } is an open interval from a to b including b but excluding a.
Example: If A = (–3, 5) and B = [–7, 9], then A ⊂ B.
The set [ 0, ∞) defines the set of non-negative real numbers,
while set ( – ∞, 0 ) defines the set of negative real numbers. The set ( – ∞, ∞ ) describes the set of real numbers in relation to a line extending from – ∞ to ∞ .
Example : The set {x : x ∈ R, –5 < x ≤ 7}, written in set-builder form, can be written in the form of interval as (–5, 7] and the interval [–3, 5) can be written in set builder form as {x : –3 ≤ x < 5}.
The number (b – a) is called the length of any of the intervals (a, b), [a, b], [a, b) or (a, b].
Power Set : The collection of all subsets of a set A is called the power set of A. It is denoted by P(A). In P(A), every element is a set.
Consider the set {1, 2}. Let us write down all the subsets of the set {1, 2}.
We know that Φ is a subset of every set . So, Φ is a subset of {1, 2}.
We see that {1} and { 2 }are also subsets of {1, 2}.
Also, we know that every set is a subset of itself. So, { 1, 2 } is a subset of {1, 2}.
Thus, the set { 1, 2 } has, in all, four subsets, viz. Φ, { 1 }, { 2 } and { 1, 2 }. The set of all these subsets is called the
power set of { 1, 2 }.
Thus, as in above, if A = { 1, 2 }, then P( A ) = { Φ,{ 1 }, { 2 }, { 1,2 }}
Also, note that n [ P (A) ] = 4 = 22 (n=numbers of element)
In general, if A is a set with n(A) = m, then it can be shown that n [ P(A)] = 2m.
Universal Set : The universal set is usually denoted by U, and all its subsets by the letters A, B, C, etc.
Example :
(i) For the set of all integers, the universal set can be the set of rational numbers or, for that matter, the set R of real numbers.
(ii) In human population studies, the universal set consists of all the people in the world.
Venn Diagrams : Most of the relationships between sets can be represented by means of diagrams which are known as Venn diagrams.
These diagrams consist of rectangles and closed curves usually circles.
The universal set is represented usually by a rectangle and its subsets by circles.
In Venn diagrams, the elements of the sets are written in their respective circles (Figs)
 |
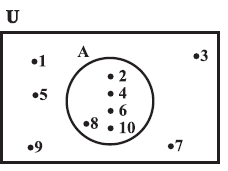| In Fig U = {1,2,3, ..., 10} is the universal set of which A = {2,4,6,8,10} is a subset. |
 |
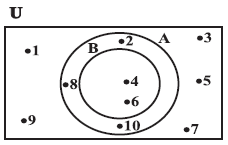| In Fig 1.3, U = {1,2,3, ..., 10} is the universal set of which A = {2,4,6,8,10} and B = {4, 6} are subsets, and also B ⊂ A |
The reader will see an extensive use of the Venn diagrams when we discuss the union, intersection and difference of sets.
Operations on Sets : There are some operations which when performed on two sets give rise to another set.
We will now define certain operations on sets and examine their properties. Henceforth, we will refer all our sets as subsets of some universal set.
Union of sets : Let A and B be any two sets. The union of A and B is the set which consists of all the elements of A and all the elements of B, the common elements being taken only once.
The symbol ‘∪’ is used to denote the union. Symbolically, we write A ∪ B and usually read as ‘A union B’.
Example:
(i) Let A = { 2, 4, 6, 8} and B = { 6, 8, 10, 12}. Find A ∪ B.
Solution : We have A ∪ B = { 2, 4, 6, 8, 10, 12}
Note that the common elements 6 and 8 have been taken only once while writing A ∪ B.
(ii) Let A = { a, e, i, o, u } and B = { a, i, u }. Show that A ∪ B = A
Solution : We have, A ∪ B = { a, e, i, o, u } = A.
This example illustrates that union of sets A and its subset B is the set A itself, i.e., if B ⊂ A, then A ∪ B = A.
(ii) Let X = {Ram, Geeta, Akbar} be the set of students of Class XI, who are in school hockey team.
Let Y = {Geeta, David, Ashok} be the set of students from Class XI who are in the school football team.
Find X ∪ Y and interpret the set.
Solution : We have, X ∪ Y = {Ram, Geeta, Akbar, David, Ashok}. This is the set of students from Class XI who are in the hockey team or the football team or both.
Thus, we can define the union of two sets as follows:
 |
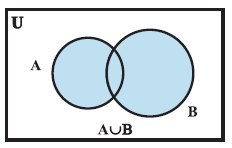| The union of two sets A and B is the set C which consists of all those elements which are either in A or in B (including those which are in both). In symbols, we write. A ∪ B = { x : x ∈A or x ∈ B } The union of two sets can be represented by a Venn diagram as shown in Fig . The shaded portion in Fig represents A ∪ B |
Properties of the Operation of Union :
(i) A ∪ B = B ∪ A - (Commutative law)
(ii) ( A ∪ B ) ∪ C = A ∪ ( B ∪ C) - (Associative law )
(iii) A ∪ Φ = A - (Law of identity element, Φ is the identity of ∪)
(iv) A ∪ A = A - (Idempotent law)
(v) U ∪ A = U (Law of U)
Intersection of sets : The intersection of sets A and B is the set of all elements which are common to both A and B. The symbol ‘∩’ is used to denote the intersection.
The intersection of two sets A and B is the set of all those elements which belong to both A and B.
Symbolically, we write A ∩ B = {x : x ∈ A and x ∈ B}.
 |
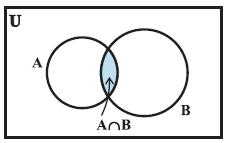| The shaded portion in Fig indicates the intersection of A and B. |
 |
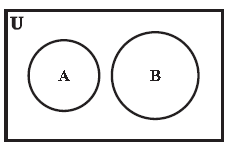| If A and B are two sets such that A ∩ B = Φ, then A and B are called disjoint sets. |
Properties of Operation of Intersection :
(i) A ∩ B = B ∩ A (Commutative law).
(ii) ( A ∩ B ) ∩ C = A ∩ ( B ∩ C ) (Associative law).
(iii) Φ ∩ A = Φ, U ∩ A = A (Law of Φ and U).
(iv) A ∩ A = A (Idempotent law)
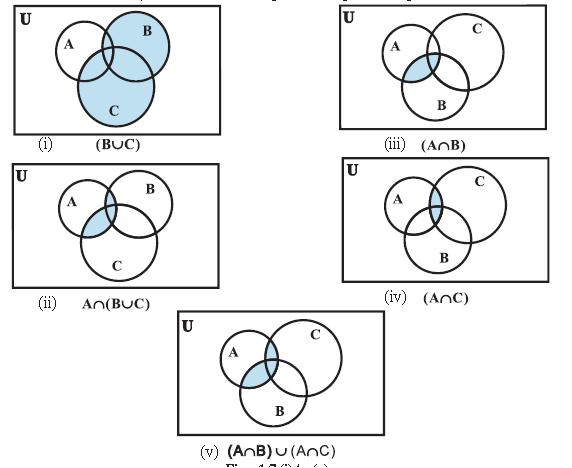
(v) A ∩ ( B ∪ C ) = ( A ∩ B ) ∪ ( A ∩ C ) (Distributive law ) i. e., ∩ distributes over ∪
This can be seen easily from the following Venn diagrams
Difference of sets: The difference of the sets A and B in this order is the set of elements which belong to A but not to B. Symbolically, we write A – B and read as “ A minus B”.
Example:
(i) Let A = { 1, 2, 3, 4, 5, 6}, B = { 2, 4, 6, 8 }. Find A – B and B – A.
Solution : We have, A – B = { 1, 3, 5 }, since the elements 1, 3, 5 belong to A but not to B and
B – A = { 8 }, since the element 8 belongs to B and not to A.
We note that A – B ≠B – A.
(ii) Let V = { a, e, i, o, u } and B = { a, i, k, u}. Find V – B and B – V
Solution : We have, V – B = { e, o }, since the elements e, o belong to V but not to B
and B – V = { k }, since the element k belongs to B but not to V.
We note that V – B ≠ B – V. Using the set builder notation, we can rewrite the definition of difference as
A – B = { x : x ∈ A and x ∉ B }
 |
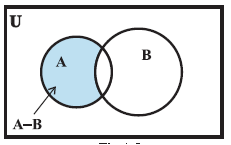| The difference of two sets A and B can be represented by Venn diagram as shown in Fig The shaded portion represents the difference of the two sets A and B |
 |
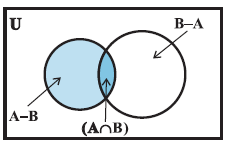| Remark : The sets A – B, A ∩ B and B – A are mutually disjoint sets, i.e., the intersection of any of these two sets is the null set as shown in Fig |
Complement of a Set :
Let U be the universal set and A is a subset of U. Then the complement of A is the set of all elements of U which are not the elements of A. Symbolically, we write A' to denote the complement of A with respect to U.
Thus, A' = {x : x ∈ U and x ∉ A }. Obviously A' = U – A
We note that the complement of a set A can be looked upon, alternatively, as the difference between a universal set U and the set A.
Example:
(i) Let U = {1, 2, 3, 4, 5, 6, 7, 8, 9, 10} and A = {1, 3, 5, 7, 9}. Find A'.
Solution : We note that 2, 4, 6, 8, 10 are the only elements of U which do not belong to A.
Hence A' = { 2, 4, 6, 8,10 }.
Note : If A is a subset of the universal set U, then complement of A' is also a subset of U.
in Example above, we have A' = { 2, 4, 6, 8, 10 }
Hence (A' )'= {x : x ∈ U and x ∉ A'} = {1, 3, 5, 7, 9} = A
It is clear from the definition of the complement that for any subset of the universal set U, we have ( A' )' = A
(ii) Let U be universal set of all the students of Class XI of a coeducational school and A be the set of all girls in Class XI. Find A'.
Solution: Since A is the set of all girls, A' is clearly the set of all boys in the class.
Let find the results for ( A ∪ B )' and A' ∩ B' in the following example.
Example : Let U = {1, 2, 3, 4, 5, 6}, A = {2, 3} and B = {3, 4, 5}. Find A', B' , A' ∩ B', A ∪ B and hence show that ( A ∪ B )' = A' ∩ B'.
Solution : Clearly A' = {1, 4, 5, 6}, B' = { 1, 2, 6 }. Hence A' ∩ B' = { 1, 6 }
Also A ∪ B = { 2, 3, 4, 5 }, so that (A ∪ B)' = { 1, 6 }
( A ∪ B )' = { 1, 6 } = A' ∩ B'
It can be shown that the above result is true in general. If A and B are any two subsets of the universal set U, then
( A ∪ B )' = A' ∩ B'. Similarly, ( A ∩ B )' = A' ∪ B' . These two results are stated in words as follows :
| The complement of the union of two sets is the intersection of their complements and the complement of the intersection of two sets is the union of their complements. These are called De Morgan’s laws.
The complement A¢ of a set A can be represented by a Venn diagram as shown in Fig The shaded portion represents the complement of the set A. |
Properties of Complement Sets :
1. Complement laws:
(i) A ∪ A' = U
(ii) A ∩ A' = Φ
2. De Morgan’s law:
(i) (A ∪ B)´ = A' ∩ B'
(ii) (A ∩ B)' = A' ∪ B'
3. Law of double complementation : (A' )' = A
4. Laws of empty set and universal set Φ' = U and U' = Φ. These laws can be verified by using Venn diagrams.
Practical problems related to our daily life.
The formulae derived in this Section will also be used in subsequent Chapter on Probability (Chapter 16).
Let A and B be finite sets.
(i) If A ∩ B = Φ, then (i) n ( A ∪ B ) = n ( A ) + n ( B ) ... (1)
The elements in A ∪ B are either in A or in B but not in both as A ∩ B = Φ. So, (1) follows immediately.
(ii) If A and B are finite sets, then (ii) n ( A ∪ B ) = n ( A ) + n ( B ) – n ( A ∩ B ) ... (2)
 |
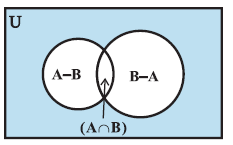| The sets A – B, A ∩ B and B – A are disjoint and their union is A ∪ B (Fig ). |
Therefore
n ( A ∪ B) = n ( A – B) + n ( A ∩ B ) + n ( B – A )
= n ( A – B) + n ( A ∩ B ) + n ( B – A ) + n ( A ∩ B ) – n ( A ∩ B) ....... (add and subtract n ( A ∩ B ) )
But n ( A – B) + n ( A ∩ B ) = n ( A ) and n ( B – A ) + n ( A ∩ B ) = n ( B ) .... ref fig.
∴ n ( A ∪ B) = n ( A ) + n ( B ) – n ( A ∩ B), which verifies (2)
(iii) If A, B and C are finite sets, then
n ( A ∪ B ∪ C ) = n ( A ) + n ( B ) + n ( C ) – n ( A ∩ B ) – n ( B ∩ C) – n ( A ∩ C ) + n ( A ∩ B ∩ C ) ... (3)
we have
n ( A ∪ B ∪ C ) = n (A) + n ( B ∪ C ) – n [ A ∩ ( B ∪ C ) ] ...............[ by (2) ]
Putting, n ( B ∪ C ) = n ( B ) + n ( C ) – n ( B ∩ C ) ...............[ by (2) ] in above equation
∴ n ( A ∪ B ∪ C ) = n (A) + n ( B ) + n ( C ) – n ( B ∩ C ) – n [ A ∩ ( B ∪ C ) ] ...........[ by (2) ]
Since A ∩ ( B ∪ C ) = ( A ∩ B ) ∪ ( A ∩ C ), we get
n [ A ∩ ( B ∪ C ) ] = n ( A ∩ B ) + n ( A ∩ C ) – n [ ( A ∩ B ) ∩ (A ∩ C)]
n [ A ∩ ( B ∪ C ) ] = n ( A ∩ B ) + n ( A ∩ C ) – n (A ∩ B ∩ C)
Therefore
n ( A ∪ B ∪ C ) = n (A) + n ( B ) + n ( C ) – n ( A ∩ B ) – n ( B ∩ C) – n ( A ∩ C ) + n ( A ∩ B ∩ C ) This proves (3).
Example :
(i) If X and Y are two sets such that X ∪ Y has 50 elements, X has 28 elements and Y has 32 elements, how many elements does X ∩ Y have ?
Solution : Given that
n ( X ∪ Y ) = 50, n ( X ) = 28, n ( Y ) = 32, find n (X ∩ Y) = ?
By using the formula - n ( X ∪ Y )= n ( X ) + n ( Y ) – n ( X ∩ Y ),
we find that
n ( X ∩ Y )= n ( X ) + n ( Y ) – n ( X ∪ Y ) = 28 + 32 – 50 = 10
Alternatively, suppose n ( X ∩ Y ) = k, then
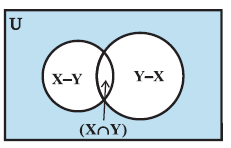
n ( X – Y ) = 28 – k , n ( Y – X ) = 32 – k (by Venn diagram in Fig )
This gives 50 = n ( X ∪ Y ) = n (X – Y) + n (X ∩ Y) + n ( Y – X)
50 = ( 28 – k ) + k + (32 – k )
Hence k = 10.
(ii) In a school there are 20 teachers who teach mathematics or physics. Of these, 12 teach mathematics and 4 teach both physics and mathematics. How many teach physics ?
Solution : Let M denote the set of teachers who teach mathematics and P denote the set of teachers who teach physics.
In the statement of the problem, the word ‘or’ gives us a clue of union and the word ‘and’ gives us a clue of
intersection. We, therefore, have
n ( M ∪ P ) = 20 , n ( M ) = 12 and n ( M ∩ P ) = 4
We wish to determine n ( P ).
Using the result
n ( M ∪ P ) = n ( M ) + n ( P ) – n ( M ∩ P ),
we obtain
20 = 12 + n ( P ) – 4
Thus n ( P ) = 12
Hence 12 teachers teach physics.
(iii) In a class of 35 students, 24 like to play cricket and 16 like to play football. Also, each student likes to play at least one of the two games. How many students like to play both cricket and football ?
Solution :
Let X be the set of students who like to play cricket and Y be the set of students who like to play football.
Then X ∪ Y is the set of students who like to play at least one game, and X Ç Y is the set of students who like to play both games.
Given n ( X) = 24, n ( Y ) = 16, n ( X ∪ Y ) = 35, n (X ∩ Y) = ?
Using the formula n ( X ∪ Y ) = n ( X ) + n ( Y ) – n ( X ∩ Y ), we get
35 = 24 + 16 – n (X ∩ Y)
Thus, n (X ∩ Y) = 5
i.e., 5 students like to play both games.
(iv) In a survey of 400 students in a school, 100 were listed as taking apple juice, 150 as taking orange juice and 75 were listed as taking both apple as well as orange juice. Find how many students were taking neither apple juice nor orange juice.
Solution : Let U denote the set of surveyed students and A denote the set of students taking apple juice and B denote the set of students taking orange juice. Then
n (U) = 400, n (A) = 100, n (B) = 150 and n (A ∩ B) = 75.
Now n (A' ∩ B') = n (A ∪ B)'
= n (U) – n (A ∪ B)
= n (U) – n (A) – n (B) + n (A ∩ B)
= 400 – 100 – 150 + 75 = 225
Hence 225 students were taking neither apple juice nor orange juice.
(v) There are 200 individuals with a skin disorder, 120 had been exposed to the chemical C1, 50 to chemical C2, and 30 to both the chemicals C1 and C2. Find the number of individuals exposed to
(i) Chemical C1 but not chemical C2 (ii) Chemical C2 but not chemical C1 (iii) Chemical C1 or chemical C2
Solution : Let U denote the universal set consisting of individuals suffering from the skin disorder, A denote the set of individuals exposed to the chemical C1 and B denote the set of individuals exposed to the chemical C2.
Here n ( U) = 200, n ( A ) = 120, n ( B ) = 50 and n ( A ∩ B ) = 30
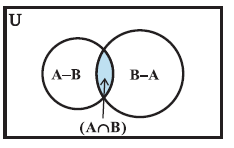
(i) From the Venn diagram given in Fig, we have
A = ( A – B ) ∪ ( A ∩ B ).
n (A) = n( A – B ) + n( A ∩ B ) (Since A – B) and A ∩ B are disjoint.)
or n ( A – B ) = n ( A ) – n ( A ∩ B ) = 120 –30 = 90
Hence, the number of individuals exposed to chemical C1 but not to chemical C2 is 90.
(ii) From the Fig we have
B = ( B – A) ∪ ( A ∩ B).
and so, n (B) = n (B – A) + n ( A ∩ B) (Since B – A and A ∩ B are disjoint.)
or n ( B – A ) = n ( B ) – n ( A ∩ B ) = 50 – 30 = 20
Thus, the number of individuals exposed to chemical C2 and not to chemical C1 is 20.
(iii) The number of individuals exposed either to chemical C1 or to chemical C2, i.e.,
n ( A ∪ B ) = n ( A ) + n ( B ) – n ( A ∩ B )
= 120 + 50 – 30 = 140.
Solution
| NCERT Class 11 Mathematics-Chapter 1- Sets- Exercise Solution |
Q1- Write the solution set of the equation x2 + x – 2 = 0 in roster form.
Solution: The given equation can be written as (x – 1) (x + 2) = 0formula(x+a)(x-b)=x2+(a+b)x-ab, i. e., x = 1, – 2
Therefore, the solution set of the given equation can be written in roster form as {1, – 2}.
Q2 Write the set {x : x is a positive integer and x2 < 40} in the roster form.
Solution : The required numbers are 1, 2, 3, 4, 5, 6. So, the given set in the roster form is {1, 2, 3, 4, 5, 6}.
Q3 Write the set A = {1, 4, 9, 16, 25, . . . }in set-builder form.
Solution: We may write the set A as
A = {x : x is the square of a natural number}
Alternatively, we can write
A = {x : x = n2, where n ∈ N}
Q4 Write the set \(\left \{\frac{1}{2},\frac{2}{3},\frac{3}{4},\frac{4}{5},\frac{5}{6},\frac{6}{7} \right\}\)in the set-builder form.
Solution We see that each member in the given set has the numerator one less than the denominator. Also, the numerator begin from 1 and do not exceed 6. Hence, in the set-builder form the given set is
\(\left \{x: x=\frac{n}{n+1} \text{ where n is natural number and }1\leq n\leq 6\right\}\)
Q5 Match each of the set on the left described in the roster form with the same set on the right described in the set-builder form :
| (i) {P, R, I, N, C, A, L} | (a) { x : x is a positive integer and is a divisor of 18} |
| (ii) { 0 } | (b) { x : x is an integer and x2 – 9 = 0} |
| (iii) {1, 2, 3, 6, 9, 18} | (c) {x : x is an integer and x + 1= 1} |
| (iv) {3, –3} | (d) {x : x is a letter of the word PRINCIPAL} |
Solution:
(i) matches (d). in (d), there are 9 letters in the word PRINCIPAL and two letters P and I are repeated.
(ii) matches (c) as x + 1 = 1 implies x = 0.
(iii) matches (a). as 1, 2 ,3, 6, 9, 18 are all divisors of 18
(iv) matches (b). as x2 – 9 = 0 implies x = 3, –3
Q1. Which of the following are sets ? Justify your answer.
(i) The collection of all the months of a year beginning with the letter J.
Answer: (i) The collection of all months of a year beginning with the letter J is a well-defined collection of objects because one can definitely identify a month that belongs to this collection. Hence, this collection is a set.
(ii) The collection of ten most talented writers of India.
Answer : (ii) The collection of ten most talented writers of India is not a well-defined collection because the criteria for determining a writer’s talent may vary from person to person. Hence, this collection is not a set.
(iii) A team of eleven best-cricket batsmen of the world.
Answer :(iii) A team of eleven best cricket batsmen of the world is not a well-defined collection because the criteria for determining a batsman’s talent may vary from person to person. Hence, this collection is not a set.
(iv) The collection of all boys in your class.
Answer: (iv) The collection of all boys in your class is a well-defined collection because you can definitely identify a boy who belongs to this collection. Hence, this collection is a set.
(v) The collection of all natural numbers less than 100.
Answer : (v) The collection of all natural numbers less than 100 is a well-defined collection because one can definitely identify a number that belongs to this collection. Hence, this collection is a set.
(vi) A collection of novels written by the writer Munshi Prem Chand
(vi) A collection of novels written by the writer Munshi Prem Chand is a well-defined collection because one can definitely identify a book that belongs to this collection. Hence, this collection is a set.
(vii) The collection of all even integers.
Answer : (vii) The collection of all even integers is a well-defined collection because one can definitely identify an even integer that belongs to this collection. Hence, this collection is a set.
(viii) The collection of questions in this Chapter.
Answer :(viii) The collection of questions in this chapter is a well-defined collection because one can definitely identify a question that belongs to this chapter. Hence, this collection is a set.
(ix) A collection of most dangerous animals of the world.
Answer : (ix) The collection of most dangerous animals of the world is not a well-defined collection because the criteria for determining the dangerousness of an animal can vary from person to person. Hence, this collection is not a set.
Q2-Let A = {1, 2, 3, 4, 5, 6}. Insert the appropriate symbol ∈ or ∉ in the blank spaces:
(i) 5. . .A (ii) 8 . . . A (iii) 0. . .A (iv) 4. . . A (v) 2. . .A (vi) 10. . .A
(i) 5 ∈ A (ii) 8 ∉ A (iii) 0 ∉ A (iv) 4 ∈ A (v) 2 ∈ A (vi) 10 ∉ A
Q3-Write the following sets in roster form.
(i) A = \(\left\{\text{x : x is an integer and -3<x<7}\right\}\)
Answer: (i) A = {x: x is an integer and –3 < x < 7} The elements of this set are –2, –1, 0, 1, 2, 3, 4, 5, and 6 only. Therefore, the given set can be written in roster form as A = {–2, –1, 0, 1, 2, 3, 4, 5, 6}
(ii) B = {x : x is a natural number less than 6}
Answer : (ii) B = {x: x is a natural number less than 6} The elements of this set are 1, 2, 3, 4, and 5 only. Therefore, the given set can be written in roster form as B = {1, 2, 3, 4, 5}
(iii) C = {x : x is a two-digit natural number such that the sum of its digits is 8}
Answer : (iii) C = {x: x is a two-digit natural number such that the sum of its digits is 8} The elements of this set are 17, 26, 35, 44, 53, 62, 71, and 80 only. Therefore, this set can be written in roster form as C = {17, 26, 35, 44, 53, 62, 71, 80}
(iv) D = {x : x is a prime number which is divisor of 60}
Answer : (iv) D = {x: x is a prime number which is a divisor of 60} 60 = 2 × 2 × 3 × 5 The elements of this set are 2, 3, and 5 only. Therefore, this set can be written in roster form as D = {2, 3, 5}.
(v) E = The set of all letters in the word TRIGONOMETRY
Answer : (v) E = The set of all letters in the word TRIGONOMETRY There are 12 letters in the word TRIGONOMETRY, out of which letters T, R, and O are repeated. Therefore, this set can be written in roster form as E = {T, R, I, G, O, N, M, E, Y}
(vi) F = The set of all letters in the word BETTER
Answer : (vi) F = The set of all letters in the word BETTER There are 6 letters in the word BETTER, out of which letters E and T are repeated. Therefore, this set can be written in roster form as F = {B, E, T, R}
Q4-Write the following sets in the set-builder form :
(i) (3, 6, 9, 12} (ii) {2,4,8,16,32} (iii) {5, 25, 125, 625} (iv) {2, 4, 6, . . .} (v) {1,4,9, . . .,100}
(i) {3, 6, 9, 12} = {x: x = 3n, n∈ N and 1 ≤ n ≤ 4} (ii) {2, 4, 8, 16, 32} It can be seen that 2 = 21, 4 = 22, 8 = 23, 16 = 24, and 32 = 25. ∴ {2, 4, 8, 16, 32} = {x: x = 2n, n∈ N and 1 ≤ n ≤ 5} (iii) {5, 25, 125, 625} It can be seen that 5 = 51, 25 = 52, 125 = 53, and 625 = 54. ∴ {5, 25, 125, 625} = {x: x = 5n, n ∈ N and 1 ≤ n ≤ 4} (iv) {2, 4, 6 …} It is a set of all even natural numbers. ∴ {2, 4, 6 …} = {x: x is an even natural number} (v) {1, 4, 9 … 100} It can be seen that 1 = 12, 4 = 22, 9 = 33 …100 = 102. ∴ {1, 4, 9… 100} = {x: x = n2, n ∈ N and 1 ≤ n ≤ 10}
Q5-List all the elements of the following sets :
(i) A = {x : x is an odd natural number}
Answer : (i) A = {x: x is an odd natural number} = {1, 3, 5, 7, 9 …}
(ii) B = {x : x is an integer, \(\frac{-1}{2} < x <\frac{9}{2}\)}
Answer :(ii) B = {x : x is an integer, \(\frac{-1}{2} < x <\frac{9}{2}\)} It can seen that \(\frac{-1}{2} =-0.5 \text{ and } \frac{9}{2} =4.5\) Therefore B = {0,1,2, 3,4}
(iii) C = {x : x is an integer, x2 ≤ 4}
Answer: (iii) It can be seen that (–1)2 = 1 ≤ 4; (–2)2 = 4 ≤ 4; (–3)2 = 9 > 4; 02 = 0 ≤ 4; 12 = 1 ≤ 4; 22 = 4 ≤ 4; 32 = 9 > 4 Therefore C = {–2, –1, 0, 1, 2}
(iv) D = {x : x is a letter in the word “LOYAL”}
Answer: (iv) D = {L, O, Y, A}
(v) E = {x : x is a month of a year not having 31 days}
Answer: E = {February, April, June, September, November}
(vi) F = {x : x is a consonant in the English alphabet which precedes k }.
Answer: F= {b, c, d, f, g, h, j}
Q6-Match each of the set on the left in the roster form with the same set on the right described in set-builder form:
| (I) {1, 2, 3, 6} | (A) {X: X IS A PRIME NUMBER AND A DIVISOR OF 6} |
| (II) {2, 3} | (B) {X: X IS AN ODD NATURAL NUMBER LESS THAN 10} |
| (III) {M, A,T, H, E, I,C, S} | (C) {X: X IS NATURAL NUMBER AND DIVISOR OF 6} |
| (IV) {1, 3, 5, 7, 9} | (D) {X: X IS A LETTER OF THE WORD MATHEMATICS} |
Answer 6: (i) All the elements of this set are natural numbers as well as the divisors of 6. Therefore, (i) matches with (c). (ii)It can be seen that 2 and 3 are prime numbers. They are also the divisors of 6. Therefore, (ii) matches with (a). (iii) All the elements of this set are letters of the word MATHEMATICS. Therefore, (iii) matches with (d). (iv) All the elements of this set are odd natural numbers less than 10. Therefore, (iv) matches with (b).
Q-Which of the following pairs of sets are equal? Justify your answer.
(i) X, the set of letters in “ALLOY” and B, the set of letters in “LOYAL”.
Answer :We have, X = {A, L, L, O, Y}, B = {L, O, Y, A, L}. Then X and B are equal sets as repetition of elements in a set do not change a set.
Thus, X = {A, L, O, Y} = B
(ii) A = {n : n ∈ Z and n2 ≤ 4} and B = {x : x ∈ R and x2 – 3x + 2 = 0}.
Answer : A = {–2, –1, 0, 1, 2}, B = {1, 2}. Since 0 ∈ A and 0 ∉ B, A and B are not equal sets.
Q1-Which of the following are examples of the null set.
(i) Set of odd natural numbers divisible by 2.
Answer : A set of odd natural numbers divisible by 2 is a null set because no odd number is divisible by 2.
(ii) Set of even prime numbers.
Answer : A set of even prime numbers is not a null set because 2 is an even prime number.
(iii) {x:x is a natural numbers, x < 5 and x > 7 }
Answer : {x: x is a natural number, x < 5 and x > 7} is a null set because a number cannot be simultaneously less than 5 and greater than 7.
(iv) {y:y is a point common to any two parallel lines}
Answer : {y: y is a point common to any two parallel lines} is a null set because parallel lines do not intersect. Hence, they have no common point.
Q2-Which of the following sets are finite or infinite
(i) The set of months of a year.
Answer : The set of months of a year is a finite set because it has 12 elements.
(ii) {1, 2, 3 ...}
Answer : {1, 2, 3 …} is an infinite set as it has infinite number of natural numbers.
(iii) {1, 2, 3 ... 99, 100}
Answer : {1, 2, 3 …99, 100} is a finite set because the numbers from 1 to 100 are finite in number.
(iv) The set of positive integers greater than 100
Answer :The set of positive integers greater than 100 is an infinite set because positive integers greater than 100 are infinite in number.
(v) The set of prime numbers less than 99.
Answer : The set of prime numbers less than 99 is a finite set because prime numbers less than 99 are finite in number.
Q3-State whether each of the following set is finite or infinite:
(i) The set of lines which are parallel to the x-axis
Answer: The set of lines which are parallel to the x-axis is an infinite set because, lines parallel to the x-axis are infinite in number.
(ii) The set of letters in the English alphabet
Answer: The set of letters in the English alphabet is a finite set because it has 26 elements.
(iii) The set of numbers which are multiple of 5
Answer:The set of numbers which are multiple of 5 is an infinite set because multiples of 5 are infinite in number.
(iv) The set of animals living on the earth
Answer: The set of animals living on the earth is a finite set because the number of animals living on the earth is finite (although it is quite a big number).
(v) The set of circles passing through the origin (0, 0)
Answer:The set of circles passing through the origin (0, 0) is an infinite set because infinite number of circles can pass through the origin.
Q4-In the following, state whether A = B or not:
(i) A = {a, b, c, d}; B = {d, c, b, a}
Answer: A = {a, b, c, d}; B = {d, c, b, a} – The order in which the elements of a set are listed is not significant.
∴ A = B
(ii) A = {4, 8, 12, 16}; B = {8, 4, 16, 18}
Answer: A = {4, 8, 12, 16}; B = {8, 4, 16, 18} -It can be seen that 12 ∈ A but 12 ∉ B.
∴ A ≠ B
(iii) A = {2, 4, 6, 8, 10}; B = {x: x is positive even integer and x ≤ 10}
Answer:A = {2, 4, 6, 8, 10} B = {x: x is a positive even integer and x ≤ 10} = {2, 4, 6, 8, 10}
∴ A = B
(iv) A = {x: x is a multiple of 10}; B = {10, 15, 20, 25, 30 ...}
Answer: A = {x: x is a multiple of 10} B = {10, 15, 20, 25, 30 …}- It can be seen that 15 ∈ B but 15 ∉ A.
∴ A ≠ B
Q5-Are the following pair of sets equal? Give reasons.
(i) A = {2, 3}; B = {x: x is solution of x2 + 5x + 6 = 0}
Answer: A = {2, 3}; B = {x: x is a solution of x2 + 5x + 6 = 0}
The equation x2 + 5x + 6 = 0 can be solved as: x(x + 3) + 2(x + 3) = 0
(x + 2)(x + 3) = 0 ; x = –2 or x = –3
∴ A = {2, 3}; B = {–2, –3}
∴ A ≠ B
(ii) A = {x: x is a letter in the word FOLLOW}; B = {y: y is a letter in the word WOLF}
Answer: A = {x: x is a letter in the word FOLLOW} = {F, O, L, W}
B = {y: y is a letter in the word WOLF} = {W, O, L, F}
The order in which the elements of a set are listed is not significant.
∴ A = B
Q6- From the sets given below, select equal sets:
A = {2, 4, 8, 12}, B = {1, 2, 3, 4}, C = {4, 8, 12, 14}, D = {3, 1, 4, 2}, E = {–1, 1}, F = {0, a}, G = {1, –1}, H = {0, 1}
Answer: It can be seen that Consider set A, from set A Consider set B, from set B Consider set C, from set C Consider set D, from set D
8 ∈ A, 8 ∉ B, 8 ∉ D, 8 ∉ E, 8 ∉ F, 8 ∉ G, 8 ∉ H
⇒ A ≠ B, A ≠ D, A ≠ E, A ≠ F, A ≠ G, A ≠ H
Also, 2 ∈ A, 2 ∉ C
∴ A ≠ C
3 ∈ B, 3 ∉ C, 3 ∉ E, 3 ∉ F, 3 ∉ G, 3 ∉ H
∴ B ≠ C, B ≠ E, B ≠ F, B ≠ G, B ≠ H
12 ∈ C, 12 ∉ D, 12 ∉ E, 12 ∉ F, 12 ∉ G, 12 ∉ H
∴ C ≠ D, C ≠ E, C ≠ F, C ≠ G, C ≠ H
4 ∈ D, 4 ∉ E, 4 ∉ F, 4 ∉ G, 4 ∉ H
∴ D ≠ E, D ≠ F, D ≠ G, D ≠ H
Similarly, E ≠ F, E ≠ H, F ≠ G, F ≠ H, G ≠ H
The order in which the elements of a set are listed is not significant.
∴ B = D and E = G
Hence, among the given sets, B = D and E = G.
Q1-Make correct statements by filling in the symbols ⊂ or ⊄ in the blank spaces:
(i) {2, 3, 4} … {1, 2, 3, 4, 5}
Answer : {2, 3, 4} ⊂ {1, 2, 3, 4, 5}
(ii) {a, b, c} … {b, c, d}
Answer : {a, b, c} ⊄ {b, c, d}
(iii) {x: x is a student of Class XI of your school} … {x: x student of your school}
Answer : {x: x is a student of class XI of your school}⊂ {x: x is student of your school}
(iv) {x: x is a circle in the plane} … {x: x is a circle in the same plane with radius 1 unit}
Answer : {x: x is a circle in the plane} ⊄ {x: x is a circle in the same plane with radius 1 unit}
(v) {x: x is a triangle in a plane}…{x: x is a rectangle in the plane}
Answer : {x: x is a triangle in a plane} ⊄ {x: x is a rectangle in the plane}
(vi) {x: x is an equilateral triangle in a plane}… {x: x is a triangle in the same plane}
Answer : {x: x is an equilateral triangle in a plane}⊂ {x: x in a triangle in the same plane}
(vii) {x: x is an even natural number} … {x: x is an integer}
Answer : {x: x is an even natural number} ⊂ {x: x is an integer}
Q2-Examine whether the following statements are true or false.
(i) {a, b} ⊄ {b, c, a}
Answer : False. Each element of {a, b} is also an element of {b, c, a}.
(ii) {a, e} ⊂ {x: x is a vowel in the English alphabet}
Answer : True. a, e are two vowels of the English alphabet.
(iii) {1, 2, 3} ⊂{1, 3, 5}
Answer : False. 2∈{1, 2, 3}; however, 2∉{1, 3, 5}
(iv) {a} ⊂ {a. b, c}
Answer : True. Each element of {a} is also an element of {a, b, c}.
(v) {a} ∈ (a, b, c)
Answer : False. The elements of {a, b, c} are a, b, c. Therefore, {a}⊂{a, b, c}
(vi) {x: x is an even natural number less than 6} ⊂ {x: x is a natural number which divides 36}
Answer : True. {x:x is an even natural number less than 6} = {2, 4} , {x:x is a natural number which divides 36}= {1, 2, 3, 4, 6, 9, 12, 18, 36}
Q3- Let A= {1, 2, {3, 4,}, 5}. Which of the following statements are incorrect and why?
(i) {3, 4}⊂ A
Answer : The statement {3, 4} ⊂ A is incorrect because 3 ∈ {3, 4}; however, 3∉A.
(ii) {3, 4} ∈ A
Answer : The statement {3, 4} ∈A is correct because {3, 4} is an element of A.
(iii) {{3, 4}}⊂ A
Answer : The statement {{3, 4}} ⊂ A is correct because {3, 4} ∈ {{3, 4}} and {3, 4} ∈ A.
(iv) 1∈ A
Answer : The statement 1∈A is correct because 1 is an element of A.
(v) 1⊂ A
Answer : The statement 1⊂ A is incorrect because an element of a set can never be a subset of itself.
(vi) {1, 2, 5} ⊂ A
Answer : The statement {1, 2, 5} ⊂ A is correct because each element of {1, 2, 5} is also an element of A.
(vii) {1, 2, 5} ∈ A
Answer : The statement {1, 2, 5} ∈ A is incorrect because {1, 2, 5} is not an element of A.
(viii) {1, 2, 3} ⊂ A
Answer : The statement {1, 2, 3} ⊂ A is incorrect because 3 ∈ {1, 2, 3}; however, 3 ∉ A.
(ix) Φ ∈ A
Answer : The statement Φ ∈ A is incorrect because Φ is not an element of A.
(x) Φ ⊂ A
Answer : The statement Φ ⊂ A is correct because Φ is a subset of every set.
(xi) {Φ} ⊂ A
Answer : The statement {Φ} ⊂ A is incorrect because Φ∈ {Φ}; however, Φ ∈ A.
Q4- Write down all the subsets of the following sets.
(i) {a}
Answer : The subsets of {a} are Φ and {a}.
(ii) {a, b}
Answer : The subsets of {a, b} are Φ, {a}, {b}, and {a, b}.
(iii) {1, 2, 3}
Answer : The subsets of {1, 2, 3} are Φ, {1}, {2}, {3}, {1, 2}, {2, 3}, {1, 3} and {1, 2, 3}
(iv) Φ
Answer : The only subset of Φ is Φ.
Q5-How many elements has P(A), if A = Φ?
Answer : We know that if A is a set with m elements i.e., n(A) = m, then n[P(A)] = 2m.
If A = Φ, then n(A) = 0.
∴ n[P(A)] = 20 = 1
Hence, P(A) has one element.
Q6- Write the following as intervals.
(i) {x: x ∈ R, –4 < x ≤ 6}
Answer : {x: x ∈ R, –4 < x ≤ 6} = (–4, 6]
(ii) {x: x ∈ R, –12 < x < –10}
Answer : {x: x ∈ R, –12 < x < –10} = (–12, –10)
(iii) {x: x ∈ R, 0 ≤ x < 7}
Answer : {x: x ∈ R, 0 ≤ x < 7} = [0, 7)
(iv) {x: x ∈ R, 3 ≤ x ≤ 4}
Answer : {x: x ∈ R, 3 ≤ x ≤ 4} = [3, 4]
Q7- Write the following intervals in set-builder form:
(i) (–3, 0)
Answer : (–3, 0) = {x: x ∈ R, –3 < x < 0}
(ii) [6, 12]
Answer : [6, 12] = {x: x ∈ R, 6 ≤ x ≤ 12}
(iii) (6, 12]
Answer : (6, 12] ={x: x ∈ R, 6 < x ≤ 12}
(iv) [–23, 5)
Answer : [–23, 5) = {x: x ∈ R, –23 ≤ x < 5}
Q8-What universal set (s) would you propose for each of the following?
(i) The set of right triangles
(ii) The set of isosceles triangles
Answer : (i) For the set of right triangles, the universal set can be the set of triangles or the set of polygons.
(ii) For the set of isosceles triangles, the universal set can be the set of triangles or the set of polygons or the set of two-dimensional figures.
Q9-Given the sets A = {1, 3, 5}, B = {2, 4, 6} and C = {0, 2, 4, 6, 8}, which of the following may be considered as universals set (s) for all the three sets A, B and C Answer : It can be seen that A ⊂ {0, 1, 2, 3, 4, 5, 6} B ⊂ {0, 1, 2, 3, 4, 5, 6}
(i) {0, 1, 2, 3, 4, 5, 6}
However, C ⊄ {0, 1, 2, 3, 4, 5, 6}
Therefore, the set {0, 1, 2, 3, 4, 5, 6} cannot be the universal set for the sets A, B, and C.
(ii) Φ
Answer : A ⊄ Φ, B ⊄ Φ, C ⊄ Φ
Therefore, Φ cannot be the universal set for the sets A, B, and C.
(iii) {0, 1, 2, 3, 4, 5, 6, 7, 8, 9, 10}
Answer : A ⊂ {0, 1, 2, 3, 4, 5, 6, 7, 8, 9, 10}, B ⊂ {0, 1, 2, 3, 4, 5, 6, 7, 8, 9, 10}, C ⊂ {0, 1, 2, 3, 4, 5, 6, 7, 8, 9, 10}
Therefore, the set {0, 1, 2, 3, 4, 5, 6, 7, 8, 9, 10} is the universal set for the sets A, B, and C.
(iv) {1, 2, 3, 4, 5, 6, 7, 8}
Answer : A ⊂ {1, 2, 3, 4, 5, 6, 7, 8}, B ⊂ {1, 2, 3, 4, 5, 6, 7, 8}, However, C ⊄ {1, 2, 3, 4, 5, 6, 7, 8}
Therefore, the set {1, 2, 3, 4, 5, 6, 7, 8} cannot be the universal set for the sets A, B, and C.
Q-1: Find the union of each of the following pairs of sets.
(i) X = {1, 3, 5}; Y = {1, 2, 3}
Answer : X ∪ Y= {1, 2, 3, 5}
(ii) A = {a, e, i, o, u}; B = {a, b, c}
Answer : A ∪ B = {a, b, c, e, i, o, u}
(iii) A = {x: x is a natural number and multiple of 3}, B = {x: x is a natural number less than 6}
Answer : A = {x: x is a natural number and multiple of 3} = {3, 6, 9 …}, B = {x: x is a natural number less than 6} = {1, 2, 3, 4, 5, 6} A ∪ B = {1, 2, 4, 5, 3, 6, 9, 12 …} ∴ A ∪ B = {x: x = 1, 2, 4, 5 and a multiple of 3}
(iv) A = {x: x is a natural number and 1 < x ≤ 6}, B = {x: x is a natural number and 6 < x < 10}
Answer : A = {x: x is a natural number and 1 < x ≤ 6} = {2, 3, 4, 5, 6}
B = {x: x is a natural number and 6 < x < 10} = {7, 8, 9}
A ∪ B = {2, 3, 4, 5, 6, 7, 8, 9}
∴ A∪ B = {x: x ∈ N and 1 < x < 10}
(v) A = {1, 2, 3}; B = Φ
Answer : A = {1, 2, 3}, B = Φ ∴ A ∪ B = {1, 2, 3}
Q-2: Let A = {a, b}, B = {a, b, c}. Is A ⊂ B? What is A ∪ B?
Answer : Here, A = {a, b} and B = {a, b, c}
Yes, A ⊂ B.
A ∪ B = {a, b, c} = B
Q- 3: If A and B are two sets such that A ⊂ B, then what is A ∪ B?
Answer : If A and B are two sets such that A ⊂ B, then A ∪ B = B.
Q- 4: If A = {1, 2, 3, 4}, B = {3, 4, 5, 6}, C = {5, 6, 7, 8} and D = {7, 8, 9, 10}; find
(i) A ∪ B
Answer : A ∪ B = {1, 2, 3, 4, 5, 6}
(ii) A ∪ C
Answer : A ∪ C = {1, 2, 3, 4, 5, 6, 7, 8}
(iii) B ∪ C
Answer : B ∪ C = {3, 4, 5, 6, 7, 8}
(iv) B ∪ D
Answer : B ∪ D = {3, 4, 5, 6, 7, 8, 9, 10}
(v) A ∪ B ∪ C
Answer : A ∪ B ∪ C = {1, 2, 3, 4, 5, 6, 7, 8}
(vi) A ∪ B ∪ D
Answer : A ∪ B ∪ D = {1, 2, 3, 4, 5, 6, 7, 8, 9, 10}
(vii) B ∪ C ∪ D
Answer : B ∪ C ∪ D = {3, 4, 5, 6, 7, 8, 9, 10}
Q- 5: Find the intersection of each pair of sets.
(i) X = {1, 3, 5} Y = {1, 2, 3}
Answer : X ∩ Y = {1, 3}
(ii) A = {a, e, i, o, u} B = {a, b, c}
Answer : A ∩ B = {a}
(iii) A = {x: x is a natural number and multiple of 3}, B = {x: x is a natural number less than 6}
Answer : A = {x: x is a natural number and multiple of 3} = (3, 6, 9 …}
B = {x: x is a natural number less than 6} = {1, 2, 3, 4, 5}
∴ A ∩ B = {3}
(iv) A = {x: x is a natural number and 1 < x ≤ 6}, B = {x: x is a natural number and 6 < x < 10}
Answer : A = {x: x is a natural number and 1 < x ≤ 6} = {2, 3, 4, 5, 6}
B = {x: x is a natural number and 6 < x < 10} = {7, 8, 9}
∴ A ∩ B = Φ
(v) A = {1, 2, 3}, B = Φ
Answer : A ∩ B = Φ
Q- 6: If A = {3, 5, 7, 9, 11}, B = {7, 9, 11, 13}, C = {11, 13, 15} and D = {15, 17}; find
(i) A ∩ B
Answer : A ∩ B = {7, 9, 11}
(ii) B ∩ C
Answer : B ∩ C = {11, 13}
(iii) A ∩ C ∩ D
Answer : A ∩ C ∩ D = { A ∩ C} ∩ D = {11} ∩ {15, 17} = Φ
(iv) A ∩ C
Answer : A ∩ C = {11}
(v) B ∩ D
Answer : B ∩ D = Φ
(vi) A ∩ (B ∪ C)
Answer : A ∩ (B ∪ C) = (A ∩ B) ∪ (A ∩ C)
= {7, 9, 11} {11} = {7, 9, 11}
(vii) A ∩ D
Answer : A ∩ D = Φ
(viii) A ∩ (B ∪ D)
Answer : A ∩ (B ∪ D) = (A ∩ B) ∪ (A ∩ D)
= {7, 9, 11} ∪ Φ = {7, 9, 11}
(ix) (A ∩ B) ∩ (B C)
Answer : (A ∩ B) ∩ (B ∪ C) = {7, 9, 11} ∩ {7, 9, 11, 13, 15} = {7, 9, 11}
(x) (A D) ∩ (B C)
Answer : (A ∪ D) ∩ (B ∪ C) = {3, 5, 7, 9, 11, 15, 17) ∩ {7, 9, 11, 13, 15} = {7, 9, 11, 15}
Q-7: If A = {x: x is a natural number}, B ={x: x is an even natural number} C = {x: x is an odd natural number} and D = {x: x is a prime number}, find
(i) A ∩ B
Answer : A ∩B = {x: x is a even natural number} = B
(ii) A ∩ C
Answer : A ∩ C = {x: x is an odd natural number} = C
(iii) A ∩ D
Answer : A ∩ D = {x: x is a prime number} = D
(iv) B ∩ C
Answer : B ∩ C = Φ
(v) B ∩ D
Answer : B ∩ D = {2}
(vi) C ∩ D
Answer : C ∩ D = {x: x is odd prime number}
Q- 8: Which of the following pairs of sets are disjoint
(i) {1, 2, 3, 4} and {x: x is a natural number and 4 ≤ x ≤ 6}
Answer : {1, 2, 3, 4}
{x: x is a natural number and 4 ≤ x ≤ 6} = {4, 5, 6}
Now, {1, 2, 3, 4} ∩ {4, 5, 6} = {4}
Therefore, this pair of sets is not disjoint
(ii) {a, e, i, o, u} and {c, d, e, f}
Answer : {a, e, i, o, u} ∩ (c, d, e, f} = {e}
Therefore, {a, e, i, o, u} and (c, d, e, f} are not disjoint.
(iii) {x: x is an even integer} and {x: x is an odd integer}
Answer : {x: x is an even integer} ∩ {x: x is an odd integer} = Φ
Therefore, this pair of sets is disjoint.
Q- 9: If A = {3, 6, 9, 12, 15, 18, 21}, B = {4, 8, 12, 16, 20}, C = {2, 4, 6, 8, 10, 12, 14, 16}, D = {5, 10, 15, 20}; find
(i) A – B
Answer : A – B = {3, 6, 9, 15, 18, 21}
(ii) A – C
Answer : A – C = {3, 9, 15, 18, 21}
(iii) A – D
Answer : A – D = {3, 6, 9, 12, 18, 21}
(iv) B – A
Answer : B – A = {4, 8, 16, 20}
(v) C – A
Answer : C – A = {2, 4, 8, 10, 14, 16}
(vi) D – A
Answer : D – A = {5, 10, 20}
(vii) B – C
Answer : B – C = {20}
(viii) B – D
Answer : B – D = {4, 8, 12, 16}
(ix) C – B
Answer : C – B = {2, 6, 10, 14}
(x) D – B
Answer : D – B = {5, 10, 15}
(xi) C – D
Answer : C – D = {2, 4, 6, 8, 12, 14, 16}
(xii) D – C
Answer : D – C = {5, 15, 20}
Q-10: If X = {a, b, c, d} and Y = {f, b, d, g}, find
(i) X – Y, (ii) Y – X, (iii) X ∩ Y
Answer : (i) X – Y = {a, c}
(ii) Y – X = {f, g}
(iii) X ∩ Y = {b, d}
Q-11: If R is the set of real numbers and Q is the set of rational numbers, then what is R – Q?
Answer : R: set of real numbers, Q: set of rational numbers
Therefore, R – Q is a set of irrational numbers.
Q-12: State whether each of the following statement is true or false. Justify your answer.
(i) {2, 3, 4, 5} and {3, 6} are disjoint sets.
Answer : False -As 3 ∈ {2, 3, 4, 5}, 3 ∈ {3, 6}
⇒ {2, 3, 4, 5} ∩ {3, 6} = {3}
(ii) {a, e, i, o, u } and {a, b, c, d} are disjoint sets.
Answer : False -As a ∈ {a, e, i, o, u}, a ∈ {a, b, c, d}
⇒ {a, e, i, o, u } ∩ {a, b, c, d} = {a}
(iii) {2, 6, 10, 14} and {3, 7, 11, 15} are disjoint sets.
Answer : True -As {2, 6, 10, 14} ∩ {3, 7, 11, 15} = Φ
(iv) {2, 6, 10} and {3, 7, 11} are disjoint sets.
Answer : True – As {2, 6, 10} ∩ {3, 7, 11} = Φ
Q-1: Let U ={1, 2, 3; 4, 5, 6, 7, 8, 9}, A = {1, 2, 3, 4}, B = {2, 4, 6, 8} and C = {3, 4, 5, 6}. Find
(i) A'
Answer : A’= {5, 6, 7, 8, 9}
(ii) B'
Answer : B’= {1, 3, 5, 7, 9}
(iii) (A ∪ C)'
Answer : A ∪ C= {1, 2, 3, 4, 5, 6} ∴ (A ∪ C)’= {7, 8, 9}
(iv) (A ∪ B)'
Answer : A ∪ B= { 1, 2, 3, 4, 6, 8 } ∴ (A ∪ B)’= {5, 7, 9}
(v) (A')'
Answer : (A’)’= A = { 1, 2, 3, 4,}
(vi) (B – C)'
Answer : B – C = { 2, 8 } (B – C)’ = { 1, 3, 4, 5, 6, 7, 9, }
Q- 2: If U = {a, b, c, d, e, f, g, h}, find the complements of the following sets:
(i) A = {a, b, c}
Answer : A’ = {d, e, f, g, h}
(ii) B = {d, e, f, g}
Answer : B’ = {a, b, c, h}
(iii) C = {a, c, e, g}
Answer : C’ = { b, d, f, h}
(iv) D = {f, g, h, a}
Answer : D’ = { b, c, d, e }
Q- 3: Taking the set of natural numbers as the universal set, write down the complements of the following sets.
(i) {x: x is an even natural number}
Answer : {x: x is an even natural number}´ = {x: x is an odd natural number}
(ii) {x: x is an odd natural number}
Answer : {x: x is an odd natural number}´ = {x: x is an even natural number}
(iii) {x: x is a positive multiple of 3}
Answer : {x: x is a positive multiple of 3}´= {x: x N and x is not a multiple of 3}
(iv) {x: x is a prime number}
Answer : {x: x is a prime number}´ ={x: x is a positive composite number and x = 1}
(v) {x: x is a natural number divisible by 3 and 5}
Answer : {x: x is a natural number divisible by 3 and 5}´ = {x: x is a natural number that is not divisible by 3 or 5}
(vi) {x: x is a perfect square}
Answer : {x: x is a perfect square}´ = {x: x ∈ N and x is not a perfect square}
(vii) {x: x is perfect cube}
Answer : {x: x is a perfect cube}´ = {x: x ∈ N and x is not a perfect cube}
(viii) {x: x + 5 = 8}
Answer : {x: x + 5 = 8}´ = {x: x ∈ N and x ≠ 3}
(ix) {x: 2x + 5 = 9}
Answer : {x: 2x + 5 = 9}´ = {x: x ∈ N and x ≠ 2}
(x) {x: x ≥ 7}
Answer : {x: x ≥ 7}´ = {x: x ∈ N and x < 7}
(xi) {x: x ∈ N and 2x + 1 > 10}
Answer : {x: x ∈ N and 2x + 1 > 10}´ = {x: x ∈ N and x ≤ 9/2}
Q- 4: If U = {1, 2, 3, 4, 5,6,7,8, 9}, A = {2, 4, 6, 8} and B = {2, 3, 5, 7}. Verify that
(i) ( A ∪ B )' = A' ∩ B'
Answer : ( A ∪ B )’ = { 2, 3, 4, 5,6,7,8 }’ = {1, 9} A’ ∩ B’ = {1, 3, 5, 7, 9} ∩ {1, 4, 6, 8, 9} = {1, 9}
(ii) ( A ∩ B )' = A' ∪ B'
Answer : ( A ∩ B )’ = { 2}’ = { 1, 3, 4, 5, 6, 7, 8, 9 }’ A’ ∪ B’ = {1, 3, 5, 7, 9} ∪ {1, 4, 6, 8, 9} = { 1, 3, 4, 5, 6, 7, 8, 9 }
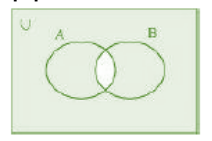
Q-5: Draw appropriate Venn diagram for each of the following.
(i) ( A ∪ B )' (ii) A' ∩ B' (iii) ( A ∩ B )' (iv) A' ∪ B'
Answer for – (i) ( A ∪ B )’ (ii) A’ ∩ B’
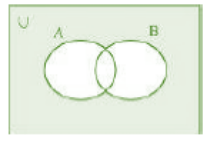
Answer for – (iii) ( A ∩ B )’ (iv) A’ ∪ B’
Q-6: Let U be the set of all triangles in a plane. If A is the set of all triangles with at least one angle different from 60°, what is A' ?
Answer : A’ is the set of all equilateral triangles
Q-7: Fill in the blanks to make each of the following a true statement.
(i) A ∪ A' = .....
Answer : A ∪ A’ = U
(ii) Φ′ ∩ A = …
Answer : Φ′ ∩ A = U ∩ A = A
∴ Φ′ ∩ A = A
(iii) A ∩ A' = .....
Answer : A ∩ A′ = Φ
(iv) U' ∩ A =.....
Answer : U′ ∩ A = Φ ∩ A = Φ
∴ U′ ∩ A = Φ
Q- 1: If X and Y are two sets such that n(X) = 17, n(Y) = 23 and n(X ∪ Y) = 38, find n(X ∩Y).
Answer : It is given that: n(X ∩ Y) = ? We know that: n(X ∪ Y) = n(X) + n(Y) – n(X ∩ Y) 38 = 17 + 23 – n(X ∩ Y) n(X ∩ Y) =40 – 38 = 2
n(X) = 17, n(Y) = 23, n(X ∪ Y) = 38
Q-2: If X and Y are two sets such that X ∪ Y has 18 elements, X has 8 elements and Y has 15 elements; how many elements does X ∩ Y have?
Answer : It is given that: n(X ∩ Y) = ? We know that: n(X ∪ Y) = n(X) + n(Y) – n(X ∩ Y) 18 = 8 + 15 – n(X ∩ Y) n(X ∩ Y) = 23 – 18 = 5
n(X) = 8, n(Y) = 15, n(X ∪ Y) = 18
Q-3: In a group of 400 people, 250 can speak Hindi and 200 can speak English. How many people can speak both Hindi and English?
Answer : Let H be the set of people who speak Hindi, and E be the set of people who speak English ∴ n(H ∪ E) = 400, n(H) = 250, n(E) = 200 n(H ∩ E) = ? We know that: n(H ∪ E) = n(H) + n(E) – n(H ∩ E) ∴ 400 = 250 + 200 – n(H ∩ E) ⇒ 400 = 450 – n(H ∩ E) ⇒ n(H ∩ E) = 450 – 400 ∴ n(H ∩ E) = 50 Thus, 50 people can speak both Hindi and English.
Q-4: If S and T are two sets such that S has 21 elements, T has 32 elements, and S ∩ T has 11 elements, how many elements does S ∪ T have?
Answer : It is given that: n(S) = 21, n(T) = 32, n(S ∩ T) = 11 We know that: n (S ∪ T) = n (S) + n (T) – n (S ∩ T) ∴ n (S ∪ T) = 21 + 32 – 11 = 42 Thus, the set (S ∪ T) has 42 elements.
Q-5: If X and Y are two sets such that X has 40 elements, X ∪Y has 60 elements and X ∩Y has 10 elements, how many elements does Y have?
Answer : It is given that: n(X) = 40, n(X ∪ Y) = 60, n(X ∩ Y) = 10 We know that: n(X ∪ Y) = n(X) + n(Y) – n(X ∩ Y) ∴ 60 = 40 + n(Y) – 10 ∴ n(Y) = 60 – (40 – 10) = 30 Thus, the set Y has 30 elements.
Q-6: In a group of 70 people, 37 like coffee, 52 like tea, and each person likes at least one of the two drinks. How many people like both coffee and tea?
Answer : Let C denote the set of people who like coffee, and T denote the set of people who like tea n(C ∪ T) = 70, n(C) = 37, n(T) = 52 We know that: n(C ∪ T) = n(C) + n(T) – n(C ∩ T) ∴ 70 = 37 + 52 – n(C ∩ T) ⇒ 70 = 89 – n(C ∩ T) ⇒ n(C ∩ T) = 89 – 70 = 19 Thus, 19 people like both coffee and tea.
Q-7: In a group of 65 people, 40 like cricket, 10 like both cricket and tennis. How many like tennis only and not cricket? How many like tennis?
Answer : Let C denote the set of people who like cricket, and T denote the set of people who like tennis ∴ n(C ∪ T) = 65, n(C) = 40, n(C ∩ T) = 10 We know that: n(C ∪ T) = n(C) + n(T) – n(C ∩ T) ∴ 65 = 40 + n(T) – 10 ⇒ 65 = 30 + n(T) ⇒ n(T) = 65 – 30 = 35 Therefore, 35 people like tennis. Now, (T – C) ∪ (T ∩ C) = T Also, (T – C) ∩ (T ∩ C) = Φ ∴ n (T) = n (T – C) + n (T ∩ C) ⇒ 35 = n (T – C) + 10 ⇒ n (T – C) = 35 – 10 = 25 Thus, 25 people like only tennis.
Q-8: In a committee, 50 people speak French, 20 speak Spanish and 10 speak both Spanish and French. How many speak at least one of these two languages?
Answer : Let F be the set of people in the committee who speak French, and S be the set of people in the committee who speak Spanish ∴ n(F) = 50, n(S) = 20, n(S ∩ F) = 10 We know that: n(S ∪ F) = n(S) + n(F) – n(S ∩ F) = 20 + 50 – 10 = 70 – 10 = 60 Thus, 60 people in the committee speak at least one of the two languages
Videos
| NCERT Class 11 Mathematics Chapter 1 Sets - videos by topics |
Click on below link to Watch
3- Roster form and set builder form
4- Numerical Roster and set builder form
5- Empty, finite and infinite set
6- Equal set
8- Singleton , Power and Universal set
10- Venn Diagram
11- Union of Set
13- Difference and complement of set
14- Venn Diagram Numerical Questions
15- Element count
16- Solution
Click on below link to download PDF
Visit Main Page : CBSE-NCERT-Class 11 -Mathematics to view online solutions, notes, Videos, Test of all chapters, & to download Books, Notes, Solutions PDF of all chapters.