Unit 1 Some Basic Concepts of Chemistry 

1.1 Importance of Chemistry 

1.2 Nature of Matter 

1.3 Properties of Matter and their Measurement 

1.4 Uncertainty in Measurement 

1.5 Laws of Chemical Combinations 

1.6 Dalton’s Atomic Theory 

1.7 Atomic and Molecular Masses 

1.8 Mole Concept and Molar Masses 

1.9 Percentage Composition 

1.10 Stoichiometry and Stoichiometric Calculations

Chemistry is the science of molecules, variety of compounds and transformations.

Chemistry has increased the comforts in the human life.

Like the two sides of a coin, on one side with many advantages due to the development of chemistry, on the other hand there is a possibility of tremendous damage to the human life and environment.

In the present circumstances some of the efforts made in chemistry have successfully resulted in solving (abating) the global problems like pollution.

Matter : Anything that has mass and occupies Space is matter. 

Matter is made up of particles.

Classification based on physical states:

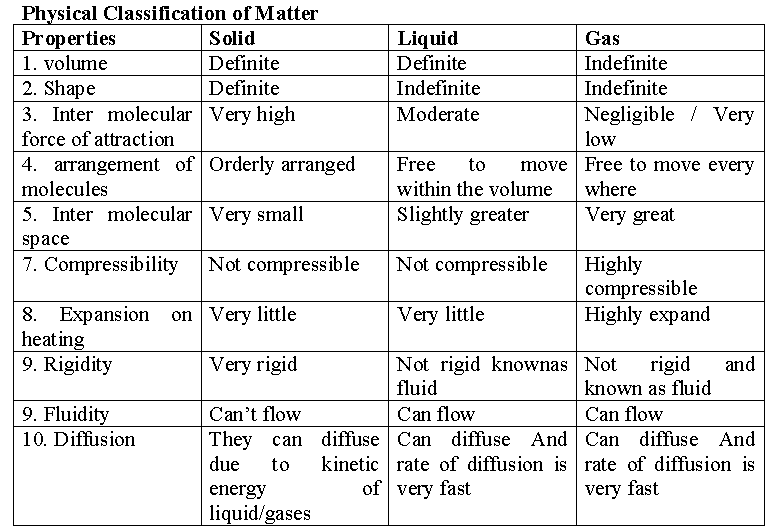
Matter can exit in three physical states : (1) solid  (2) liquid and (3) gas.

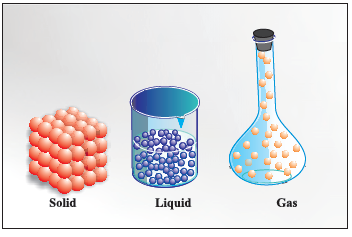
Arrangement of particles in solid, liquid and gaseous state.

(i) Solids have definite volume and definite shape.

(ii) Liquids have definite volume but do not have definite shape. They take the shape of the container in which they are placed.

(iii) Gases have neither definite volume nor definite shape. They completely occupy the space in the container in which they are placed.

These three states of matter are inter convertible by changing the conditions of temperature and pressure.

---

Classification based on chemical structure :

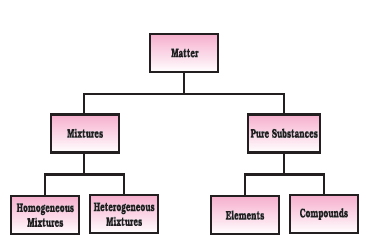
Mixture : A mixture is a material consisting of two or more kinds of matter, each retaining its own characteristic properties.

Mixture can be separated by physical methods.

Mixture can be classified in two different categories : (i) Homogeneous mixture (ii) Heterogeneous mixture

(i) Homogeneous mixture : In the homogeneous mixture the components are in same physical state.

Example : mixture of sugar and water (sugar solution), salt and water (salt solution), oxygen and nitrogen (air), zinc and copper (alloy brass).

(ii) Heterogeneous mixture : In the heterogeneous mixture the components are different in their physical state.

In the heterogeneous mixture the components do not mix with each other.

Example :  sodium chloride (NaCl) mixed with iron (Fe)

Pure substances : Constituent particles of pure substances have fixed composition.
Examples : Copper, silver, gold, water and glucose are some examples of pure substances.

Element: Element consists of only one type of atoms.

Thus, every element has its own independent property which is not the same in other elements,
Example : carbon, sodium, oxygen etc.

Compound : When two or more elements combine chemically with one another compound is formed.  When the compounds are formed, the elements present m them show new type of properties by losing their own individual properties.

For example, hydrogen (H) and oxygen (O) are gases, water (H₂O) formed by their combination is a liquid.

Here, hydrogen burns explosively in air and oxygen is a supporter of combustion; but water is used as a fire extinguisher.

Thus, hydrogen and oxygen change their properties in water.

Properties of matter can be classified into two categories —

(i) Physical properties: It can be measured or observed without changing the identity or the composition of the substance.

Physical properties, such as colour, odour, melting point, boiling point, density, etc.,

(ii) Chemical properties: The measurement or observation of chemical properties requires a chemical change to occur.

Chemical properties, like composition, combustibility, reactivity with acids and bases, etc.

---

Measurement of physical properties :

Quantitative measurement of properties is reaquired for scientific investigation.

Many properties of matter, such as length, area, volume, etc., are quantitative in nature.

The International System of Units (SI) : The SI system has seven base units. These units pertain to the seven fundamental scientific quantities.

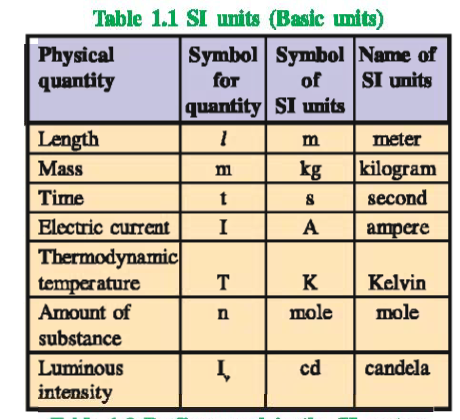
The other physical quantities, such as speed, volume, density, etc., can be derived from these quantities.

The SI system allows the use of prefixes to indicate the multiples or sub multiples of a unit.

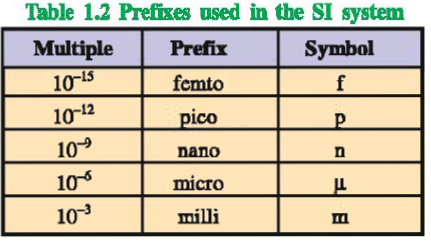
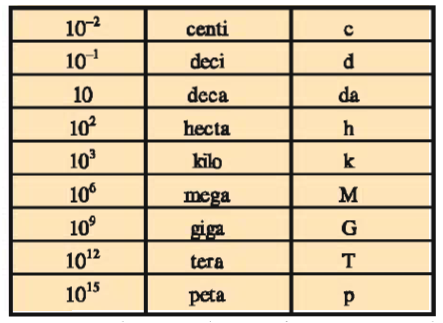
Definitions of some of the SI units and derived units are mentioned below :

Mass : Amount of matter present in a substance is called Mass. Its SI unit is kilogram.

The mass of a substance can he determined in the laboratory by using an analytical balance.
However, its fractions-gram, milligram, micro-gram are used in laboratories due to the smaller amounts of chemicals used in chemical reactions.

---

Volume (Derived unit) : Volume is the amont of space occupied by a substance. It has the units of (length)³.

SI system, volume has units of m³  . In chemistry laboratories, smaller volumes are used. Hence, volume is often denoted in cm³ or dm³ units.

A common unit, litre (L) which is not an SI unit, is used for measurement of volume of liquids.
1 L = 1000 mL , 1000 cm³ = 1 dm³

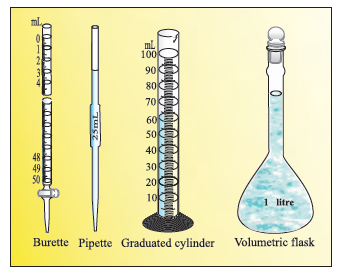
In the laboratory, the volume of liquids or solutions can be measured by graduated cylinder, burette, pipette, etc.

A volumetric flask is used to prepare a known volume of a solution.

---

Density : Density of a substance is its amount of mass per unit volume.

Density = \(\frac{mass}{volume}\)

SI unit of density = \(\frac{kg}{m^3}\) = \(kgm^{-3}\)

This unit is quite large and a chemist often expresses density in g cm^–3, where mass is expressed in gram and volume is expressed in cm³.

Density of a substance tells us about how closely its particles are packed. If density is more, it means particles are more closely packed.

---

Temperature : There are three common scales to measure temperature — °C (degree celsius), °F (degree fahrenheit) and K (kelvin). Here, K is the SI unit.

The temperatures on two scales are related to each other by the following relationship:

°F = \(\frac{9}{5}\) (°C) +32

The kelvin scale is related to celsius scale as follows:

K = °C + 273.15

It is interesting to note that temperature below 0 °C (i.e., negative values) are possible in Celsius scale but in Kelvin scale, negative temperature is not possible.

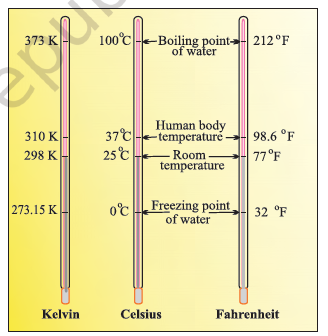
Thermometers using different temperature scales

---

Length :SI unit of length is meter. 

Meter : The distance travelled by light in vacuum in time interval of 1/299,792,458 second is called 1 meter.

---

Scientific Notation :
In which any number can be represented in the form N × 10ⁿ (Where n is an exponent having positive or negative values and N can vary between 1 to 10).

e.g. We can write 232.508 as 2.32508 x10² in scientific notation. Similarly, 0.00016 can be written as 1.6 x 10^–4.

Precision refers to the closeness of various measurements for the same quantity.

Accuracy is the agreement of a particular value to the true value of the result

Significant Figures :
The reliability of a measurement is indicated by the number of digits used to represent it. To express it more accurately we express it with digits that are known with certainty. These are called as Significant figures.

They contain all the certain digits plus one doubtful digit in a number. 

Rules for Determining the Number of Significant Figures :

All non-zero digits are significant. For example, 6.9 has two significant figures, while 2.16 has three significant figures. The decimal place does not determine the number of significant figures.

A zero becomes significant in case it comes in between non zero numbers. For example, 2.003 has four significant figures, 4.02 has three significant figures.

Zeros at the beginning of a number are not significant. For example, 0.002 has one significant figure while 0.0045has two significant figures.

All zeros placed to the right of a number are significant. For example, 16.0 has three significant figures, while 16.00 has four significant figures.

Zeros at the end of a number without decimal point are ambiguous.

In exponential notations, the numerical portion represents the number of significant figures. For example, 0.00045 is expressed as 4.5 x 10^-4 in terms of scientific notations. The number of significant figures in this number is 2, while in Avogadro's number (6.023 x 10²³) it is four.

The decimal point does not count towards the number of significant figures. 

For example, the number 345601 has six significant figures but can be written in different ways, as 345.601 or 0.345601 or 3.45601 all having same number of significant figures.

Retention of Significant Figures - Rounding off Figures :

The rounding off procedure is applied to retain the required number of significant figures.
1. If the digit coming after the desired number of significant figures happens to be more than 5, the preceding significant figure is increased by one, 4.317 is rounded off to 4.32.

2. If the digit involved is less than 5, it is neglected and the preceding significant figure remains unchanged, 4.312 is rounded off to 4.31.

3. If the digit happens to be 5, the last mentioned or preceding significant figure is increased by one only in case it happens to be odd. In case of even figure, the preceding digit remains unchanged. 8.375 is rounded off to 8.38 while 8.365 is rounded off to 8.36.

Dimensional Analysis : During calculations generally there is a need to convert units from one system to other. This is called factor label method or unit factor method or dimensional analysis.

For example- 5 feet and 2 inches (height of an Indian female) is to converted in SI unit
1 inch = 2.54 x 10^-2 m

1= \(\frac{2.54 × 10^2 m}{1 \,inch}\)

5 Feet and 2 inch = 62 inch = 62 inch × \(\frac{2.54 × 10^2 m}{1 \,inch}\) = 1.58 m

LAWS OF CHEMICAL COMBINATIONS : When two or more substances react chemically a compound is formed.

The following are the laws which govern the formation of chemical compounds.

Law of Conservation of Mass: Matter can neither be created nor destroyed.” This law was put forth by Antoine Lavoisier in 1789.

Dalton’s Atomic theory : “Matter is made up of small indivisible particles.” These smallest indivisible particles are called atoms.

In 1808, Dalton published A New System of Chemical Philosophy in which he proposed law of chemical combination which provides explanation for existence of atom. Dalton’s assumptions are as follows:

1-All elements are made up of smallest particles called atoms. Atom is indivisible

2- All the atoms of a given element are identical but are different from those of other elements.

3- All the atoms of a given element have identical properties including identical mass. Atoms of different elements differ in mass.

4- Compounds are formed when atoms of different elements combine in a fixed ratio. Atoms present in a compound have definite composition.

5- AU the atoms of a given element are identical in mass.

There is no importance of Dalton s law with reference to nuclear reactions and discovery of isotopes because Dalton’s view that atom is indivisible was found wrong. Atom is composed of fundamental particles like
proton, electron and neutron.

---

Law of Definite Proportions : A given compound always contains exactly the same proportion of elements by weight.

This law was given by, a French chemist, Joseph Proust.

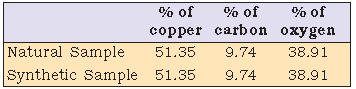
irrespective of the source, a given compound always contains same elements combined together in the same
proportion by mass.

The validity of this law has been confirmed by various experiments. It is sometimes also referred to as Law of
Definite Composition.

Water (H₂O) always contains 2.016 g of hydrogen and 16.0 g of oxygen.

Law of Multiple Proportions : If two elements can combine to form more than one compound, the
masses of one element that combine with a fixed mass of the other element, are in the ratio of small whole numbers.

This law was proposed by Dalton in 1803

example, hydrogen combines with oxygen to form two compounds, namely, water and hydrogen peroxide.
Hydrogen + Oxygen → Water
2g + 16g = 18g
Hydrogen + Oxygen → Hydrogen Peroxide
2g  + 32g = 34g
Here, the masses of oxygen (i.e., 16 g and 32 g),

Here, the masses of oxygen (i.e., 16 g and 32 g), which combine with a fixed mass of hydrogen (2g) bear a simple ratio, i.e., 16:32 or 1: 2.

Gay Lussac’s Law of Gaseous Volumes : When gases combine or are produced in a chemical reaction they do so in a simple ratio by volume, provided all gases are at the same temperature and pressure.

Thus, 100 mL of hydrogen combine with 50 mL of oxygen to give 100 mL of water vapour.
Hydrogen + Oxygen → Water
100 mL  + 50 mL = 100 mL
Thus, the volumes of hydrogen and oxygen which combine (i.e., 100 mL and 50 mL) bear a simple ratio of 2:1.

The Gay Lussac’s law was explained properly by the work of Avogadro in 1811.

---

Avogadro Law (In 1811, Given by Avogadro) : According to this law equal volumes of gases at the same temperature and pressure should contain equal number of molecules.

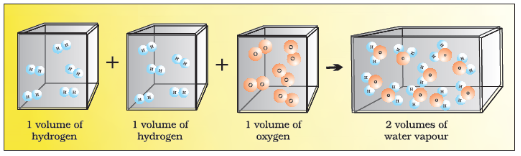
Consider  the reaction of hydrogen and oxygen to produce water, we see that two volumes of hydrogen combine with one volume of oxygen to give two volumes of water without leaving any un-reacted oxygen.

---

Dalton's Atomic Theory :

All substances are made up of tiny, indivisible particles called atoms.

Atoms of the same element are identical in shape, size, mass and other properties.

Atoms of different elements are different in all respects.

Atom is the smallest unit that takes part in chemical combinations.

Atoms combine with each other in simple whole number ratios to form compound atoms called molecules.

Atoms cannot be created, divided or destroyed during any chemical or physical change.

Atoms and Molecules :
The smallest particle of an element, which may or may not have independent existence is called an atom, while the smallest particle of a substance which is capable of independent existence is called a molecule.

Molecules are classified as homoatomic and heteroatomic.

Homoatomic molecules are made up of the atoms of the same element 

Heteroatomic molecules are made up of the atoms of the different element have different atomicity (number of atoms in a molecule of an element) like monoatomic, diatomic, triatomic and polyatomic.

Atomic Mass Unit (amu) :
One atomic mass unit is defined as a mass exactly equal to one twelfth the mass of one carbon -12 atom.

Carbon-12 is one of the isotopes of carbon and can be represented as ¹²C.

And 1 amu = 1.66056×10^–24 g. - masses of all other atoms are given relative to this standard.

Mass of an atom of hydrogen = 1.6736×10^–24 g

Thus, in terms of amu, the mass of hydrogen atom

= \(\frac{mass\, of\, atom}{1/12\, mass\, of\, carbon\, atom}\)

= \(\frac{1.6736×10^{-24}}{1.66056×10^{-24}}\)

= 1.0078 amu = 1.0080 amu

Today, ‘amu’ has been replaced by ‘u’ which is known as unified mass.

Atomic Mass :
Atomic mass of an element is defined as the average relative mass of an atom of an element as compared to the mass of an atom of carbon -12 taken as 12.

From the above data, the average atomic mass of carbon will come out to be:

(0.98892) (12 u) + (0.01108) (13.00335 u) +  (2 × 10–12) (14.00317 u) = 12.011 u

In the periodic table of elements, the atomic masses mentioned for different elements actually represent their average atomic masses.

Gram Atomic Mass : The quantity of an element whose mass in grams is numerically equal to its atomic mass.

In simple terms, atomic mass of an element expressed in grams is the gram atomic mass or gram atom.

For example, the atomic mass of oxygen = 16 amu
Therefore gram atomic mass of oxygen = 16 g

Molecular Mass :Molecular mass of a substance is defined as the average relative mass of its molecule as compared to the mass of an atom of C-12 taken as 12.

It expresses as to how many times the molecule of a substance is heavier than 1/12th of the mass of an atom of carbon.

For example, a molecule of carbon dioxide is 44 times heavier than 1/12th of the mass of an atom of carbon. Therefore the molecular mass of CO₂ is 44 amu.

It is obtained by adding the atomic masses of all the atoms present in one molecule.

Molecular mass of methane,
(CH4) = (12.011 u) + 4 (1.008 u)
= 16.043 u
Similarly, molecular mass of water (H2O)
= 2 × atomic mass of hydrogen + 1 × atomic mass of oxygen
= 2 (1.008 u) + 16.00 u
= 18.02 u

Gram Molecular Mass : A quantity of substance whose mass in grams is numerically equal to its molecular mass is called gram molecular mass.

In simple terms, molecular mass of a substance expressed in grams is called gram molecular mass.

e.g., the molecular mass of oxygen = 32 amu
Therefore, gram molecular mass of oxygen = 32 g

Formula Mass : Sum of atomic masses of the elements present in one formula unit of a compound. It is used for the ionic compounds.

The formula mass of sodium chloride is :  atomic mass of sodium + atomic mass of chlorine
= 23.0 u + 35.5 u = 58.5 u

Mole Concept and Molar Masses : Mole is defined as the amount of a substance, which contains the same number of chemical units (atoms, molecules, ions or electrons) as there are atoms in exactly 12 grams of pure carbon-12.

A mole represents a collection of 6.022 x10²³( Avogadro's number) chemical units. Avogadro number denoted by N_A

many entities (atoms, molecules or any other particle) constitute one mole of a particular substance.

1 mol of hydrogen atoms = 6.022×10²³ atoms
1 mol of water molecules = 6.022×10²³ water molecules
1 mol of sodium chloride = 6.022 × 10²³ formula units of sodium chloride

The mass of one mole of a substance in grams is called its molar mass.

The molar mass in grams is numerically equal to atomic/molecular/ formula mass in u.
Molar mass of water = 18.02 g mol^-1
Molar mass of sodium chloride = 58.5 g mol^-1

Molar Volume : The volume occupied by one mole of any substance is called its molar volume. It is denoted by V_m.

One mole of all gaseous substances at 273 K temperature and 1 atm pressure occupies a volume equal to 22.4 litre or 22,400 mL. The unit of molar volume is litre per mol or milliliter per mol

Percentage Composition : The mass percentage of each constituent element present in any compound is called its percentage composition

Mass % of the element =\(\frac{Mass\, of\, element\, in\, 1\, molecule\, of\, the\, compound}{ Molecular\, mass\, of\, the\, compound} \) × 100

Example : 
(i) Water (H₂O). Since water contains hydrogen and oxygen, the percentage composition of both these elements can be calculated as follows:

Mass % of an element = \(\frac{Mass\, of\, element\, in\, the\, compound}{ Molar\, mass\, of\, the\, compound} \) × 100

Molar mass of water = 18.02 g

Mass % of hydrogen = \(\frac{2 × 1.0008}{18.02}\) × 100 = 11.18 

Mass % of oxygen = \(\frac{16.00}{18.02}\) × 100 = 88.79 

(ii) What is the percentage of carbon, hydrogen and oxygen in ethanol?

Molecular formula of ethanol is: C₂H₅OH

Molar mass of ethanol is: (2×12.01 + 6×1.008 + 16.00) g = 46.068 g

Mass per cent of carbon = \(\frac{24.02g}{46.068g}\) × 100 = 52.14%

Mass per cent of hydrogen = \(\frac{6.048g}{46.068g}\) × 100 = 13.13%

Mass per cent of oxygen = \(\frac{16.00g}{46.068g}\) × 100 = 4.73%

---

Empirical Formula and Molecular Formula—
An empirical formula represents the simplest whole number ratio of various atoms present in a compound.

E.g. CH is the empirical formula of benzene.

The molecular formula shows the exact number of different types of atoms present in a molecule of a compound.

E.g. C6H6 is the molecular formula of benzene.

Relationship between empirical and molecular formulae

The two formulas are related as Molecular formula = n x empirical formula

n= \(\frac{Molecular\, mass}{ Emperical \, formula \, mass} \)

Example :

(i) A compound contains 4.07% hydrogen, 24.27% carbon and 71.65% chlorine. Its molar mass is 98.96 g. What are its empirical and molecular formulas?

Solution :
Step 1. Conversion of mass per cent to grams

Since we are having mass per cent, it is convenient to use 100 g of the compound as the starting material.

Thus, in the 100 g sample of the above compound, 4.07g hydrogen, 24.27g carbon and 71.65g chlorine are present.

Step 2. Convert into number moles of each element

Divide the masses obtained above by respective atomic masses of various elements. This gives the number of moles
of constituent elements in the compound.

Moles of hydrogen = \(\frac{4.07g}{1.008g}\) × 100 = 4.04

Moles of carbon = \(\frac{24.27g}{12.01g}\) × 100 = 2 021

Moles of chlorine = \(\frac{71.65g}{35.453g}\) × 100 = 2 021

Step 3. Divide each of the mole values obtained above by the smallest number amongst them

Since 2.021 is smallest value, division by it gives a ratio of 2:1:1 for H:C:Cl .

In case the ratios are not whole numbers, then they may be converted into whole number by multiplying by the suitable coefficient.

Step 4. Write down the empirical formula by mentioning the numbers after writing the symbols of respective elements

CH₂Cl is, thus, the empirical formula of the above compound.

Step 5. Writing molecular formula

(a) Determine empirical formula mass by adding the atomic masses of various atoms present in the empirical formula.

For CH₂Cl, empirical formula mass is
12.01 + (2 × 1.008) + 35.453 = 49.48 g

(b) Divide Molar mass by empirical formula mass

n= \(\frac{Molecular\, mass}{ Emperical \, formula \, mass} \) = \(\frac{98.96g}{49.48g}\) = 2

(c) Multiply empirical formula by n obtained above to get the molecular formula

Empirical formula = CH₂Cl, n = 2. Hence molecular formula is C₂H₄Cl₂.

Stoichiometry: deals with the calculation of masses (sometimes volumes also) of the reactants and the products involved in a chemical reaction.

Information is available from the balanced chemical equation of a given reaction.

Example :

Combustion of methane : A balanced equation for this reaction is

CH₄ (g) + 2O₂ (g) → CO₂ (g) + 2 H₂O (g) : Here, methane and dioxygen are called reactants and carbon dioxide and water are called products.

Note that all the reactants and the products are gases in the above reaction and this has been indicated by letter (g) in the brackets next to its formula.

Similarly, in case of solids and liquids, (s) and (l) are written respectively.

The coefficients 2 for O₂ and H₂O are called stoichiometric coefficients.

Similarly the coefficient for CH₄ and CO₂ is one in each case.

They represent the number of molecules (and moles as well) taking part in the reaction or formed in the reaction.

Thus, according to the above chemical reaction,

• One mole of CH₄(g) reacts with two moles of O₂(g) to give one mole of CO₂(g) and two moles of H₂O(g)

• One molecule of CH₄(g) reacts with 2 molecules of O₂(g) to give one molecule of CO₂(g) and 2 molecules of H₂O(g)

• 22.7 L of CH₄(g) reacts with 45.4 L of O₂ (g) to give 22.7 L of CO₂ (g) and 45.4 L of H₂O(g)

• 16 g of CH₄ (g) reacts with 2×32 g of O₂ (g) to give 44 g of CO₂ (g) and 2×18 g of H₂O (g).

From these relationships, the given data can be interconverted as follows: 

\(\frac{Mass}{Volume}\) = Density

Chemical Equation: Shorthand representation of a chemical change in terms of symbols and formulae of the substances involved in the reaction is called chemical equation..

The substances that react among themselves to bring about the chemical changes are known as reactants, whereas the substances that are produced as a result of the chemical change, are known as products.

Limiting Reagent- The reactant which gets consumed first or limits the amount of product formed is known as limiting reagent

Reactions in Solutions-- The concentration of a solution can be expressed in any of the following ways.

1- Mass Percent is the mass of the solute in grams per 100 grams of the solution.

Mass % of the solute = \(\frac{Mass\, of\, the\, solute}{Mass\, of\, the\, solution}\) × 100

A 5 % solution of sodium chloride means that 5 g of NaCl is present in 100 g of the solution.

2- Volume percent is the number of units of volume of the solute per 100 units of the volume of solution.

Volume % of the solute = \(\frac{Volume\, of\, the\, solute}{Volume\, of\, the\, solution}\) × 100

A 5 % (v/v) solution of ethyl alcohol contains 5 cm³ of alcohol in 100 cm³ of the solution.

3- Molarity of the solution is defined as the number of moles of solute dissolved per litre (dm³) of the solution. It isdenoted by the symbol M. Measurements in Molarity can change with the change in temperature because solutions expand or contract accordingly. 

Molarity of the solution = \(\frac{No.\, of\, moles \, of\, the\, solute}{Volume\, of\, the\, solution\, in \, ltr}\) = \(\frac{n}{V}\)

The Molarity of the solution can also be expressed in terms of mass and molar mass.

Molarity of the solution = \(\frac{Mass \, of\, the\, solute}{Molar \,Mass \, of\, the\, solute × Volume\, of\, the\, solution\, in \, ltr}\)

In terms of weight, molarity of the substance can be expressed as:

Molarity = \(\frac{W(g)}{M(g\, mol^{-1}) × V(ltr) }\)

= \(\frac{W}{M × V}\) mol/L

Molarity equation : To calculate the volume of a definite solution required to prepare solution of other molarity, the following equation is used:

M₁V₁ = M₂V₂, where M1= initial molarity, M₂= molarity of the new solution, V₁= initial volume and V₂= volume of the new solution.

4. Molality- Molality is defined as the number of moles of solute dissolved per 1000 g (1 kg) of solvent. Molality is expressed as 'm'.

Molality = \(\frac{Moles \, of\, the\, solute}{Wt \, of\, the\, solvent \, in \, gm}\) × 1000

5. Mole Fraction is the ratio of number of moles of one component to the total number of moles (solute and solvents) present in the solution. It is expressed as 'x'.

Mole fraction of the solute =\(\frac{Moles \, of\, the\, solute}{Moles \, of\, solute \, + Moles \,of\, solvent}\) 

Mole fraction of the solvent = \(\frac{Moles \, of\, the\, solvent}{Moles \, of\, solute \, + Moles \,of\, solvent}\) 

Mole fraction of the solute + Mole fraction of solvent = 1

A balanced chemical equation has the same number of atoms of each element on both sides of the equation.

Many chemical equations can be balanced by trial and error.

4 Fe(s) + 3O₂(g) =  2Fe₂O₃(s) ..... (a) balanced equation

2 Mg(s) + O₂(g) =  2MgO(s) ..... (b) balanced equation

P₄(s) + O₂ (g) =  P₄O₁₀(s) .....  (c) unbalanced equation

Equations (a) and (b) are balanced, equation (c) is not balanced.

In  equation (c), phosphorus atoms are balanced but not the oxygen atoms. To balance it, place the coefficient 5 on
the left of oxygen.

P₄(s) + 5O₂ (g) =  P₄O₁₀(s) .............balanced equation

All equations that have correct formulas for all reactants and products can be balanced.

Always remember that subscripts in formulas of reactants and products cannot be changed to balance an equation.

Steps to balance the equation :

Step 1 : Write down the correct formulas of reactants and products.

Step 2 : Balance the number of atoms of each element.

Step 3 : Verify that the number of atoms of each element is balanced in LHS and RHS of the final equation

Chemistry, as we understand it today is not a very old discipline. People in ancient India, already had the knowledge of many scientific phenomenon much before the advent of modern science. They applied the knowledge in various walks of life.

The study of chemistry is very important as its domain encompasses every sphere of life. Chemists study the properties and structure of substances and the changes undergone by them.

All substances contain matter, which can exist in three states – solid, liquid or gas.

The constituent particles are held in different ways in these states of matter and they exhibit their characteristic properties.

Matter can also be classified into elements, compounds or mixtures.

An element contains particles of only one type, which may be atoms or molecules.

The compounds are formed where atoms of two or more elements combine in a fixed ratio to each other.

Mixtures occur widely and many of the substances present around us are mixtures.

When the properties of a substance are studied, measurement is inherent. The quantification of properties requires a system of measurement and units in which the quantities are to be expressed. Many systems of measurement exist, of which the English and the Metric Systems are widely used.

The scientific community, however, has agreed to have a uniform and common system throughout the world, which is abbreviated as SI units (International System of Units).

Since measurements involve recording of data, which are always associated with a certain amount of uncertainty, the proper handling of data obtained by measuring the quantities is very important.

The measurements of quantities in chemistry are spread over a wide range of 10^–31 to 10⁺²³. Hence, a convenient system of expressing the numbers in scientific notation is used.

The uncertainty is taken care of by specifying the number of significant figures, in which the observations are reported.

The dimensional analysis helps to express the measured quantities in different systems of units. Hence, it is possible
to interconvert the results from one system of units to another.

The combination of different atoms is governed by basic laws of chemical combination
— these being the Law of Conservation of Mass, Law of Definite Proportions, Law of Multiple Proportions, Gay Lussac’s Law of Gaseous Volumes and Avogadro Law.

All these laws led to the Dalton’s atomic theory, which states that atoms are building blocks of matter.

The atomic mass of an element is expressed relative to 12C isotope of carbon, which has an exact value of 12u.

Usually, the atomic mass used for an element is the average atomic mass obtained by taking into account the natural abundance of different isotopes of that element.

The molecular mass of a molecule is obtained by taking sum of the atomic masses of different atoms present in a molecule. The molecular formula can be calculated by determining the mass per cent of different elements present
in a compound and its molecular mass.

The number of atoms, molecules or any other particles present in a given system are expressed in the terms of Avogadro constant (6.022 × 10²³). This is known as 1 mol of the respective particles or entities.

Chemical reactions represent the chemical changes undergone by different elements and compounds. A balanced chemical equation provides a lot of information.

The coefficients indicate the molar ratios and the respective number of particles taking part in a particular reaction.

The quantitative study of the reactants required or the products formed is called stoichiometry. Using stoichiometric calculations, the amount of one or more reactant(s) required to produce a particular amount of product can be determined and vice-versa.

The amount of substance present in a given volume of a solution is expressed in number of ways, e.g., mass per cent, mole fraction, molarity and molality.

Q(i) Calculate the amount of water (g) produced by the combustion of 16 g of methane.

Solution :
The balanced equation for the combustion of methane is :

CH₄ (g) + 2O₂ (g) →  CO₂ (g) + 2H₂O (g)

(i)16 g of CH₄ corresponds to one mole.

(ii) From the above equation, 1 mol of CH₄ (g) gives 2 mol of H₂O (g).

2 mol of water (H₂O) = 2 × (2+16) = 2 × 18 = 36 g

1 mol H₂O = 18 g H₂O ⇒ \(\frac{ 18 g\, H_2O}{1 mol \,H_2O}\) = 1

Hence, 2 mol H2O × \(\frac{ 18 g\, H_2O}{1 mol \,H_2O}\)

= 2 × 18 g H₂O = 36 g H₂O

---

Q(ii) How many moles of methane are required to produce 22g CO2 (g) after combustion?

Solution :
According to the chemical equation,

CH₄ (g) + 2O₂ (g) → CO₂ (g) + 2H₂O (g)

44g CO₂ (g) is obtained from 16 g CH₄ (g).

[∴ 1 mol CO₂(g) is obtained from 1 mol of CH₄(g)]

Number of moles of CO2 (g) = 22 g CO₂ (g) × \(\frac{ 1 mol\, CO_2(g)}{44 g\, CO_2 (g)}\)

= 0.5 mol CO₂ (g)

Hence, 0.5 mol CO₂ (g) would be obtained from 0.5 mol CH₄ (g)

or 0.5 mol of CH₄ (g) would be required to produce 22 g CO₂ (g).

---

Q(iii) 50.0 kg of N₂ (g) and 10.0 kg of H₂ (g) are mixed to produce NH₃ (g). Calculate the amount of NH₃ (g) formed. Identify the limiting reagent in the production of NH3 in this situation.

Solution :
A balanced equation for the above reaction is written as follows :

N₂ (g) + 3H₂ (g) ⇔  2NH₃ (g)

Calculation of moles :

Number of moles of N₂  = 50.00kg N₂ × _{\(\frac{ 1000(g)N_2}{1(kg)N_2}\) × \(\frac{ 1\,mol\,N_2}{28.0(g)N_2}\)}

= 17.86×10² mol
Number of moles of H₂ = 10.00kg H₂  × _{\(\frac{ 1000(g)H_2}{1(kg)H_2}\) × \(\frac{ 1\,mol\,H_2}{2.016(g)H_2}\)}

= 4.96×10³ mol

According to the above equation, 1 mol N₂ (g) requires 3 mol H₂ (g), for the reaction.

Hence, for 17.86×10² mol of N₂ , the moles of H₂ (g) required would be

= 17.86×10² mol of N₂ × _{\(\frac{ 3mole\, H_2 (g)}{1 mol\, N_2(g)}\)}

5.36 ×10³ mol H₂

But we have only 4.96×103 mol H₂.

Hence, dihydrogen is the limiting reagent in this case.

So, NH₃(g) would be formed only from that amount of available dihydrogen
i.e., 4.96 × 10³ mol

Since 3 mol H₂(g) gives 2 mol NH₃(g)

4.96×10³ mol H₂ (g) ×  _{\(\frac{ 2mole\, NH_3 (g)}{3 mol\, H_2(g)}\)}

= 3.30×10³ mol NH₃ (g)

3.30×10³ mol NH₃ (g) is obtained.

If they are to be converted to grams, it is done as follows :

1 mol NH₃ (g) = 17.0 g NH₃(g)

3.30 × 10³ mol NH₃ (g)  ×  _{\(\frac{ 17.0g\, NH_3 (g)}{1 mol\, NH_3(g)}\)}

3.30×10³×17 g NH₃ (g)

= 56.1×10³ g NH₃

= 56.1 kg NH₃

---

Q(iv) A solution is prepared by adding 2 g of a substance A to 18 g of water. Calculate the mass per cent of the solute.

Solution :

Mass per cent of A = _{\(\frac{ Mass \, of \, A}{Mass \, of \, solution}\) × 100}

=  _{\(\frac{ 2g }{2g \, of \, A \, + 18 \, g \, of \, water}\) × 100}

=  _{\(\frac{ 2g }{20g}\) × 100}

= 10%

---

Q(v) Calculate the molarity of NaOH in the solution prepared by dissolving its 4 g in enough water to form 250 mL of the solution.

Solution :
molarity (M)  = \(\frac{No.\, of\, moles \, of\, the\, solute}{Volume\, of\, the\, solution\, in \, ltr}\)

= \(\frac{Mass \, of \, NaOH/Molar \, mass \, of \ NaOH}{0.250L}\)

= \(\frac{4g/40g}{0.250L}\) = \(\frac{0.1 \, mole}{0.250L}\) 

= \(0.4mol^{-1}\)

= 0.4M

Note that molarity of a solution depends upon temperature because volume of a solution is temperature dependent

---

Q(vi) The density of 3 M solution of NaCl is 1.25 g mL^–1. Calculate the molality of the solution.

Solution:

M = 3 mol L^–1
Mass of NaCl in 1 L solution = 3 × 58.5 = 175.5 g

( The formula, such as NaCl, is used to calculate the formula mass instead of molecular mass as in the solid state sodium chloride does not exist as a single entity. Thus, the formula mass of sodium chloride is atomic mass of sodium + atomic mass of chlorine = 23.0 u + 35.5 u = 58.5 u)

Mass of  1L solution = 1000 × 1.25 = 1250 g
(since density = 1.25 g mL^–1)

Mass of water in solution = 1250 –175.5 = 1074.5 g

Molality = No. of moles of solute / Mass of solvent in kg

= 3 mol / .0745kg = 2.79 m

Often in a chemistry laboratory, a solution of a desired concentration is prepared by diluting a solution of known higher concentration.

The solution of higher concentration is also known as stock solution.

Note that the molality of a solution does not change with temperature since mass remains unaffected with  temperature.

---