Three such systems, the CGS system, the FPS (or British) system and the MKS system were in use extensively till recently.

The base units for length, mass and time in these systems were as follows :

• In CGS system they were centimetre, gram and second respectively.
• In FPS system they were foot, pound and second respectively.
• In MKS system they were metre, kilogram and second respectively.

The system of units which is at present internationally accepted for measurement is the Système Internationale
d’ Unites (French for International System of Units), abbreviated as SI.

The SI, with standard scheme of symbols, units and abbreviations, was developed and recommended  in 1971 for international usage in scientific, technical, industrial and commercial work.

SI Units : SI units used decimal system, conversions within the system are quite simple and convenient.
In SI, there are seven base units as given in Table.

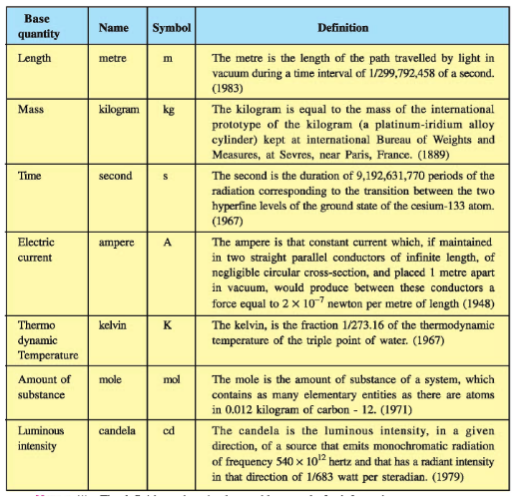
( The values mentioned here need not be remembered or asked in a test. They are given here only to indicate the extent of accuracy to which they are measured. )

Besides the seven base units, there are two more units (Supplementary Units)  that are defined for

(a) plane angle dθ as the ratio of length of arc ds to the radius r

(b) solid angle dΩ as the ratio of the intercepted area dA of the spherical surface,

Described about the apex O as the centre, to the square of its radius r, as shown in Fig. (a) and (b) respectively.

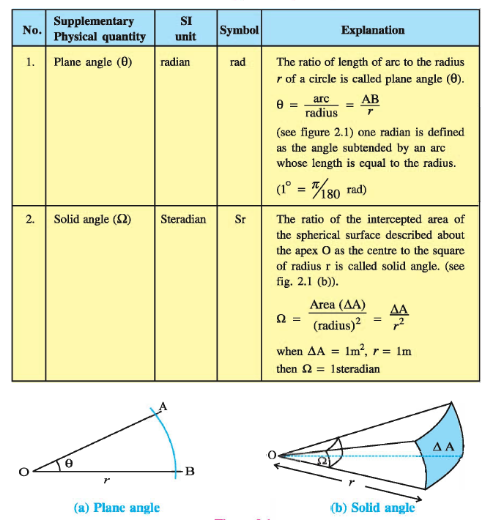
The unit for plane angle is radian with the symbol rad and the unit for the solid angle is steradian with the symbol sr.

Both these are dimensionless quantities.

Derived Units : All other units of different physical quantities can be expressed as a combination of these seven base units of SI system. Such units are called derived units.

A metre scale is used for lengths from 10^–3 m to 10² m.

A vernier callipers is used for lengths to an accuracy of 10^–4 m.

A screw gauge and a spherometer can be used to measure lengths as less as to 10^–5 m.

---

Measurement of Large Distances

Parallax method : To measure lengths beyond these ranges, we make use of some special indirect methods these method are called parallax method.

Large distances such as the distance of a planet or a star from the earth  measured with help of parallax method.

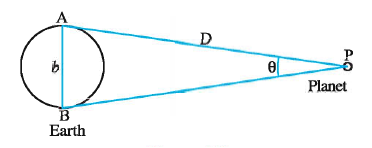
To measure the distance D of a far away planet P by the parallax method,

we observe it from two different positions (observatories) A and B on the Earth, separated by distance AB = b at the same time as shown in Fig. 2.2.

We measure the angle between the two directions along which the planet is viewed at these two points.

The ∠APB in Fig represented by symbol θ is called the parallax angle or parallactic angle.

the radius AP = BP

θ = \(\frac{arc}{radius}\)

Therefore arc = AB = b = radius X θ = D θ     .... where θ is in radians

Therefore D = \(\frac{b}{θ}\)

---

Example : (i)  Calculate the angle of 

(a) 1⁰ (degree)

(b) 1′ (minute of arc or arcmin) and

(c) 1″ (second of arc or arc second) in radians.

Use 360⁰=2π rad, 1⁰=60′ and  1′ = 60 ″

Answer :  (a) We have 360⁰ = 2π rad
∴ 1⁰ = 2π/ 360 =(π /180) rad = 1.745×10^–2 rad
(b) 1⁰ = 60′ = 1.745×10^–2 rad
1′ = 1.745×10^–2/ 60 = 2.908×10^–4 rad ; 2.91×10^–4 rad
(c) 1′ = 60″ = 2.908×10^–4 rad
1″ = 4.847×10^–6 rad ; 4.85×10^–6 rad

---

(ii)  A man wishes to estimate the distance of a nearby tower from him.
He stands at a point A in front of the tower C and spots a very distant object O in line with AC.

He then walks perpendicular to AC up to B, a distance of 100 m, and looks at O and C again.

Since O is very distant, the direction BO is practically the same as AO; but he finds the line of sight of C shifted from the original line of sight by an angle θ = 40⁰ (θ is known as ‘parallax’), estimate the distance of the tower C from his original position A.

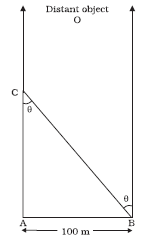Answer : We have, parallax angle θ = 40⁰
From Fig. , AB = AC tan θ
AC = AB/tanθ = 100 m/tan 40⁰
= 100 m/0.8391 = 119 m

---

(iii) The moon is observed from two diametrically opposite points A and B on Earth. The angle θ subtended at the moon by the two directions of observation is 1^o 54′ . Given the diameter of the Earth to be about 1.276 × 10⁷ m, compute the distance of the moon from the Earth.

Answer : We have θ = 1° 54′ = 114′

= (114 × 60)′′ × (4.85 ×10^-6 ) rad ...... since 1" = 4.85 ×10⁻⁶ rad.

= 3.32 × 10 ^-2 rad,

Also b = AB =1.276 ×10⁷ m

Hence from Eq. D = b /θ, we have the earth-moon distance,

D = b /θ

= 1.276 × 10 ⁷ / 3.32 × 10 ^-2

= 3.84 ×10 ⁸ m

(iv)  The Sun’s angular diameter is measured to be 1920". The distance D of the Sun from the Earth is 1.496 × 10¹¹ m. What is the diameter of the Sun ?

Answer : Sun’s angular diameter α = 1920"
= 1920  ×  4.85 × 10 ^-6 rad  ............ (1″= 4.85×10^–6 rad)
= 9.31×10⁻³ rad
Sun’s diameter
d =α D

= (9.31 × 10 ^-3 ) × (1.496 × 10¹¹ )m 
=1.39 ×10⁹ m

---

Measurement of Very Small Distances: Size of a Molecule

Very small distance like size of molecules, radius of atoms etc, cannot be measured with the help of instruments like vernier caliper, screw gauge, spherometer etc.

Even optical microscope cannot measure these distances. In optical microscopes cannot measure these distances.

In optical microscopes, visible light is used whose wavelength is of the order of 6 × 10^-7 m. Hence, we cannot see as object by an optical microscope whose dimension is less than 6 × 10^-7 m.

Visible light the range of wavelengths is from about 4000 Å to 7000 Å (1 angstrom = 1 Å = 10^-10 m)

Electron microscope is a device which can measure distance of the order of 10^-8m. In this microscope, we use an accelerated beam of electrons instead of visible light while focusing is done with the help of electric and magnetic fields.

Electron microscopes with a resolution of 0.6 Å have been built, can resolve atoms and molecules in a material.

Distance between molecules of crystals can be measured by x-ray diffraction experiments. Subatomic distances can be measured by alpha particle scattering experiments.

These are also some indirect methods for the measurement of microscopic distances. These methods may be used if only a rough estimate of small distances is desired. Two such methods are described below.

a) Avogadro’s Hypothesis: Because the atoms are spherical in shape, hence when a large number of atoms are put together, the vacant spaces are left between them and the actual volume occupied by the atoms in a substance is always less than the volume of that substance.

According to Avogadro’s hypothesis, “the actual volume occupied by the atoms in a certain mass of a substance is two-thirds the volume occupied by that mass of the substance”.

Example : Consider a monoatomic substance having mass m and volume V.

If M and N are molecular weight of the substance and Avagadro’s number respectively,

The number of atoms of the substance having mass m= N/M meter
Assuming that each atom is a sphere of radius r,

the volume occupied by atoms in the substance. V = (mN/M ) × (4/3)πr³

Because, according to Avogadro’s hypothesis, all the atoms in a given specimen of the substance occupy 2/3 rd the volume V of the substance

Therefore (4/3)πr³ X mN/M=(2/3)V=(2/3)m/ρ  (ρ = density of substance)
Or   r=(M/2πN ρ)^1/3
Thus, knowing the values of M, N and ρ, r can be calculated.

b) Molecular layer method:  It is a practical method for estimating the size of the molecule of a liquid.

The basic idea behind this method is to prepare a layer of one molecule thickness of a liquid on water. This method is quite adequate for the liquids whose molecules are quite big in size.

Oleic acid is a very good example of such liquid.

Estimating size of molecule of Oleic acid

The steps followed in determining the size of molecule are:

• Dissolve 1 cm³ of oleic acid in alcohol to make a solution of 20 cm³.
• Take 1 cm³ of above solution and dissolve in alcohol to make a solution of 20 cm³ Concentration of oleic acid in the solution will be (1/(20x20)) cm³.
• Sprinkle lycopodium powder on the surface of water in a trough and put one drop of above solution. The oleic acid in the solution will spread over water in a circular molecular thick film.
• Measure the diameter of the above circular film using below calculations.

If n –Number of drops of solution in water, V – Volume of each drop, t – Thickness of the film, A – Area of the film

Total volume of n drops of solution = nV cm³

Amount of Oleic acid in this solution = nV(\(\frac{1}{20×20}\)) cm³

Thickness of the film = t = Volume of the film / Area of the film

t =  \(\frac{nV}{20×20A} \)cm

---

Example :

(i) If the size of a nucleus (in the range of 10^–15 to 10^–14 m) is scaled up to the tip of a sharp pin, what roughly is the size of an atom ?

Assume tip of the pin to be in the range 10^–5m to 10^–4m.

Answer :   Here we are scaling up by a factor of 10¹⁰.

An atom roughly of size 10^–10 m will be scaled up to a size of 1 m.

Thus a nucleus in an atom is as small in size as the tip of a sharp pin placed at the centre of a sphere of radius about a metre long.

---

Range of Lengths : We also use certain special length units for short and large lengths. These are given in below table.

Special Length units

Unit name	Unit Symbol	Value in meters
fermi	f	10-15 m
Angstrom	Å	10-10m
Astronomical unit(average distance of sun from earth)	AU	1.496 X 1011 m
Light year(distance travelled by light in 1 year with velocity 3 X 108m/s)	ly	9.46 X 1011 m
Parsec(distance at which average radius of earth’s orbits subtends an angle of 1 arc second)	pc	3.08 x 1016 m

Measurement of Mass

Mass is usually measured in terms of kg but for atoms and molecules, unified atomic mass unit (u) is used.

1 unified atomic mass unit = u = 1/12 of the mass of an atom of carbon-12 isotope including mass of electrons =  (1.66 x 10^-27 kg)

Using balances to measure mass of  normal weights,

Mass of planets is measured using gravitational methods

Mass of atomic particles are measured using mass spectrograph (radius of trajectory is proportional to mass of charged particle moving in uniform electric and magnetic field).

Range of Mass

Object	Mass (kg)
Electron	10-30
Proton	10-27
Red Blood Cell	10-13
Dust particle	10-9
Rain drop	10-6
Mosquito	10-5
Grapes	10-3
Human	102
Automobile	103
Boeing 747 aircraft	108
Moon	1023
Earth	1025
Sun	1030
Milky way Galaxy	1041
Observable Universe	1055

Atomic clock. : Time is measured using a clock. As a standard,atomic standard of time is now used, which is measured by Cesium or Atomic clock.

• In Cesium clock, a second is equal to 9,192,631,770 vibrations of radiation from the transition between two hyperfine levels of cesium-133 atom.
• Cesium clock works on the vibration of cesium atom which is similar to vibrations of balance wheel in a regular wristwatch and quartz crystal in a quartz wristwatch.
• National standard time and frequency is maintained by 4 atomic clocks. Indian standard time is maintained by a Cesium clock at National Physical Laboratory (NPL), New Delhi.
• Cesium clocks are very accurate and the uncertainty is very low 1 part in 10¹³ which means not more than 3 μs are lost or gained in a year.

Fig: Range and order of time interval 

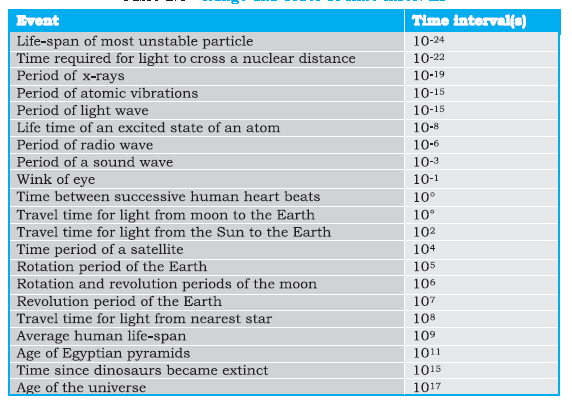
There is an interesting  coincidence between the numbers appearing in range Tables  Note that the ratio of the longest and shortest lengths of objects in our universe is about 1041. Interestingly enough, the ratio of the longest and shortest time intervals associated with the events and objects in our universe is also about 1041. The ratio of the largest and smallest masses of the objects in our universe is about (1041)2

Error :  The result of every measurement by any measuring instrument contains some uncertainty. This uncertainty is called error.

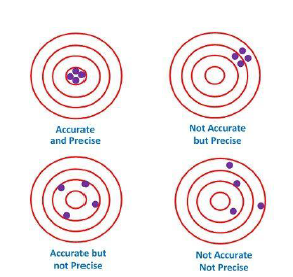
Accuracy and Precision:

Accuracy : refers to the closeness of a measured value to a standard or known value.

Example : If in lab you obtain a weight measurement of 3.2 kg for a given substance, but the actual or known weight is 4 kg, then your measurement is not accurate. In this case, your measurement is not close to the known value.

Precision : refers to the closeness of two or more measurements to each other.

Using the example above, if you weigh a given substance five times, and get 3.2 kg each time, then your measurement is very precise.

Precision is independent of accuracy. You can be very precise but inaccurate, as described above. You can also be accurate but imprecise.

For example, if on average, your measurements for a given substance are close to the known value, but the measurements are far from each other, then you have accuracy without precision.

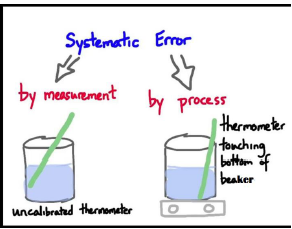
Systematic errors : The systematic errors are those errors that tend to be in one direction, either positive or negative.

Some of the sources of systematic errors are :

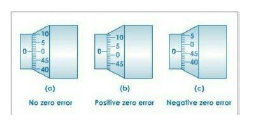
1- Instrument errors: These arise from imperfect design or calibration error in the instrument.

Worn off scale, zero error in a weighing scale are some examples of instrument errors.

2-Imperfection in experimental technique or procedure : To determine the temperature of a human body, a thermometer placed under the armpit will always give a temperature lower than the actual value of the body temperature.

Other external conditions (such as changes in temperature, humidity, wind velocity, etc.) during the experiment may systematically affect the measurement.

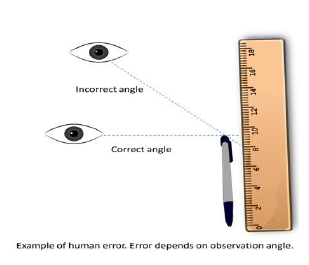
3- Personal errors : that arise due to an individual’s bias, lack of proper setting of the apparatus or individual’s carelessness in taking observations without observing proper precautions, etc.

For example, if you, by habit, always hold your head a bit too far to the right while reading the position of a
needle on the scale, you will introduce an error due to parallax.

4- Random errors : The random errors are those errors, which occur irregularly and hence are random with respect to sign and size.

These can arise due to random and unpredictable fluctuations in experimental conditions, like temperature, voltage supply, mechanical vibrations, personal errors etc.

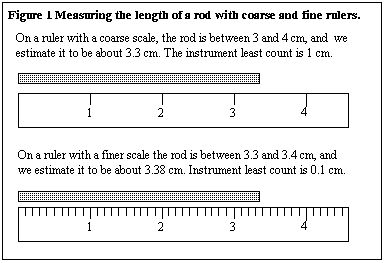
Smallest value that can be measured by the measuring instrument is called its least count.

5- Least count error : is the error associated with the resolution or the least count of the instrument.

Least count errors can be minimized by using instruments of higher precision/resolution and improving experimental techniques (taking several readings of a measurement and then taking a mean).

• A vernier callipers has the least count as 0.01 cm; a spherometer may have a least count of 0.001 cm.

---

Absolute Error, Relative Error and Percentage Error.

Errors in a series of Measurements

Suppose the values obtained in several measurement are a₁, a₂, a₃, …, a_n.

Arithmetic mean, a_mean = \(a_1, a_2, a_3, …, a_n \over n\) =

• Absolute Error: The magnitude of the difference between the true value of the quantity and the individual measurement value is called absolute error of the measurement. It is denoted by |Δa| (or Mod of Delta a). The mod value is always positive even if Δa is negative. The individual errors are:

Δa₁ = a_mean - a₁,  Δa₂ = a_mean - a₂,   ……. , Δa_n =  a_mean – a_n

• Mean absolute error is the arithmetic mean of all absolute errors. It is represented by Δa_mean.

Δa_mean = (|Δa₁| + |Δa₂| +|Δa₃| + …. +|Δa_n|) / n =

For single measurement, the value of ‘a’ is always in the range a_mean± Δa_mean

So, a =  a_mean ± Δa_mean Or  a_mean - Δa_mean< a <a_mean + Δa_mean

• Relative Error: It is the ratio of mean absolute error to the mean value of the quantity measured.

Relative Error =   \(Δa_{mean} \over a_{mean}\)

• Percentage Error: It is the relative error expressed in percentage. It is denoted by δa.

δa = \(Δa_{mean} \over a_{mean}\) x 100%

Combinations of Errors

If a quantity depends on two or more other quantities, the combination of errors in the two quantities helps to determine and predict the errors in the resultant quantity. There are several procedures for this.

Suppose two quantities A and B have values as A ± ΔA and B ± ΔB.  Z is the result and ΔZ is the error due to combination of A and B.

Criteria	Sum or Difference	Product	Raised to Power
Resultant value Z	Z = A ± B	Z = AB	Z = Ak
Result with error	Z ± ΔZ = (A ± ΔA) + (B ± ΔB)	Z ± ΔZ = (A ± ΔA) (B ± ΔB)	Z ± ΔZ = (A ± ΔA)k
Resultant error range	± ΔZ = ± ΔA ± ΔB	ΔZ/Z = ΔA/A ± ΔB/B
Maximum error	ΔZ = ΔA + ΔB	ΔZ/Z = ΔA/A + ΔB/B	ΔZ/Z = k(ΔA/A)
Error	Sum of absolute errors	Sum of relative errors	k times relative error

Hence the rule :

1- When two quantities are added or subtracted, the absolute error in the final result is the sum of the absolute errors in the individual quantities.

2-When two quantities are multiplied or divided, the relative error in the result is the sum of the relative errors in the multipliers.

3-The relative error in a physical quantity raised to the power k is the k times the relative error in the individual
quantity.

Example (i) Two clocks are being tested against a standard clock located in a national laboratory. At 12:00:00 noon by the standard clock, the readings of the two clocks are :

	Clock 1	Clock 2
Monday	12:00:05	10:15:06
Tuesday	12:01:15	10:14:59
Wednesday	11:59:08	10:15:18
Thursday	12:01:50	10:15:07
Friday	11:59:15	10:14:53
Saturday	12:01:30	10:15:24
Sunday	12:01:19	10:15:11

If you are doing an experiment that requires precision time interval measurements, which of the two clocks will you prefer ?

Answer :  The range of variation over the seven days of observations is 162 s for clock 1, and 31 s for clock 2.

The average reading of clock 1 is much closer to the standard time than the average reading of clock 2.

The important point for clock 1 is that a clock’s zero error is not as significant for precision work as its variation, because a ‘zero-error’ can always be easily corrected.

Hence clock 2 is to be preferred to clock 1.

---

(ii) We measure the period of oscillation of a simple pendulum. In successive measurements, the readings turn out to be 2.63 s, 2.56 s, 2.42 s, 2.71s and 2.80 s. Calculate the absolute errors, relative error or percentage error.

The mean period of oscillation of the pendulum
T = \(\frac{2.63 + 2.56 + 2.42 + 2.71+ 2.80}{5}\) s
= \(\frac{13.12}{5}\) s

= 2.624 s

T_mean = 2.62 s

As the periods are measured to a resolution of 0.01 s, all times are to the second decimal; it is proper to put this mean period also to the second decimal.

The absolute errors in the measurements are
2.63 s – 2.62 s = 0.01 s = ΔT₁
2.56 s – 2.62 s = – 0.06 s = ΔT2
2.42 s – 2.62 s = – 0.20 s = = ΔT3
2.71 s – 2.62 s = 0.09 s = ΔT4
2.80 s – 2.62 s = 0.18 s = ΔT5

Note that the errors have the same units as the quantity to be measured.

The arithmetic mean of all the absolute errors (for arithmetic mean, we take only the magnitudes) is

Mean absolute error = ΔΤ_mean = \(\frac{0.01+ 0.06+0.20+0.09+0.18}{5}\)s

.              = 0.11 s

That means, the period of oscillation of the simple pendulum is (2.62 ± 0.11) s

i.e. it lies  between (2.62 + 0.11) s and (2.62 – 0.11) s or between 2.73 s and 2.51 s.

As the arithmetic mean of all the absolute errors is 0.11 s, there is already an error in the tenth of a second.
Hence there is no point in giving the period to a hundredth. A more correct way will be to write

T = 2.6 ± 0.1 s

Note that the last numeral 6 is unreliable, since it may be anything between 5 and 7.

We indicate this by saying that the measurement has two significant figures. In this case, the two significant figures are 2, which is reliable and 6, which has an error associated with it.

( You will learn more about the significant figures in next section .)

For this example, the relative error or the percentage error is

Relative error =  \(\frac{0.1}{2.6}\)

Percentage error = δa = \(\frac{0.1}{2.6}\) × 100 = 4%

---

(iii) The temperatures of two bodies measured by a thermometer are t1 = 20 ⁰C ± 0.5 ⁰C and t2 = 50 ⁰C ± 0.5 ⁰C. Calculate the temperature difference and the error their in.

Answer : t′ = t2–t1 = (50 ⁰C±0.5 ⁰C)– (20⁰C±0.5 ⁰C)
t′ = 30 ⁰C ± 1 ⁰C

---

(iv) The resistance R = V/I where V = (100 ± 5)V and I = (10 ± 0.2)A. Find the percentage error in R.

Answer : The percentage error in V is 5% and in I it is 2%.

The total error in R would therefore be 5% + 2% = 7%.

---

(v) Two resistors of resistances R₁ = 100 ±3 ohm and R₂ = 200 ± 4 ohm are connected (a) in series, (b) in parallel. Find the equivalent resistance of the (a) series combination, (b) parallel combination.

Use for (a) the relation R =R₁ + R₂, and for

(b) \(\frac{1}{R'}\) = \(\frac{1}{R_1}\) + \(\frac{1}{R_2}\)  and

\(\frac{ΔR'}{R'^2}\) = \(\frac{ΔR_1}{(R_1)^2}\) + \(\frac{ΔR_2}{(R_2)^2}\)

Answer: (a) The equivalent resistance of series combination

R =R₁ + R₂ = (100 ± 3) ohm + (200 ± 4) ohm

.   = 300 ± 7 ohm.

(b) The equivalent resistance of parallel combination

R' = \(\frac{R_1R_2}{R_1 + R_2}\)

= \(\frac{(100)(200) }{(100) +(200)}\)

= \(\frac{200}{3}\)

= 66.7 ohm

Then, from \(\frac{1}{R'}\) = \(\frac{1}{R_1}\) + \(\frac{1}{R_2}\)

We get \(\frac{ΔR'}{R'^2}\) = \(\frac{ΔR_1}{(R_1)^2}\) + \(\frac{ΔR_2}{(R_2)^2}\)

ΔR' = (R'²) (\(\frac{ΔR_1}{(R_1)^2}\)) + (R'²) (\(\frac{ΔR_2}{(R_2)^2}\))

= (\(\frac{66.7}{100}\))² (3) +  (\(\frac{66.7}{200}\))² (4)

= 1.8

Then, R′ = 66.7 ±1.8 ohm
(Here, ΔR is expresed as 1.8 instead of 2 to keep in confirmity with the rules of significant figures.)

---

(vi) Find the relative error in Z, if Z = A⁴B^1/3/CD^3/2.

Answer : The relative error in Z is

ΔZ/Z = 4(ΔA/A) +(1/3) (ΔB/B) + (ΔC/C) + (3/2) (ΔD/D).

---

(vii) The period of oscillation of a simple pendulum is T = \(2π\sqrt{L/g}\)
Measured value of L is 20.0 cm known to 1 mm accuracy and time for 100 oscillations of the pendulum is found to be 90 s using a wrist watch of 1 s resolution.

What is the accuracy in the determination of g ?

Answer : g = 4π²L/T²
Here, T = t/n  and  ΔT = Δt/n

Therefore, ΔT/T = Δt/t

The errors in both L and t are the least count errors. Therefore,
(Δg/g) = (ΔL/L) + 2(ΔT/T )

= \(\frac{0.1}{20.0}\) + 2(\(\frac{1}{90}\)) = 0.032

Thus, the percentage error in g is
100 (Δg/g) = 100(ΔL/L) + 2 × 100 (ΔT/T )

= 100 x 0.032
= 3%

Significant figures : Every measurement results in a number that includes reliable digits and uncertain digits. Reliable digits plus the first uncertain digit are called significant digits or significant figures.These indicate the precision of measurement which depends on least count of measuring instrument.

A choice of change of different units does not change the number of significant digits or figures in a measurement.

Example: (i) The length 2.308 cm has four significant figures. But in different units, the same value can be written as 0.02308 m or 23.08 mm or 23080 μm.
All these numbers have the same number of significant figures (digits 2, 3, 0, 8), namely four.
This shows that the location of decimal point is of no consequence in determining the number of significant figures.

(ii) Period of oscillation of a pendulum is 1.62 s. Here 1 and 6 are reliable and 2 is uncertain. Thus, the measured value has three significant figures.

The example gives the following rules :

• All the non-zero digits are significant.
• All the zeros between two non-zero digits are significant, no matter where the decimal point is, if at all.
• If the number is less than 1, the zero(s) on the right of decimal point but to the left of the first non-zero digit are not significant. [In 0.00 2308, the underlined zeroes are not significant].
• The terminal or trailing zero(s) in a number without a decimal point are not significant.
• Trailing zeroes in a number with decimal place are significant

Cautions to remove ambiguities in determining number of significant figures

• Change of units should not change number of significant digits.

Example: 4.700m = 470.0 cm = 4700 mm. In this, first two quantities have 4 but third quantity has 2 significant figures.

• Use scientific notation to report measurements.
• Numbers should be expressed in powers of 10 like a x 10^b where b is called order of magnitude.

Example : 4.700 m = 4.700 x 10² cm = 4.700 x 10³ mm = 4.700 x 10^-3 In all the above, since power of 10 are irrelevant, number of significant figures are 4.

• Multiplying or dividing exact numbers can have infinite number of significant digits.

Example: radius = diameter / 2. Here 2 can be written as 2, 2.0, 2.00, 2.000 and so on.

• For a number greater than 1, without any decimal, the trailing zero(s) are not significant.
• For a number with a decimal, the trailing zero(s) are significant

---

Rules for Arithmetic operation with Significant Figures

Type	Multiplication or Division	Addition or Subtraction
Rule	The final result should retain as many significant figures as there in the original number with the lowest number of significant digits.	The final result should retain as many decimal places as there in the original number with the least decimal places.
Example	Density = Mass / Volume if mass = 4.237 g (4 significant figures) and Volume = 2.51 cm3 (3 significant figures) Density = 4.237 g/2.51 cm3 = 1.68804 g cm-3 = 1.69 g cm-3 (3 significant figures)	Addition of 436.32 (2 digits after decimal), 227.2 (1 digit after decimal) &  .301 (3 digits after decimal) is = 663.821 Since 227.2 is precise up to only 1 decimal place, Hence, the final result should be 663.8

---

Rules for Rounding off the uncertain digits

Rounding off is necessary to reduce the number of insignificant figures to adhere to the rules of arithmetic operation with significant figures.

Rule Number	Insignificant Digit	Preceding Digit	Example (rounding off to two decimal places)
1	Insignificant digit to be dropped is more than 5	Preceding digit is raised by 1.	Number – 3.137 Result – 3.14
2	Insignificant digit to be dropped is less than 5	Preceding digit is left unchanged.	Number – 3.132 Result – 3.13
3	Insignificant digit to be dropped is equal to 5	If preceding digit is even, it is left unchanged.	Number – 3.125 Result – 3.12
4	Insignificant digit to be dropped is equal to 5	If preceding digit is odd, it is raised by 1.	Number – 3.135 Result – 3.14

---

Rules for Determining the Uncertainty in the Results of Arithmatic Calculations :

To calculate the uncertainty, below process should be used.

• Add a lowest amount of uncertainty in the original numbers.

Example:  uncertainty for 3.2 will be ± 0.1 and for 3.22 will be ± 0.01. Calculate these in percentage also.

• After the calculations, the uncertainties get multiplied/divided/added/subtracted.
• Round off the decimal place in the uncertainty to get the final uncertainty result.

Example: For a rectangle, if length l = 16.2 cm and breadth b = 10.1 cm

Then, take l = 16.2 ± 0.1 cm or 16.2 cm ± 0.6% and breadth = 10.1 ± 0.1 cm or 10.1 cm ± 1%.

On Multiplication, area = length x breadth = 163.62 cm² ± 1.6% or 163.62 ± 2.6 cm².

Therefore after rounding off, area = 164 ± 3 cm².

Hence 3 cm² is the uncertainty or the error in estimation.

Rules:

(i) If a set of experimental data is specified to n significant figures, a result obtained by combining the data will also be valid to n significant figures.

If data are subtracted, the number of significant figures can be reduced.

Example:  12.9 g – 7.06 g = 5.84 g , both 12.9 g & 7.06 g specified to three significant figures, cannot properly be evaluated as 5.84 g but only as 5.8 g, as uncertainties in subtraction or addition combine in a different fashion.

(ii) The relative error of a value of number specified to significant figures depends not only on n but also on the number itself.

Example: accuracy for two numbers 1.02 and 9.89 is ±0.01. But relative errors will be:

For 1.02, (± 0.01/1.02) x 100% = ± 1%

For 9.89, (± 0.01/9.89) x 100% = ± 0.1%

Hence, the relative error depends upon number itself.

(iii) Intermediate results in multi-step computation should be calculated to one more significant figure in every measurement than the number of digits in the least precise measurement.

Example: 1/9.58 = 0.1044

Now, 1/0.104 = 9.56 and 1/0.1044 = 9.58

Hence, taking one extra digit gives more precise results and reduces rounding off errors.

All the physical quantities represented by derived units can be expressed in terms of some combination of seven  fundamental or base quantities.

We shall call these base quantities as the seven dimensions of the physical world, which are denoted with square brackets [ ].

Thus, length has the dimension [L], mass [M], time [T], electric current [A], thermodynamic temperature [K], luminous intensity [cd], and amount of substance [mol].

The dimensions of a physical quantity are the powers (or exponents) to which the base quantities are raised to represent that quantity.

Examples: (i) Volume = Length x Breadth x Height = [L] x [L] x [L] = [L]³ = [L³]

(ii) Force = Mass x Acceleration = = mass × (length)/(time)² = [M][L]/[T]² = [MLT^-2]

• The other dimensions for a quantity are always 0.

Example: For volume only length has 3 dimensions but the mass, time etc have 0 dimensions. Zero dimension is represented by superscript 0 like [M⁰].

Dimensions do not take into account the magnitude of a quantity.

Dimensional Formula is the expression which shows how and which of the base quantities represent the dimensions of a physical quantity.

Therefore  dimensional formula of the volume is [M° L³ T°],

Dimensional formula of the  speed or velocity is [M° L T^-1].

Similarly,  the dimensional formula of acceleration is [M° L T^–2]

Dimensional formula of the mass density.  [M L^–3 T°]

Dimensional equations :  is an equation obtained by equating a physical quantity with its dimensional formula.

Example: The dimensional equations of volume [V], speed [v], force [F ] and mass density [ρ] may be expressed as

[V] = [M⁰ L³ T⁰]
[v] = [M⁰ L T^–1]
[F] = [M L T^–2]
[ρ] = [M L^–3 T⁰]

---

Dimensional Analysis :

• Only those physical quantities which have same dimensions can be added and subtracted. This is called principle of homogeneity of dimensions.
• Dimensions can be multiplied and cancelled like normal algebraic methods.
• In mathematical equations, quantities on both sides must always have same dimensions.
• Arguments of special functions like trigonometric, logarithmic and ratio of similar physical quantities are dimensionless.
• Equations are uncertain to the extent of dimensionless quantities.

Example : Distance = Speed x Time. In Dimension terms, [L] = [LT^-1] x [T]

Since, dimensions can be cancelled like algebra, dimension [T] gets cancelled and the equation becomes [L] = [L].

A thorough understanding of dimensional analysis helps us in deducing certain relations among different physical quantities and checking the derivation, accuracy and dimensional consistency or homogeneity of various mathematical expressions.

---

Applications of Dimensional Analysis :

Checking Dimensional Consistency of equations

• A dimensionally correct equation must have same dimensions on both sides of the equation.
• A dimensionally correct equation need not be a correct equation but a dimensionally incorrect equation is always wrong. It can test dimensional validity but not find exact relationship between the physical quantities.

Example: x = x₀ + v₀t + (1/2) at² Or Dimensionally, [L] = [L] + [LT^-1][T] + [LT^-2][T²]

[L] = [L] + [L] + [L]

x – Distance traveled in time t, x₀ – starting position, v₀ - initial velocity, a – uniform acceleration.

Dimensions on both sides will be [L] as [T] gets cancelled out. Hence this is dimensionally correct equation.

Deducing relation among physical quantities

• To deduce relation among physical quantities, we should know the dependence of one quantity over others (or independent variables) and consider it as product type of dependence.
• Dimensionless constants cannot be obtained using this method.

Example: T = k l^xg^ym^z

Or [L⁰M⁰T¹] = [L¹]^x [L¹T^-2]^y [M¹]^z= [L^x+yT^-2y M^z]

Means, x+y = 0, -2y = 1 and z = 0. So, x = ½, y = -½ and z = 0

So the original equation reduces to T = k\(\sqrt{l\over g}\)

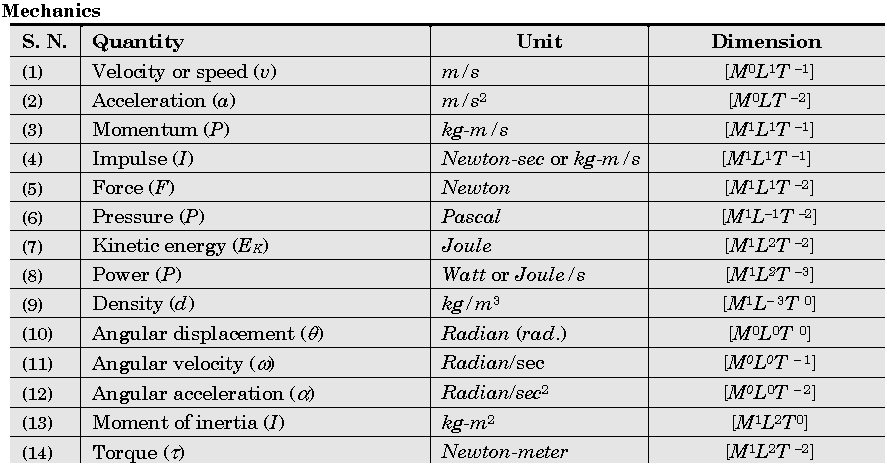
Important Dimensions of Complete Physics:

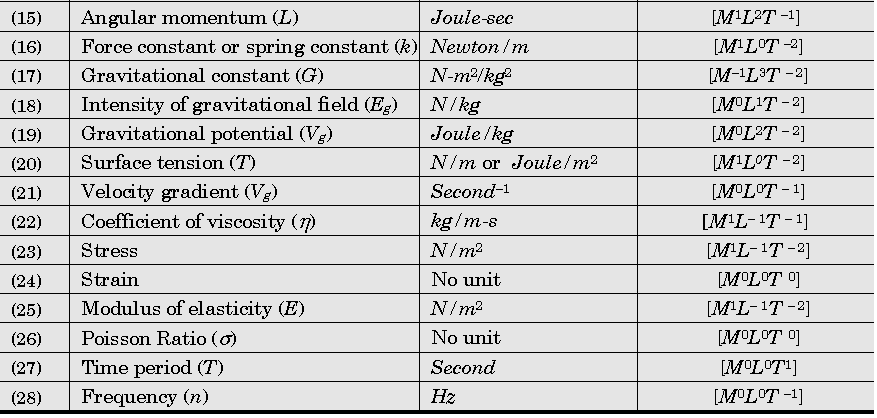
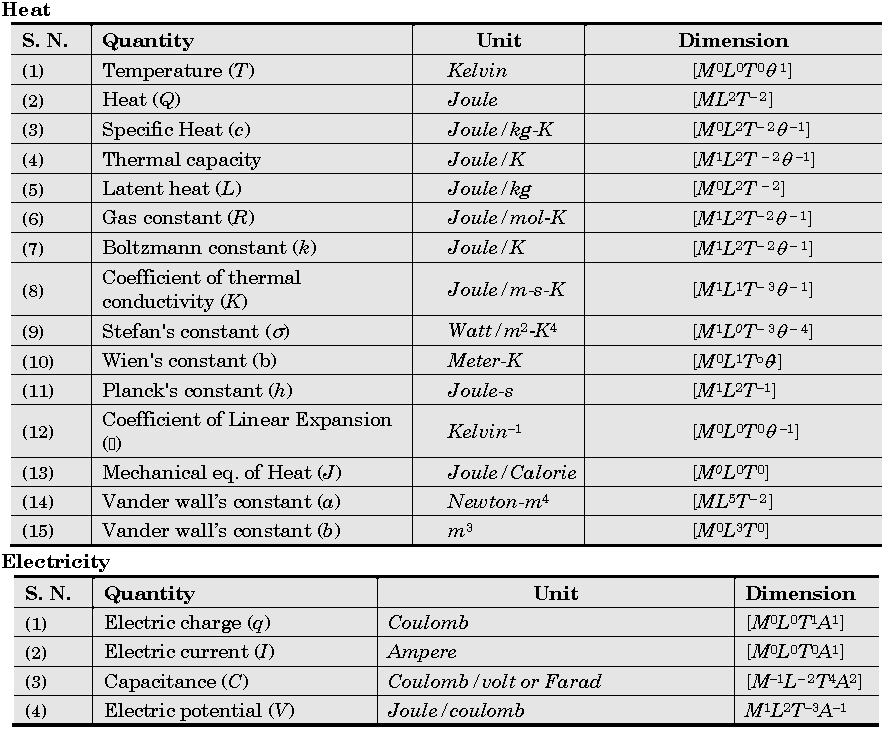
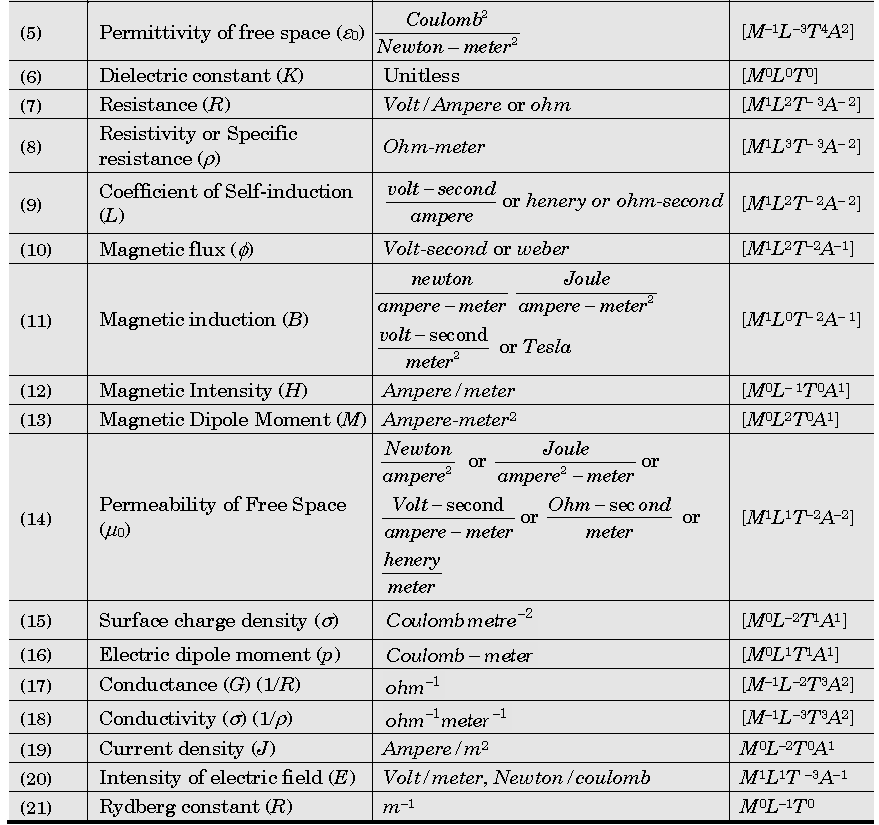
Quantities Having Same Dimensions :

 

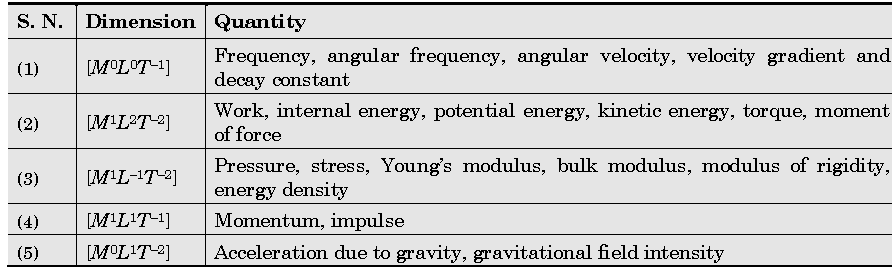
Example:

(i) Let us consider an equation \(\frac{1}{2}\)\( mv^2\) = mgh
where m is the mass of the body, v its velocity, g is the acceleration due to gravity and h is the height.

Check whether this equation is dimensionally correct.

Answer :

The dimensions of LHS are
[M] [L T^–1 ]² = [M] [ L² T^–2] = [M L² T^–2]

The dimensions of RHS are
[M][L T^–2] [L] = [M][L² T^–2] = [M L² T^–2]

The dimensions of LHS and RHS are the same and hence the equation is dimensionally correct.

---

(ii) The SI unit of energy is J = kg m² s^–2; that of speed v is m s^–1 and of acceleration a is m s^–2.

Which of the formulae for kinetic energy (K) given below can you rule out on the basis of dimensional arguments (m stands for the mass of the body) :
(a) K = m² v³
(b) K = (1/2)mv²
(c) K = ma
(d) K = (3/16)mv²
(e) K = (1/2)mv² + ma

Answer :

Every correct formula or equation must have the same dimensions on both sides of the equation.

Also, only quantities with the same physical dimensions can be added or subtracted.

The dimensions of the quantity on the right side are

[M² L³ T^–3] for (a);

[M L² T^–2] for (b) and (d);

[M L T^–2] for (c).

The quantity on the right side of (e) has no proper dimensions since two quantities of different dimensions have been added.

Since the kinetic energy K has the dimensions of [M L² T^–2], formulas (a), (c) and (e) are ruled out.

Note that dimensional arguments cannot tell which of the two, (b) or (d), is the correct formula.

For this, one must turn to the actual definition of kinetic energy (see Chapter 6). The correct formula for kinetic energy is given by (b).

SUMMARY:

1. Physics is a quantitative science, based on measurement of physical quantities. Certain physical quantities have been chosen as fundamental or base quantities (such as length, mass, time, electric current, thermodynamic temperature, amount of substance, and luminous intensity).

2. Each base quantity is defined in terms of a certain basic, arbitrarily chosen but properly standardised reference standard called unit (such as metre, kilogram, second, ampere, kelvin, mole and candela).

The units for the fundamental or base quantities are called fundamental or base units.

3. Other physical quantities, derived from the base quantities, can be expressed as a combination of the base units and are called derived units.

A complete set of units, both fundamental and derived, is called a system of units.

4. The International System of Units (SI) based on seven base units is at present internationally accepted unit system and is widely used throughout the world.

5. The SI units are used in all physical measurements, for both the base quantities and the derived quantities obtained from them.

Certain derived units are expressed by means of SI units with special names (such as joule, newton, watt, etc).

6. The SI units have well defined and internationally accepted unit symbols (such as m for metre, kg for kilogram, s for second, A for ampere, N for newton etc.).

7. Physical measurements are usually expressed for small and large quantities in scientific notation, with powers of 10.

Scientific notation and the prefixes are used to simplify measurement notation and numerical computation, giving indication to the precision of the numbers.

8. Certain general rules and guidelines must be followed for using notations for physical quantities and standard symbols for SI units, some other units and SI prefixes for expressing properly the physical quantities and measurements.

9. In computing any physical quantity, the units for derived quantities involved in the relationship(s) are treated as though they were algebraic quantities till the desired units are obtained.

10. Direct and indirect methods can be used for the measurement of physical quantities. In measured quantities, while expressing the result, the accuracy and precision of measuring instruments along with errors in measurements should be taken into account.

11. In measured and computed quantities proper significant figures only should be retained.
Rules for determining the number of significant figures, carrying out arithmetic operations with them, and ‘rounding off ‘ the uncertain digits must be followed.

12. The dimensions of base quantities and combination of these dimensions describe the nature of physical quantities.

Dimensional analysis can be used to check the dimensional consistency of equations, deducing relations among the physical quantities, etc.

A dimensionally consistent equation need not be actually an exact (correct) equation, but a dimensionally wrong or inconsistent equation must be wrong.