Notes-Part-1
|
PART-1 1) Introduction 2) Fluid, Fluids at rest 3) Pressure
|
Fluid : A fluid is a substance that can flow. A fluid has shear modulus @ 0 and yield to shear. Under a shear stress and a pressure gradient, a fluid begins to flow. Liquids, gases and plasmas are collectively called fluids.
Examples : All gases, all liquids, molten glass and lava, honey, etc.
Properties of Fluids:
Ideal fluid -Characteristics of an ideal fluid. An ideal fluid is one that has the following properties :
Incompressible fluid : An incompressible fluid is one which does not undergo change in volume for a large range of pressures. Thus, its density has a constant value throughout the fluid. In most cases, all liquids are incompressible.
Q. How does a fluid differ from a solid?
2) Within the elastic limit, both types of deformation is reversible. 3) A solid changes its shape under a shear. 4) A normal force causes a change in its length or volume. 5) If the elastic limit is exceeded, the solid gets an irreversible deformation called a permanent set. 2) A fluid does not have a definite shape, so that under a shear it begins to flow. 3) Real fluids, with non-Zero viscosity, display a weak resistance to shear.
Solid
Fluid
1) In response to a shear as well as normal force, a solid deforms and develops a restoring force.
1) A fluid, on the other hand, can only be subjected to normal compressive stress, called pressure.
Plasma : Plasma is a phase of matter which exists at very high temperatures, at which molecules may disassociate into atoms and ions, and further into electrons and protons. Plasma, however, has very different properties from the three other common phases of matter (viz., solid, liquid and gas) due to the strong electrical forces between the charges.
| The term fluid includes both the liquid and gas phases.
It is commonly used, as a synonym for liquid only, without any reference to gas. For example, ’brake fluid’ is hydraulic oil and will not perform its required function if there is gas in it! This colloquial use of the term is also common in the fields of medicine and nutrition, e.g. ”take plenty of fluids.” |
Pressure
Pressure : The pressure at a point in a fluid in hydrostatic equilibrium is defined as the normal force per unit area exerted by the fluid on a surface of infinitesimal area containing the point.
Thus, the pressure, \(p= \lim\limits_{ΔA\to 0} \frac{F}{ΔA}\)
where F is the magnitude of the normal force on a surface of area ΔA. The pressure is defined to be a scalar quantity.
SI unit = the pascal (Pa), 1 Pa = 1 N-m-2
CGS unit : the dyne per square centimeter (dyn/cm2)
Dimensions = [p] = [F][A-1] = [MLT-2, L-2 ] = [ML-1T-2]
Two non-SI units of pressure, which are either of historical interest, or are still used in specific fields are the bar and the torr.
1 bar = 0.1 MPa = 100 kPa = 1000 hPa =105Pa
1 torr = (101325/ 760) Pa = 133.32 Pa
[Note : Their use in modern scientific and technical work is strongly discouraged]
Q. Explain why the forces acting on any surface within a fluid in hydrostatic equilibrium must be normal to the surface.
Ans. In a fluid, the molecules are in a state of random motion and the intermolecular cohesive forces are weak. If a fluid is subjected to a tangential force (shear) anywhere within it, the layers of the fluid slide over one another, i.e., the fluid begins to flow. Within in a static fluid, forces on a volume element are normal to the surface Thus, a fluid cannot sustain a tangential force. So, in turn, a fluid at rest cannot exert a tangential force on any surface with which it is in contact. It can exert only a force normal to the surface. Hence, if a fluid is in In hydrostatic equilibrium (i.e., at rest), the force acting on any surface within the fluid must be normal to the surface.
Q. Why does a knife have a sharp edge or a needle has a sharp tip ?
For a given force, the pressure over which the force is exerted depends inversely on the area of contact; smaller the area, greater the pressure. For instance, A pressure for a force applied to an area of 1 mm2 is 100 times as great as than pressure for the same force applied to an area of 1 cm2. The edge of a knife or the tip of a needle has a small area of contact. That is why a sharp needle is able to puncture the skin when a small force is exerted, but applying the same force with a finger does not.
Expression for pressure exerted by a liquid column. At a point at depth h below the surface of a liquid of uniform density r, the pressure due to the liquid is due to the weight per unit area of a liquid column of height h above that point. In Fig. to find the pressure due to the liquid at point P, consider the cylindrical liquid column, of cross section A and height h, above that point. The weight of this liquid column = volume X density X acceleration due to gravity = (Ah)(ρ)(g) Pressure due to the liquid at depth h = weight of the liquid column / cross sectional area Ahρg/A = hρg If the free surface of the liquid is open to the atmosphere, the pressure on the surface is the atmosphere pressure P0. Then, the absolute pressure within the liquid at a depth h is P = P0+ hρg 2. p = hρg is true for liquids as well as for gases.
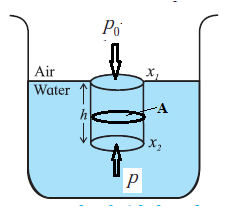
1. As p = hρg , the pressure exerted by a fluid at rest is independent of the shape and size of the container.
Characteristics of pressure due to a liquid at rest at a point within it :
Atmospheric pressure : The Earth's surface is covered with a layer of atmosphere, with more than 99% of the atmosphere lying within 31 km of the surface. The weight of the atmosphere exerts a downward thrust on any surface lying within it. This gives rise to atmospheric pressure.
The atmospheric pressure at any height above the Earth's surface is the weight of a column of air of unit cross section from that altitude to the top of the atmosphere.
Standard atmospheric pressure : Standard atmospheric pressure, or one atmosphere of pressure, is defined as the pressure equivalent of a column of mercury that is exactly 0.7600 m in height at 0 °C. We can calculate this equivalent pressure in SI unit by using the density of mercury ρ = 13.6 X103 kg/m3 and g =9.80 m/s2. 1 atm = (0.76 m)(13.6 X 103 kg/m3)(9.80 m/s2) = 1.013 X105 Pa = 101.3 kPa [Note : 1000 mbar = 100 kPa. Therefore, 1 atm = 1013 mbar.]
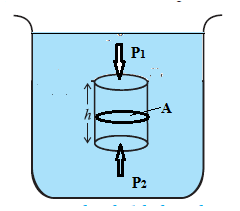
Q. Explain gauge pressure and absolute pressure within a liquid open to the atmosphere. QR Explain the effect of gravity on fluid pressure.
Consider a cylindrical fluid column of uniform density r, area of cross section A and height h, Fig. The mass of the fluid within the column is m = density X volume = ρAh If P1 and P2 are the pressures at the top and bottom faces of the column, the forces on the top and bottom faces are respectively. F1 = P1A + mg (downward) and F2 = P2A (upward) If the column is in equilibrium, F2 = F1 P2A = P1A + mg = P1A + ρAhg P2 - P1 = ρhg If P1 = P0 = atmospheric pressure, the gauge pressure P2 - P0 = ρhg In the absence of gravity, P2 = P0. But since atmospheric pressure is equal to the weight per unit area of the entire air column above, even P0 will be zero in the absence of gravity.
Gauge pressure. : Gauge pressure is exerted by a fluid relative to the local atmospheric pressure. Gauge pressure, pg = p- p0 where p is the absolute pressure and p0, is the local atmospheric pressure. Gauge pressure (i) positive (ii) negative : When the pressure inside a closed container or tank is greater than atmospheric pressure, the pressure reading on a pressure gauge is positive. The pressure inside a ‘vacuum chamber' rigid chamber from which some of the air is pumped out—is less than the atmospheric pressure, so a pressure gauge on the chamber designed to measure negative pressure reads a negative value. At a depth within a liquid of density r, the gauge pressure is pg = p- p0 = hρg Examples : Tyre pressure gauge, blond pressure gauge, pressure gauge on an oxygen or scuba tank.
Absolute pressure : The absolute pressure, or total pressure, is measured relative to absolute zero on the pressure scale—which is a perfect vacuum—and is the sum of gauge pressure and atmospheric pressure. It is the same as the thermodynamic pressure. Absolute pressure accounts for the atmospheric pressure, which in effect adds to the pressure in any fluid which is not enclosed in a rigid container i.e., the fluid is open to the atmosphere. p = p0 + pg where p0 and pg are respectively atmospheric pressure and the gauge pressure. Absolute pressure can be never negative.
Hydrostatic paradox : The normal force exerted by a liquid at rest on the bottom of the containing vessel is independent of the amount of liquid or the shape of the container, but depends only on the area of the base and its depth from the liquid surface.
Consider several vessels of the same base area as shown in Fig.
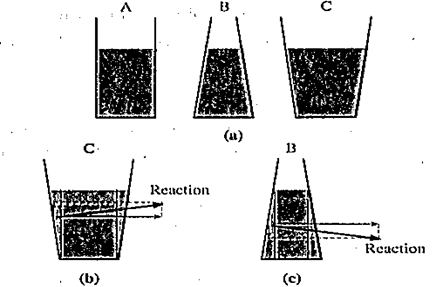
A liquid is poured into them to the same level, so that the pressure is the same at the bottom of each vessel. Then it must follow that the normal force on the base of each vessel is also the same. However, when placed on n scale balance they are found to have different weights. Herein lies the paradox.
Explanation : Since a liquid always exerts a normal force on a wall of the container, in turn, the wall exerts an equal and opposite reaction on the liquid. ln the case of tube A, this reaction is everywhere horizontal; so that the normal force at the base of A is only due to the weight of the liquid column above. The reaction of the slanted wall of vessel C has a vertical component, as shown in Fig. (b), which supports the weight of the liquid above the slanted side. Hence, the normal force at the base of C is only due to the weight of the vertical liquid column above the base, shown by dashed lines. Since the vessels A and C are filled to the same height and have the same base area, the pressures at the bases of the two vessels are also same. However, the volume of the liquid being clearly different, they have different weights. In the case of vessel B, the downward vertical component of the reaction of the wall provides an extra normal force at the base as shown in Fig.(c)
Pascal’s Law:
Pascal’s law states that the pressure applied at any point of an enclosed fluid at rest is transmitted equally and undiminished to every point of the fluid and also on the walls of the container, provided the effect of gravity is neglected.
Note ; The law does not say that ‘the pressure is the same at all points of a fluid’ — rightly so, since the pressure in a fluid near Earth varies with height. Rather, the law applies to the change in pressure. According to Pascal's law, if the pressure on an enclosed static fluid is changedby a certain amount, the pressure at all points within the fluid changes by the same amount.
The above law is due to Blaise Pascal (1623 -62), French mathematician and physicist.]
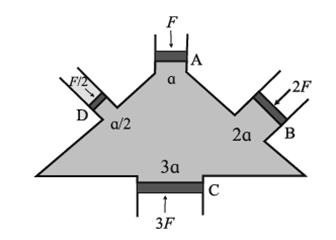
Experimental proof of Pascal’s principle. Consider a vessel with four arms A, B, C, and D fitted with frictionless, water tight pistons and filled with incompressible fluid as shown in the figure given. Let the area of cross sections of A, B, C, and D be a, 2a, 3a, and a/2 respectively. If a force F is applied on the piston A, the pressure exerted on the liquid is p = F/a. It is observed that the other three pistons B, C, and D move outward. In order to keep these three pistons B, C, and D in their original positions, forces 2F, 3F, and F/2 respectively are required to be applied on the pistons. Therefore, pressure on the pistons B, C, and D is: on B, pB = 2F/2a = F/a on C, pC = 3F/3a = F/a and on D, pD = (F/2)/(a/2) = F/a i.e. pB = pC = pD = p, this indicates that the pressure applied on piston A is transmitted equally and undiminished to all parts of the fluid and the walls of the vessel.
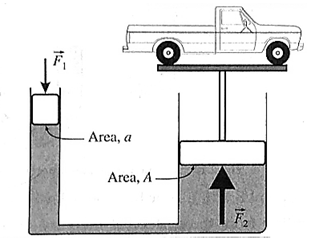
Principle of multiplication of thrust by transmission of fluid pressure : The normal force exerted by a fluid on any surface in contact with it is called the thrust. Consider two hydraulically connected cylinders, one of cross section n and the other A, as in above Fig. If a force Fa is exerted on the smaller piston, pressure p= Fa/a is produced and transmitted undiminished throughout the liquid. Then, the thrust FA on the larger piston is FA = pA = (A/a)Fa If A = na, FA = nFa, i.e., the thrust on the larger piston is multiplied n times. This is known as the principle of multiplication of thrust by transmission of fluid pressure.
Applications of Pascal's law :
(1) Hydraulic car lift and hydraulic press
(2) Hydraulic brakes.
All the above applications work on the principle of multiplication of thrust by transmission of fluid pressure.
(i) Working hydraulic lift : Two hydraulically connected cylinders, one of cross section a and the other A, are such that A is many times larger than a A=na If a force Fa, is exerted on the smaller piston, a pressure p =Fa/a is produced and transmitted undiminished throughout the liquid. Then, the thrust FA on the larger piston FA = pA = (A/a)Fa =n Fa is n times greater than that on the smaller piston. A platform attached to the larger piston can lift a car (as in a hydraulic car lift).
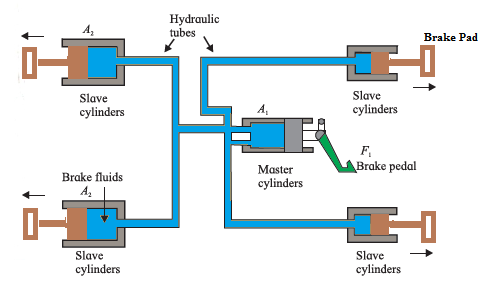
ii) Hydraulic brakes: Hydraulic brakes are used to slow down or stop vehicles in motion. It is based on the same principle as that of a hydraulic lift. Figure shows schematic diagram of a hydraulic brake system. The master cylinder has a smaller area of cross section A1 compared to the area A2 of the slave cylinder. By applying a small force F1 to the master cylinder, we generate pressure p = (F1/A1). This pressure is transmitted undiminished throughout the system. The force F2 on slave cylinder is then, F2 = pA2 = (F1/A1). A2 = F1 (A2/A1) = n F1 (i.e. force is n times greater than that on the smaller piston) This is similar to the principle used in hydraulic lift. Since area A2 is greater than A1, F2 is also greater than F1. Thus, a small force applied on the brake pedal gets converted into large force and slows down or stops a moving vehicle. Advantages of hydraulic brakes :
| (1) Pascal's law laid the foundation for hydraulics, the use of a liquid under pressure to transfer force or motion, or to increase an applied force. It is one of the most important branches in modem engineering.
(2) A hydraulic system, as an example of a simple machine, can increase force but cannot do more work than is done on it. Work being force times the distance moved, the piston in a wheel cylinder moves through a smaller distance than that in the pedal cylinder. Power brakes in modern automobiles have a motorized pump that does most of the work in the system. |
Q. Why are liquids used in hydraulic systems but not gases?
Liquids are used in a hydraulic system because liquids are incompressible and transmit a change in pressure undiminished to all parts of the system. On the other hand, on increasing the pressure, a gas will be compressed into a smaller volume due to which there will be no transmission of force or motion.
i) Mercury Barometer: An instrument that measures atmospheric pressure is called a barometer.
Mercury Barometer was invented by Italian scientist Torricelli. The barometer is in the form of a glass tube completely filled with mercury and placed upside down in a small dish containing mercury. It’s schematic diagram is shown in Fig.
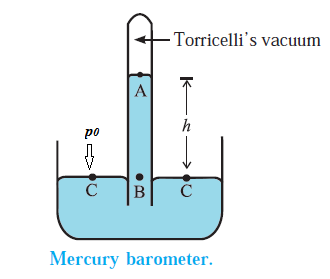
- A strong glass tube, about one metre long and closed at one end, is filled with mercury.
- With a finger over the open end, the tube is inverted and the open end is immersed into a bowl of mercury.
- When the finger is removed, the mercury level in the tube drops.
- The mercury column in the tube stands at a height h for which the pressure at point B inside the tube due to the weight of the mercury column is equal to the atmospheric pressure p0 outside (at point C).
- The space at the closed end of the tube, after the mercury level drops, is nearly a vacuum, known as the Torricellian vacuum, so the pressure there can be taken as zero. It, therefore, follows that p0 = ρgh
- Where r is the density of mercury and h is the height of the mercury column.
Open tube manometer : An open tube manometer is a device to measure the pressure of a gas in a vessel. It consists of a U-shaped tube containing a liquid (say, mercury) of density ρ, as shown in Fig. One end of the tube is connected to the vessel while the other end is open to the atmosphere. The pressure p at point A is the (unknown) pressure of the gas in the vessel. The pressure on the mercury column in the open tube is the atmospheric pressure p0. A point B, at the same horizontal level as A, is at a depth h from the surface of mercury in the open tube. Therefore, the pressure at B is p0 + ρgh. The pressures at points A and B at the same liquid level being the same, equating the unknown pressure p (at A) to the pressure at B. p = p0 + ρgh The pressure p is called the absolute pressure, and the difference in pressure p - p0 is called the gauge pressure.
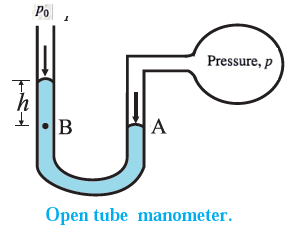
Q. Why is a low density liquid used as a manometric liquid in a physics laboratory?
An open tube manometer measures the gauge pressure, p — p0 = hρg, where p is the pressure being measured, po is the atmospheric pressure, h is the difference in height between the manometric liquid of density ρ in the two arms. For a given pressure P, the product hr is constant. That is, ρ should be small for h to be large. Therefore, for noticeably large h, laboratory manometer uses a low density liquid.
| Next Part >> |
Thanks you.
For a notes
Thank you so much
Thank you so much
Thanks for notes.
Thanks for the notes
THANK U SO MUCH FOR THE NOTES
thanks lol
Thanks you so much it really help ful to use and study physics we save pure time withe use this notes .