Mechanical Properties of Fluid
Class-12th-Physics-Chapter-2-Maharashtra Board
Notes Part-1
|
Topics to be Learn : Part-1
|
Equation of state : The state of a gas is specified by a number of physical quantities such as pressure P, thermodynamic temperature T, volume V, internal energy E, etc. The equation that relates these quantities is known as the equation of state.
The volume V of a gas is inversely proportional to the pressure P, temperature being held constant. Separately, volume V and pressure P are directly proportional to temperature.
- Boyle's law: V ∝ 1/P at constant T
- Charles' law V ∝ T at constant P
- Gay-Lussac's law: P ∝ T at constant V
All the three laws apply to fixed mass m of an enclosed gas.
Ideal or perfect gas : An ideal or perfect gas is a gas which obeys the gas laws (Boyle's law, Charles’ law and Gay—Lussac’s law) at all pressures and temperatures. An ideal gas cannot be liquefied by application of pressure or lowering the temperature.
A molecule of an ideal gas is an ideal particle having only mass and velocity. Its structure and size are ignored. Also, intermolecular forces are zero except during collisions.
Equation of state for an ideal gas : Let P1, V1 and T1 be the pressure, volume and absolute temperature (thermodynamic temperature) of n moles of a gas (assumed to be ideal). Suppose the gas is heated at constant pressure (P1) so that its temperature becomes T and volume becomes V2. Then by Charles’ law, \(\frac{V_2}{V_1}=\frac{T}{T_1}\) …….. (1) ∴ \(T=\frac{V_2T_1}{V_1}\) Now, suppose that the gas is heated at constant volume (V2) so that its temperature becomes T2 and pressure becomes P2. Then by Gay—Lussac’s law, \(\frac{P_2}{P_1}=\frac{T_2}{T}\) ∴ \(T=\frac{P_1T_2}{P_2}\)…….. (2) From equations (1) and (2), we get, \(\frac{V_2T_1}{V_1}=\frac{P_1T_2}{P_2}\) ∴ \(\frac{P_2V_2}{T_2}=\frac{P_1V_1}{T_1}\) When pressure and temperature are constant, V ∝ n. Hence, in general, we can write \(\frac{PV}{T}=nR\) , where R is a proportionality constant, called the universal gas constant. Thus, PV = nRT for an ideal gas. This is the equation of state for an ideal gas. [Note : By Boyle's law, for a fixed mass of gas at constant temperature, V=constant. Writing PV ∝ nT, we get PV = nRT] (i) Ideal gas equation in terms of the Avogadro number In the usual notation, PV= nRT; Now, the number of moles, n = mass of the gas (M) /molar mass (M0) = N/NA (Molar mass is the mass of 1 mole of gas) where N is the number of molecules corresponding to n moles of the gas and NA is the Avogadro number. ∴ PV = \(\frac{N}{N_A}RT\) (ii) Ideal gas equation in terms of the Boltzmann constant : PV = \(\frac{N}{N_A}RT\) = N\(\frac{R}{N_A}T\) = NkBT, where kB = \(\frac{R}{N_A}\) is the Boltzmann constant. . Ideal gas equation in terms of the density of the gas : In the usual notation, PV= nRT; The number of moles, n = mass of the gas (M) /molar mass (M0) ∴ PV = \(\frac{M}{M_0}RT\) ∴ P = \(\frac{M/V}{M_0}RT\) = \(\frac{ρ}{M_0}RT\) , where ρ =M/V is the density of the gas.
The basic assumptions of the kinetic theory of an ideal gas :
Distinguish between an ideal gas and a real gas : Under these conditions, the density of a gas is very low. Hence, the molecules, on an average, are far away from each other. The intermolecular forces are then not of much consequence
Ideal gas
Real gas
Molecules of an ideal gas behave as ideal particles, i.e., they are like geometrical points without size and structure.
Molecules of a real gas have finite size and structure.
Molecules of an ideal gas have only translational motion.
Polyatomic molecules have in general, translational, vibrational and rotational motion.
There are no intermolecular forces in this case.
Intermolecular forces are non-zero in this case.
An ideal gas cannot be liquefied.
A real gas can be liquefied and also solidified in many cases, by application of pressure and reducing temperature.
There are no intermolecular collisions in this case.
There are intermolecular collisions in this case, and under normal conditions the collision frequency is very high.
In the absence of intermolecular forces, the internal energy of the gas is only kinetic.
Due to the intermolecular forces, the internal energy of the gas is (potential energy + kinetic energy.)
A real gas obeys ideal gas equation when temperature is very high and pressure is very low.
| 1. At high pressure and low temperature, intermolecular forces become very important as the average separation between two molecules is very less compared to that at low pressure and high temperature. Therefore at high pressure and low temperature deviation of a real gas from ideal gas behaviour is observed.
2. Phenomena of diffusion, viscosity and thermal conductivity depend upon the average distance covered by a molecule between successive collisions and hence on the size of the molecules. The greater the molecular diameter, the less is (i) the coefficient of viscosity (ii) the thermal conductivity of a real gas. 3. An ideal gas does not exist in reality. |
Mean free path
Concept of free path of a gas molecule : Molecules of a real gas are not point like particles. For simplicity, molecules are assumed to be spherical. Because of their finite size, two molecules collide with each other when they come within a molecular diameter of each other, strictly speaking, within the sphere of influence of each molecule. The molecular collisions, though perfectly elastic, result in significant changes in the speeds and directions of motion of the molecules. Hence, every molecule follows a zigzag path, with abrupt changes in its speed and direction of motion at short and random time intervals. This is called Brownian motion (see Fig.).
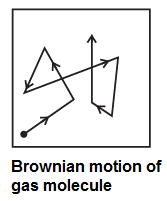
Free path : The straight line path of a molecule, i.e., the distance covered by it between successive collisions, is called a free path.
Mean free path : The average distance travelled by a gas molecule between successive collisions, the average being taken over a large number of free paths (or collisions) is called the mean free path.
Expression for mean free path : Maxwell, on the basis of the law of distribution of molecular speeds, obtained the formula for the mean free path (λ) as λ = \(\frac{1}{\sqrt{2}πd^2\frac{N}{V}}\) where N is the number of molecules in volume V of the gas and d is the diameter of a molecule. Expression for the mean free path of a gas molecule in terms of pressure and temperature : In the usual notation, the mean free path of a gas molecule, λ = \(\frac{1}{\sqrt{2}πd^2\frac{N}{V}}\) Now PV=nRT PV = \(\frac{N}{N_A}\)RT = N\(\frac{R}{N_A}\)T = NkBT ∴ \(\frac{N}{V}\) = \(\frac{P}{k_BT}\) ∴ λ = \(\frac{1}{\sqrt{2}πd^2P}\) Expression for the mean free path of a gas molecule in terms of the density of the gas : In the usual notation, the mean free path of a gas molecule, λ = \(\frac{1}{\sqrt{2}πd^2\frac{N}{V}}\) Density, ρ of the gas = mass/volume = mN/V , where m is the molecular mass. ∴ N/V = ρ/m ∴ λ = \(\frac{m}{\sqrt{2}πd^2ρ}\)
Factors on which the mean free path of a gas molecule depends :
The mean free path of a gas molecule depends upon the number of molecules per unit volume of the gas and molecular diameter.
If there is
- Increase in temperature at constant pressure, the mean free Path of a gas molecule increases.
- Increase in pressure at constant temperature, the mean free Path of a gas molecule decreases.
| If the pressure of a gas in an enclosure is reduced by evacuating it, the density of the gas decreases and the mean free path increases.
You must have seen articles coated with metal films. The metals are heated and evaporated in an enclosure. The pressure in the enclosure is reduced so that the mean free path of air molecules is larger than the dimensions of the enclosure. The atoms in the metal vapour then do not collide with the air molecules. They reach the target and get deposited. |
Pressure of an ideal gas - Root mean square (rms) speed - Interpretation of temperature in kinetic theory
Origin of pressure exerted by a gas on the walls of a container :
The pressure exerted by a gas on the walls of a container results from the momentum transfer during the collisions of the gas molecules with the walls. The normal force on a wall by all the molecules, per unit wall area, is the gas pressure on the wall.
Mean (or average) speed of molecules of a gas :The mean speed of gas molecules is defined as the arithmetic mean of the speeds of all molecules of the gas at a given temperature.
Mean square speed of molecules of a gas :The mean square speed of gas molecules is defined as the arithmetic mean of the squares of the speeds of all molecules of the gas at a given temperature.
Root-mean-square speed of molecules of a gas :The root-mean-square (rms) speed of gas molecules is defined as the square root of the arithmetic mean of the squares of the speeds of all molecules of the gas at a given temperature.
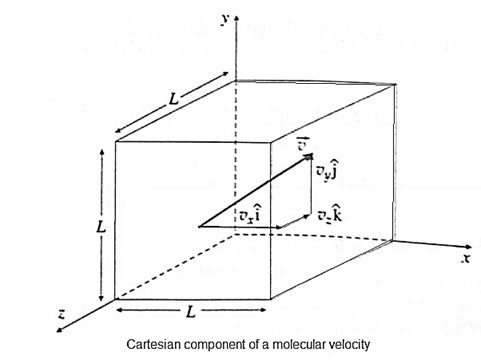
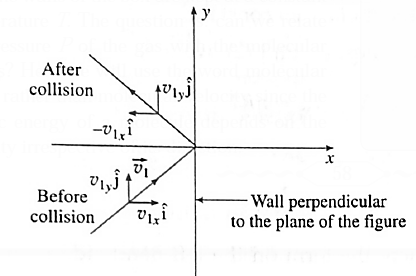
Expressions : If there are N molecules in an enclosed pure gas and v1, v2, v3, ..., vN are the speeds of different molecules, (i) the mean speed, v = \(\frac{v_1+v_2+.....v_N}{N}\) (ii) the mean square speed, \(\vec{v^2}=\frac{v_1^2+v_2^2+.....v_N^2}{N}\) (iii) the rms speed, vrms = \(\sqrt{v^2}\) The mean square velocity is numerically equal to the mean square speed. Similarly, the rms velocity is numerically equal to the rms speed. But in random motion, the mean velocity would be statistically zero, but the mean speed cannot be zero. On the basis of the kinetic theory of gases, derive an expression for the pressure exerted by the gas. The pressure exerted by a gas on the walls of a container results from the momentum transfer during the collisions of the gas molecules with the walls. The normal force on the wall by all the molecules, per unit wall area, is the gas pressure on the wall. Consider a very dilute gas at a steady state temperature enclosed in a cubical container of Side L The coordinate axes are aligned with the edges of this cube, as shown in above Fig. Suppose that there are molecules in the container, each of mass m. Consider a molecule moving with velocity \(\vec{v_1}\) \(\vec{v_1}=v_{1x}i+v_{1y}j+v_{1z}k\) ………. (1) Where v1x, v1y, and v1z are the velocity components along the x—, y- and z—axes, respectively, so that \(v_1^2=v_{1x}^2+v_{1y}^2+v_{1z}^2\) The change in momentum of the molecule on collision with the right wall = final momentum — initial momentum = (-m| v1x |) - m|v1x| = - 2m|v1x| Assuming the collision to be elastic, the change in momentum of the right wall clue to this collision is 2m |v1x|. Since the distance between the right and left walls is L, the time between successive collisions with the right wall is, Δt = \(\frac{2L}{|v_1x|}\) Therefore, the frequency with which the molecule collides with the right wall is \(\frac{|v_1x|}{2L}\) ∴ Rate of change of momentum of the right wall = (change in momentum in one collision)-(frequency of collision) = (2m |v1x|) \(-\frac{|v_1x|}{2L}\) = \(\frac{mv_1^2x}{L}\)……… (2) By Newton's second law of motion, this is the force fix exerted by the molecule on the right wall. Thus, the net force on the right wall by all the N molecules is Fx = f1x +f2x+….+fNx = \(\frac{mv_{1x}^2}{L}+\frac{mv_{2x}^2}{L}+......\frac{mv_{Nx}^2}{L}\) = \(\frac{m}{L}(v_{1x}^2x+v_{2x}^2+......v_{Nx}^2)\) ……. (3) The pressure Px exerted by all the molecules on a wall perpendicular to the x-axis is Px = \(\frac{F_x}{L^2}=\frac{m}{L^3}(v_{1x}^2+v_{2x}^2+......v_{Nx}^2)\) = \(\frac{m}{V}(v_{1x}^2+v_{2x}^2+......v_{Nx}^2)\)………….(4) Where V = L3 is the volume of the container. Similarly, Py = \(\frac{m}{V}(v_{1y}^2+v_{2y}^2+......v_{Ny}^2)\) ………(5) and Pz = \(\frac{m}{V}(v_{1z}^2+v_{2z}^2+......v_{Nz}^2)\) ………..(6) As pressure is the same in all directions, Px = Py = Pz = P (say) ∴ Px + Py + Pz = 3P ……….(7) P = \(\frac{1}{3}\)( Px + Py + Pz ) = \(\frac{m}{3V}[(v_{1x}^2+v_{2x}^2+......v_{Nx}^2)+(v_{1y}^2+v_{2y}^2+......v_{Ny}^2)+.....(v_{1z}^2+v_{2z}^2+......v_{Nz}^2)]\) = \(\frac{m}{3V}[(v_{1x}^2+v_{1y}^2+......v_{1zx}^2)+(v_{2x}^2+v_{2y}^2+......v_{2z}^2)+.....(v_{Nx}^2+v_{Ny}^2+......v_{Nz}^2)]\) = \(\frac{m}{3V}(v_1^2+v_2^2+....v_N^2)\) ……. (8) By definition, the mean square speed of the gas molecules is \(\bar{v^2}=\frac{v_1^2+v_2^2+....v_N^2}{N}\) ∴ \(v_1^2+v_2^2+....v_N^2\) = \(N\bar{v^2}\) ….……. (9) ∴ P = \(\frac{1Nm}{3V}\vec{v^2}\) Here, Nm = (number of molecules)x(molecular mass) = mass of the gas, M ∴ \(\frac{Nm}{V}\) = \(\frac{M}{V}\)= density ρ ∴ P = \(\frac{1}{3}ρ\bar{v^2}\) ….. (11) Writing \(\bar{v^2}\) = \(v_{rms}^2\) ∴ P = \(\frac{1}{3}ρv_{rms}^2\) ….. (12) where vrms is the root-mean-square speed of molecules of the at a given temperature. Equation, P = \(\frac{1}{3}ρv_{rms}^2\) gives the pressure exerted by an ideal gas in terms of its density and the root—mean-square speed of its molecules.
Q. Assuming the expression for the pressure P exerted by an ideal gas, prove that the kinetic energy per unit volume of the gas is P.
According to the kinetic theory of gases, the pressure P exerted by the gas is P = \(\frac{1}{3}ρv_{rms}^2\) = \(\frac{1}{3}\frac{M}{V}v_{rms}^2\) ∴ PV = \(\frac{2}{3}(\frac{1}{2}Mv_{rms}^2)\) Here, \(\frac{1}{2}\frac{M}{V}v_{rms}^2\) is the total kinetic energy (KE) of all molecules of the gas. ∴ PV = \(\frac{2}{3}\)(KE) ∴ KE = \(\frac{3}{2}\)(PV) ∴ \(\frac{KE}{V}=\frac{3}{2}\)(P)\) Thus, the kinetic energy per unit volume of an ideal gas is \(\frac{3}{2}\)(P)\)
Q. Show that the rms velocity of gas molecules is directly proportional to the square root of its absolute temperature.
According to the kinetic theory of gases, the pressure P exerted by a gas is P = \(\frac{1}{3}ρv_{rms}^2\) = \(\frac{1}{3}\frac{M}{V}v_{rms}^2\) ∴ PV = \(\frac{1}{3}Mv_{rms}^2\) where vrms is the rms speed (root-rnean-square speed) of the gas molecules, M, V, and r are the mass, volume and density of the gas, respectively. If there are n moles of the gas and M0 is the molar mass M= nM0 so that PV = \(\frac{1}{3}nM_0v_{rms}^2\) …… (1) The equation of state of an ideal gas is PV = nRT …… (2) Where T is the absolute temperature of the gas and R is the molar gas constant. From Eqs. (1) and (2), we get \(\frac{1}{3}nM_0v_{rms}^2\) = nRT \(M_0v_{rms}^2)\)= 3RT …… (3) \(\frac{1}{2}nM_0v_{rms}^2\) = \(\frac{3}{2}\)RT ……. (4) where the term on the left hand side is the kinetic energy of one mole of the gas. Kinetic energy per mole of the gas = \(\frac{3}{2}\)RT ... (5) From Eq. (3), \(v_{rms}^2\)= \(\frac{3RT}{M_0}\) \(v_{rms}\)= \(\sqrt{\frac{3RT}{M_0}}\)………..(6) In Eq. (6), R and M0 are constant so that vrms ∝ \(\sqrt{T}\) Thus the rms speed of a gas molecule is directly proportional to the square root of the absolute temperature of the gas.
Expression for the kinetic energy per unit mass of the gas :
Refer Eq. (5) from above
Kinetic energy per mole of the gas = \(\frac{3}{2}\)RT
∴ Kinetic energy per unit mass of the gas = \(\frac{\text{KE per mole}}{\text{molar mass}}\)
= \(\frac{3}{2M_0}\)RT
Q. Prove that the kinetic energy per molecule of an ideal gas is kBT.
Consider n moles of an ideal gas in a container of volume V. If m is the mass of a gas molecule and vrms is the root-mean-square speed of the gas molecules then, by the kinetic theory, the pressure exerted by the gas is P = \(\frac{1}{3}\frac{Nm}{V}v_{rms}^2\) ……. (1) where N is the number of molecules of the gas; N = nNA, where NA is the Avogadro number. PV = \(\frac{1}{3}Nmv_{rms}^2\) = \(\frac{2}{3}N(\frac{1}{2}mv_{rms}^2)\)…………….(2) The equation of state of an ideal gas is PV = nRT …(3) ∴\(\frac{2}{3}N(\frac{1}{2}mv_{rms}^2)\) = nRT \(\frac{1}{2}mv_{rms}^2\) = \(\frac{3n}{2N}RT\) = \(\frac{3}{2}\frac{N/N_A}{N}RT\) = \(\frac{3}{2}\frac{R}{N_A}T\) .... ... (4) The left-hand side is the kinetic energy per molecule and R/NA = kB the Boltzmann constant. ∴ KE per molecule = \(\frac{3}{2}k_BT\) ……..(5) Therefore, the kinetic energy per molecule of an ideal gas is directly proportional to its absolute temperature. This equation is the relation between the kinetic per molecule of a gas and the absolute temperature which is the macroscopic parameter of the gas. The absolute temperature of a gas is a measure of the kinetic energy per molecule of the gas. This result is called the kinetic interpretation of temperature, i.e., the interpretation of temperature according to the kinetic theory of gases. Also from eq. (5) \(\frac{1}{2}mv_{rms}^2\) = \(\frac{3}{2}k_BT\) ∴\(v_{rms}=\sqrt{\frac{3k_BT}{m}}\) this proves that the rms speed of the molecules of an ideal gas at an absolute temperature T is \(\sqrt{\frac{3k_BT}{m}}\)
Boyle's law : At a constant temperature, the pressure exerted by a fixed mass of gas is inversely proportional to its volume. If P and V denote the pressure and volume of a fixed mass of gas, then, PV = constant at a constant temperature, for a fixed mass of gas.
Deduce Boyle's law using the expression for pressure exerted by an ideal gas : According to the kinetic theory of gases, the pressure exerted by the gas is P = \(\frac{1}{3}\frac{Nm}{V}v_{rms}^2\) where N is the number of molecules of the gas, m is the mass of a single molecule, vrms is the rms speed of the molecules and V is the volume occupied by the gas. PV = \(\frac{2}{3}N(\frac{1}{2}mv_{rms}^2)\) = (KE of a gas molecule)x\(\frac{2}{3}N\) ……..(1) For a fixed mass of gas, N is constant. Further, inter-molecular forces are ignored so that the corresponding potential energy of the gas molecules may be assumed to be zero. Therefore, \(\frac{1}{2}mv_{rms}^2\) is the total energy of a gas molecule and N\(\frac{1}{2}mv_{rms}^2\) is the total energy of the gas molecules, which is proportional to the absolute temperature of the gas. Then, the right—hand side of Eq. (1) will be constant if its temperature is constant. Hence, it follows that PV = constant for a fixed mass of gas at constant temperature, which is Boyle's law.
|
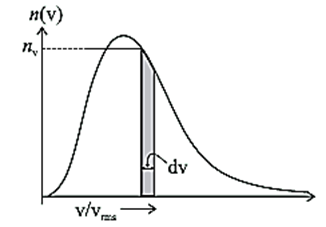
Distribution of speeds of molecules of gas : Figure shows a typical distribution of speeds for a gas at a temperature T. This is known as Maxwell's distribution of molecular speeds. Here, the shaded area nv dv is the number of molecules having speed between v and v + dv. Average values of physical quantities like \(\bar{v^2}\) can be calculated once the distribution is known.
Law of equipartition of energy
Law of equipartition of energy: For a gas in thermal equilibrium at absolute temperature T, the average energy for a molecule, associated with each quadratic term (each degree of freedom), is \(\frac12\)kBT, where kB, is the Boltzmann constant, OR
The energy of the molecules of a gas, in thermal equilibrium at a thermodynamic temperature T and containing large number of molecules, is equally divided among their available degrees of freedom, with the energy per molecule for each degree of freedom equal to \(\frac12\)kBT, where kB, is the Boltzmann constant.
The law of equipartition of energy is valid for high temperatures and not for extremely low temperatures where quantum effects become important.
Degree of freedom : Degrees of freedom of a system are defined as the total number of coordinates or independent quantities required to describe the position and configuration of the system completely.
The concept of degrees of freedom as used in the kinetic theory specifies the number of independent ways in which an atom or molecule can take up energy. It depends only on the possibilities of motion of the atom or molecule.
Gas molecules of all types have x-, y- and z-components of velocity that are entirely independent of one another. Thus, they have three ways to move in translation, i.e., three degrees of translational freedom.
Degrees of freedom for an atom : An atom (or a monatomic molecule, i.e., a molecule containing a single atom, e.g., He) treated as a point mass, has no rotational motion. Hence, it has only three degrees of translational freedom.
Degrees of freedom for a diatomic molecule : A diatomic molecule, in addition to translation, can rotate about axes perpendicular to the line connecting the atoms, as shown in Fig. but not about that line itself. Therefore, it has only two degrees of rotational freedom. Further, the two atoms may oscillate alternately toward and away from one another along the line joining them, as if connected by a spring. As a harmonic oscillator can have potential energy as well as kinetic energy, a diatomic molecule is regarded to have two degrees of vibrational freedom. Thus, at high enough temperatures, a diatomic molecule has seven degrees of freedom: three of translation, and two each of rotation and vibration.
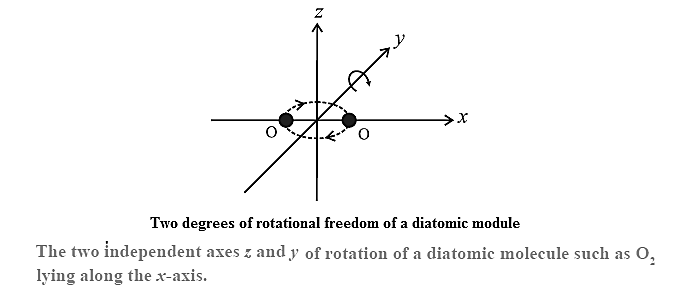
| (1) That a monatomic gas molecule does not have rotational energy, and that a diatomic molecule does not have a third rotational degree of freedom corresponding to rotation about the line joining the atoms, are explained by quantum theory.
(2) Also according to quantum theory, rotational and oscillatory motions begin at certain higher temperatures. For a molecule of a diatomic gas (like hydrogen), only translation is possible at very low temperatures (below about 100 K). As the temperature increases, rotational motion can begin; so that at room temperature a diatomic molecule has only five degrees of freedom behaving like a pair of atoms rigidly connected like a dumbbell. Oscillatory motion can begin only at quite high temperatures substantially above room temperature (usually of the order of thousands of kelvin). |
The degrees of freedom depend upon :
- the number of atoms forming a molecule
- the structure of the molecule
- the temperature of the gas
Specific Heat Capacity: When the temperature of a gas is increased, even a small rise causes considerable change in volume and pressure.
Therefore two specific heats are defined for gases, namely specific heat at constant volume CV and specific heat at constant pressure CP.
Mayer’s relation gives an expression that connects the two specific heats.
Mayer's relation between the molar specific heat of a gas at constant pressure and that at constant volume : (Q. Using the first law of thermodynamics, show that for an ideal gas, the difference between the molar specific heat capacities at constant pressure and at constant volume is equal to the molar gas constant R. ) Consider a cylinder of volume V containing H moles of an ideal gas at pressure P, fitted with a piston of area A. Suppose, the gas is heated at constant pressure which raises its temperature by dT. The gas exerts a total force F =PA on the piston which moves outward a small distance dx, see Fig. The work done by the force in moving the piston is dW = Fdx = PAdx = PdV ……….(1) where Adx = dV is the increase in volume of the gas during the expansion. dW is the work done by the gas on the surroundings as a result of the expansion. If the heat supplied to the gas is dQP and the increase in its internal energy is dE then, by the first law of thermodynamics, dQP = dE+dW = dE+PdV If CP is the molar specific heat capacity of the gas at constant pressure, dQP = nCP dT. ∴ nCPdT = dE+PdV …….(2) On the other hand, if the gas was heated at constant volume (instead of at constant pressure) from the initial state such that its temperature increases by the same amount dT, then dW = 0. Since the internal energy of an ideal gas depends only on the temperature, the increase in internal energy would again be dE. If dQV was the heat supplied to the gas in this case, by the first law of thermodynamics and the definition of molar specific heat capacity at constant volume (CV), dQV = dE = nCVdT ……. (3) From Eqs (2) and (3), ∴ nCPdT = nCVdT + PdV ∴ CP - CV = \(\frac{P}{n}\frac{dV}{dT}\) ……. (4) The equation of state of an ideal gas is PV= nRT Therefore, at a constant pressure, PdV = nRdT ∴ \(\frac{dV}{dT}\) = \(\frac{nR}{P}\) ……. (5) From Eqs. (4) and (5), CP - CV = \(\frac{P}{n}\frac{nR}{P}\) = R ……. (6) This is Mayer’ s relation between CP and CV Here, heat and work are expressed in the same units. If heat is expressed in calorie or kilocalorie and work is expressed in erg or joule, the above relation becomes CP - CV = \(\frac RJ\) where J is the mechanical equivalent of heat.
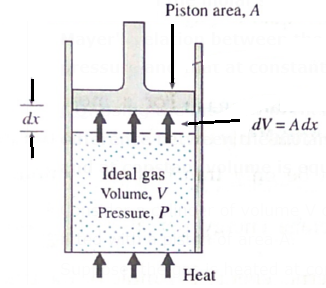
Mayer’s relation in terms of the principal specific heats, SP and SV : Mayer's relation : CP — CV = R. Let M0 = molar mass of the gas, SP=specific heat of the gas at constant pressure and SV= specific heat of the gas at constant volume. Now: CP = M0SP and CV = M0SV M0SP — M0SV = R SP —SV = \(\frac{R}{M_0}\) when heat and work are expressed in the same units. If heat is expressed in calorie or kilocalorie and work is expressed in erg or joule, we get, SP —SV = \(\frac{R}{M_0J}\) where J is the mechanical equivalent of heat. [Notes : CP= \(\frac{1}{n}\frac{dQP}{dT}\) and SP = \(\frac{1}{M}\frac{dQP}{dT}\) ∴ \(\frac{C_P}{S_P}=\frac{M}{n}=\frac{nM_0}{n}=M_0\) CP = M0SP Similarly CV = M0SV
Q. Calculate the molar specific heal of mono and diatomic gases at constant volume and constant pressure.
For a gas in thermal equilibrium at absolute temperature T, the average energy for a molecule, associated with each quadratic term (each degree of freedom), is kBT, where kB, is the Boltzmann constant. a. Monatomic gas: For a monatomic gas, each atom has only three degrees of freedom as there can be only translational motion. Hence, the average energy per atom is \(\frac 32\) kBT The total internal energy per mole of the gas is E= \(\frac 32\) NAkBT … where NA is the Avogadro number. Therefore, the molar specific heat of the gas at constant volume is CV =\(\frac{dE}{dT}\) = \(\frac 32\) NAkB = \(\frac 32\) R where R is the universal gas constant. Now, by Mayer’s relation, CP — CV = R, where CP is the specific heat of the gas at constant pressure. CP = CV +R = \(\frac 32\) R +R = \(\frac 52\) R b. Diatomic gas : Treating the molecules of a diatomic gas as rigid rotators, each molecule has three translational degrees of freedom and two rotational degrees of freedom. Hence, the average energy per molecule is 3(\(\frac 12\) kBT) + 2(\(\frac 12\) kBT)= \(\frac 52\) kBT The total internal energy of mole is \(\frac 52\) NAkBT The molar specific heat at a constant volume CV is For an ideal gas CV (monoatomic gas) = \(\frac{dE}{dT}\) = \(\frac 52\) NAkB = \(\frac 52\) R For an ideal gas CP — CV = R Where CP is the molar specific heat at constant pressure thus CP = R + \(\frac 52\) R = \(\frac 72\) R A soft or non-rigid diatomic molecule has, in addition, one frequency of vibration which contributes two quadratic terms to the energy. Hence, the energy per molecule of a soft diatomic molecule is E = 3(\(\frac 12\) kBT) + 2(\(\frac 12\) kBT) + 2(\(\frac 12\) kBT)= \(\frac 72\) kBT Therefore energy per mole of a soft diatomic module is E = \(\frac 72\) kBT × NA = \(\frac 72\) RT In this case CV = \(\frac{dE}{dT}\) = \(\frac 72\) R and CP = CV + R = \(\frac 72\) R + R = \(\frac 92\) R [Note :for monatomic gas adiabatic constant, γ = CP/CV = \(\frac 53\), for a diatomic gas γ = \(\frac 75\) or \(\frac 97\)]
Explain : Each translational and rotational degree of freedom contributes only one quadratic term to the energy but one vibrational mode contributes two quadratic terms.
With three translational degrees of freedom, the average translational energy per molecule of a gas is E (translational) = \(\frac{1}{2}m(v_x^2+v_y^2+v_z^2)\) ……. (1) where m is the mass of the molecule and vx, vy and vz are the x—, y- and z-components of the molecular velocity. A diatomic molecule has two rotational degrees of freedom. If w1 and w1 are the angular speeds about the two axes and I1 and I2 are the corresponding moments of inertia, the rotational energy of a diatomic molecule, E (rotational) = \(\frac{1}{2}(I_1ω_1^2+I_2ω_2^2)\) ……. (2) A diatomic molecule is regarded to have two degrees of vibrational freedom for the vibrational mode in which the two atoms vibrate relative to, and without affecting, the centre of mass of the molecule. Comparing this system with a vibrating body of mass m connected to a spring of force constant k, the vibrational energy has two terms corresponding to the kinetic and potential energies : E (vibrational) = \(\frac{1}{2}[m(\frac{dx}{dt})^2+kx^2]\) ……. (3) where x is the displacement from the mean position. From Eqs. (1), (2) and (3), each translational and rotational degree of freedom contributes only one quadratic term to the average energy of a gas molecule while one vibrational mode contributes two quadratic terms. For a gas at an absolute temperature T, the average kinetic energy per molecule, KE = \((\frac{1}{2}mv_x^2)+(\frac{1}{2}mv_y^2)+(\frac{1}{2}mv_z^2)\) =\(\frac{3}{2}k_bT\) As there is no preferred direction x or y or z, we have, \((\frac{1}{2}mv_x^2)=(\frac{1}{2}mv_y^2)=(\frac{1}{2}mv_z^2)\) =\(\frac{1}{2}k_bT\)
Polyatomic Gases : Gases which have molecules containing more than two atoms are termed as polyatomic gases, e.g., ammonia gas where each molecule has one N atom and three H atoms.
Each molecule of the polyatomic gas has 3 translational degrees of freedom. Only linear molecules have 2 degrees of freedom for rotation.
All other polyatomic molecules can perform rotations about three mutually perpendicular axes through their center of mass, hence they have 3 degrees of freedom for rotation also.
If the molecule is soft at high enough temperatures, it can vibrate easily with many different frequencies, say, f, because there are many interatomic bonds.
Polyatomic molecules have more than 1 degrees of freedom for different modes of vibrational motion. The number of degrees of freedom, f, for the vibrational motion of a polyatomic molecule depends on the geometric structure of the molecule i.e., the arrangement of atoms in a molecule.
According to the law of equipartition of energy, for each degree of freedom of translation and rotation, the molecule has the average energy ½kBT, but for each frequency of vibration the average energy is kBT, since each vibration involves potential energy and kinetic energy. kB is the Boltzmann constant and T is the thermodynamic temperature.
Hence expression for, (i) The energy per molecule = \(3(\frac{1}{2}k_bT)\)+\(3(\frac{1}{2}k_bT)\)+f(kBT) = (3+f)kBT (ii) The energy per mole, E = (3+f)kBTxNA = (3+f)RT (iii) CV = \(\frac{dE}{dT}\) = (3+f)R (iv) CP= CV +R = (3+f)R+R = (4+f)R (v) The adiabatic constant, λ = \(\frac{C_P}{C_V}=\frac{4+f}{3+f}\) [As f increases, λ decreases]
Useful links :
| Main Page : - Maharashtra Board Class 12-Physics - All chapters notes, solutions, videos, test, pdf.
Books : MSBSHSE -Class 12th Science Text Books – Chapter wise PDF for download Previous Chapter :Chapter-2-Mechanical properties of fluid - Online Notes Next Chapter :Chapter-4-Thermodynamics - Online Notes |
How can download this file
visit pdf store for details.
Superb page of my 12 std tnxs for this idea