Mechanical Properties of Fluid
Class-12th-Physics-Chapter-2-Maharashtra Board
Notes-Part-2
|
PART-2 1) Surface tension :
|
Surface tension : Surface tension is a unique property of liquids that arises because the net intermolecular force of attraction on the liquid molecules at or near a liquid surface differs from that on molecules deep in the interior of the liquid. This results in the tendency of the free surface of a liquid to minimize its surface area and behave somewhat like a stressed elastic membrane.
Surface tension is important in understanding the peculiar behaviour of the free surface of a liquid in many cases as illustrated below :
- Small quantities of liquids assume the form of spherical droplets, as in mist, or a mercury droplet on a flat surface. This is because the stressed surface ‘skin’ tends to contract and mould the liquid into a shape that has minimum surface area for its volume, i.e., into a sphere.
- Surface tension is responsible for the spherical shape of freely-falling raindrops and the behaviour of bubbles and soap films.
- The bristles of a paint brush cling together when it is drawn out of water or paint.
- A steel needle or a razor blade can, with care, be supported on a still surface of water which is much less dense than the metal from which these objects are made of.
- Many insects like ants, mosquitoes, water striders, etc., can walk on the surface of water.
Cohesive force : The intermolecular force of attraction between two molecules of the same material is called the cohesive force.
Example : The force of attraction between two water molecules.
Adhesive force : The intermolecular force of attraction between two molecules of different materials is called the adhesive force.
Example :The force of attraction between a water molecule and a molecule of the solid surface which is in contact with water.
Range of molecular attraction or molecular range :
Range of molecular attraction or molecular range is defined as the maximum distance between two molecules up to which the intermolecular force of attraction is appreciable.
| The intermolecular force is a short range force, i.e., it is effective over a very short range about 10-9 m. Beyond this distance, the force is negligible. The inter-molecular force does not obey inverse square law. |
Sphere of influence :The sphere of influence of a molecule is defined as an imaginary sphere with the molecule as the centre and radius equal to the range of molecular attraction.
| All molecules lying within the sphere of influence of a molecule are attracted by (as well as attract) the molecule at the centre. For molecules which lie outside this sphere, the intermolecular force due to the molecule at the centre is negligible |
Surface film : The layer of the liquid surface of thickness equal to the range of molecular attraction is called a surface film.
Free surface of a liquid : The surface of a liquid open to the atmosphere is called the free surface of the liquid.
Phenomenon of surface tension on the basis of molecular theory :
The phenomenon of surface tension arises due to the cohesive forces between the molecules of a liquid. The net cohesive force on the liquid molecules within the surface film differs from that on molecules deep in the interior of the liquid.
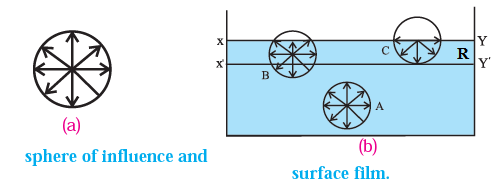
Consider three molecules of a liquid : A molecule A well inside the liquid, and molecules B and C lying within the surface film, see Fig.
The figure also shows their spheres of influence of radius R.
- The sphere of influence of molecule A is entirely inside the liquid and the molecule is surrounded by its nearest neighbours on all sides. Hence, molecule A is equally attracted from all sides, so that the resultant cohesive force acting on it is zero. Hence, it is free to move anywhere within the liquid.
- For molecule B, a part of its sphere of influence is outside the liquid surface. This part contains air molecules whose number is negligible compared to the number of molecules in an equal volume of the liquid. Therefore, molecule B experiences a net cohesive force downward.
- For molecule C, the upper half of its sphere of influence is outside the liquid surface. Therefore, the resultant cohesive force on molecule C in the downward direction is maximum.
- Thus, all molecules lying within a surface film or thickness equal to R experience a net cohesive force directed into the liquid.
- The surface area is proportional to the number of molecules on the surface. To increase the surface area, molecules must be brought to the surface from within the liquid. For this, work must be done against the cohesive forces. This work is stored in the liquid surface in the form of potential energy.
- With a tendency to have minimum potential energy, the liquid tries to reduce the number of molecules on the surface so as to have minimum surface area. This is why the surface of a liquid behaves like a stressed elastic membrane.
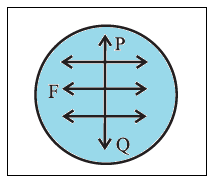
Units of surface tension : The surface tension of a liquid is defined as the tangential force per unit length, acting at right angles on either side of an imaginary line on the free surface of the liquid.
If F is the force on one side of a line of length l, drawn on the free surface of a liquid, the surface tension (T) of the liquid is T=F/l
The CGS unit of surface tension : The dyne per centimetre (dyn/ cm) or, equivalently, the erg per square centimetre (erg/cm2).
The Sl unit of surface tension : The newton per metre (N/ m) or, equivalently, the joule per square metre (J/m2).
Q. Obtain the dimensions of surface tension.
Surface tension is force per unit length.
∴ [Surface tension] = [force] / [length] = [ML1T−2] / [M°L1T°] = [ML° T−2]
Surface tension is also equal to the surface energy per unit surface area of a liquid.
[Surface tension] = [energy] / [area] = [work] / [area] = ([force] [displacement])/[area]
= ([ML1T−2] [M°L1T°]) / [M°L2T°] = [ML° T−2]
Surface energy : The surface energy is defined as the extra (or increased) potential energy possessed by the molecules in a liquid surface with an isothermal increase in the surface area of the liquid.
- A liquid exerts a resultant cohesive force on every molecule of its surface, trying to pull it into the liquid. To increase the surface area, it is necessary to bring more molecules from inside the liquid to the liquid surface. For this, external work must be done against the net cohesive forces on the molecules.
- This work is stored in the liquid surface in the form of potential energy.
- This extra potential energy that the molecules in the liquid surface have is called the surface energy.
- Thus, the molecules of a liquid in the surface film possess extra energy.
Dimensions : [surface energy] =[ML2T−2]
SI unit : the joule (J).
Q. Why is the surface tension of paints and lubricating oils kept low?
For better wettability (surface coverage), the surface tension and angle of contact of paints and lubricating oils must be low.
Relation between the surface tension and surface energy of a liquid:
Suppose a soap film is isothermally stretched over the area enclosed by a U-shaped frame ABCD and a cross-piece RQ that can slide smoothly along the frame, as shown in the figure. Let T be the surface tension of the soap solution and l, the length of wire RQ in contact with the soap film.
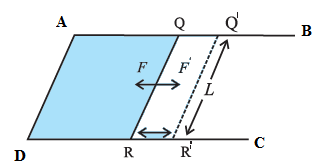
The film has two surfaces, both of which are in contact with the wire. The film tends to contract by exerting a force on wire RQ. As each surface exerts a force Tl, the net force on the wire is 2Tl.
Suppose that wire RQ is pulled outward very slowly through a distance dx to the position R’Q' by an external force of magnitude 2Tl. The work done by the external force against the force due to the film is
W = applied force x displacement
∴ W=Fdx = 2Tldx (… F=2Tl)
This work is stored in the unit surface area in the form of potential energy. This potential energy is called the surface energy.
Due to the displacement dx, the surface area of the film increases. As the film has two surfaces, the increase in its surface area is
A = 2ldx
Thus, the work done per unit surface area is
\frac{W}{A} =\frac{2Tldx}{2ldx} = T
Thus, the surface energy per unit area of a Liquid is equal to its surface tension.
Angle of contact : The angle of contact for a liquid-solid pair (a liquid in contact with a solid) is defined as the angle between the surface of the solid and the tangent drawn to the free surface of the liquid at the extreme edge of the liquid, as measured through the liquid.
Characteristics of angle of contact :
- It depends upon the nature of the liquid and solid in contact, and is constant for a given liquid—solid pair, other factors remaining unchanged.
- It depends upon the medium (gas) above the free surface of the liquid.
- It is independent of the inclination of the solid to the liquid surface.
- It changes with surface tension and, hence, with the temperature and purity of the liquid.
Characteristics of the angle of contact in :
(i) The angle of contact in the case of a liquid which completely wets.
For a liquid, which completely wets the solid, the angle of contact is zero.
For example, pure water completely wets clean glass. Therefore, the angle of contact at the water glass interface is zero

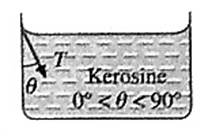
(ii) The angle of contact in the case of a liquid which partially wets
For a liquid which partially wets the solid, the angle of contact is an acute angle.
For example, kerosine partially wets glass, so that the angle of contact is an acute angle at the kerosine-glass interface
(iii) The angle of contact in the case of a liquid which does not wet the solid.
For a liquid which does not wet the solid, the angle of contact is an obtuse angle.
For example, mercury does not wet glass at all, so that the angle of contact is an obtuse angle at the mercury-glass interface.
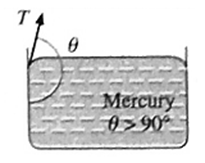
(iv) The angle of contact for a given liquid solid pair is constant at a given temperature, provided the liquid is pure and the surface of the solid is clean.
Formation of concave and convex surface of a liquid on the basis of molecular theory.
OR
(Q. why the free surface of some liquids in contact with a solid is not horizontal.?)
For a molecule in the liquid surface which is in contact with a solid, the forces on it are largely the solid-liquid adhesive force FA = PA and the liquid- liquid cohesive force FC = PC, FA is normal to the solid surface and FC is at 45° with the horizontal See Fig. The free surface of a liquid at rest is always perpendicular to the resultant FR = PR of these forces
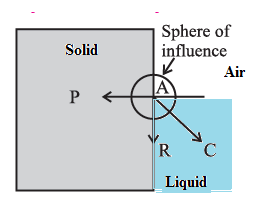
If FC = \sqrt{2} FA, FR is along the solid surface, the contact angle is 90° and the liquid surface is horizontal at the edge where it meets the solid, as in above Fig. In general this is not so, and the liquid surface is not horizontal at the edge.
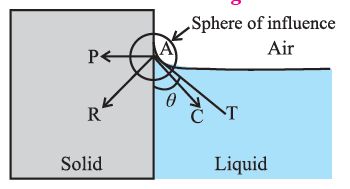
For a liquid which completely wets the solid (e.g. pure water in contact with clean glass), FC << FA. For a liquid which partially wets the solid (e.g., kerosene or impure water in contact with glass), FC < \sqrt{2}FA
If FC << FA or if FC < \sqrt{2}FA, the contact angle is correspondingly zero or acute and the liquid surface curves up and acquires a concave shape until the tangent PT is tangent to FR ref. below Fig.
If FC > \sqrt{2}FA, the contact angle is obtuse and the liquid surface curves down and acquires a convex shape until the tangent PT is tangent to FR, see below Fig.
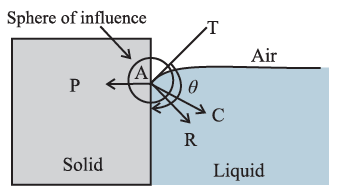
Q. State the conditions for concavity and convexity of a liquid surface where it is in contact with a solid. (1 mark)
For a molecule in the liquid surface which is in contact with a solid, the forces on it are largely
(i) the solid-liquid adhesive force FA, normal and into the solid surface and (ii) the liquid-liquid cohesive force E at nearly 45° with the horizontal.
if FC << FA or if FC < \sqrt{2}FA, the contact angle is correspondingly zero or acute and the liquid surface is concave with the solid.
If FC > \sqrt{2}FA, the contact angle is obtuse and the liquid surface curves down, i.e., convex, with the solid.
Shape of a liquid drop on solid surface in terms of interfacial tensions.
A liquid surface, in general, is curved where it meets a solid. The angle between the solid surface and the tangent to the liquid surface at the extreme edge of the liquid, as measured through the liquid, is called the angle of contact.
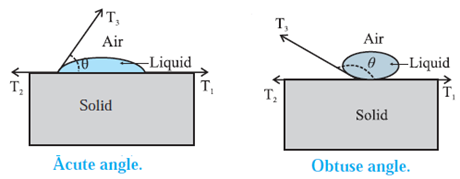
Figure shows the interfacial tensions that act in equilibrium at the common point of the liquid, solid and gas (air + vapour).
T1 = the liquid-solid interfacial tension
T2 = the solid-gas interfacial tension
T3 = the liquid-gas interfacial tension
θ = the angle of contact for the liquid-solid pair is the angle between T1 and T3,
The equilibrium force equation (along the solid surface) is
T3 cos θ + T1 – T2 = 0
∴ cos θ =\frac{T_2-T_1}{T_3} ......... (1)
Case (1) : If T2 > T1 , cos θ is positive and contact angle 0 < 90°, so that the liquid wets the surface.
Case (2) : If T2 < T1, cos θ is negative and q is obtuse, so that the liquid is non-wetting.
Case (3) : If T2 — T1, ≅ T3, cos θ = 1 and θ ≅ 0°.
Case (4) : If T2 — T1, > T3, cos θ will be greater than 1 which is impossible, so that there will be no equilibrium and the liquid will spread over the solid surface.
Q State the expression for the angle of contact in terms of interfacial tensions? (1 mark)
cos θ = \frac{T_2-T_1}{T_3}, where θ is the angle of contact for a liquid-solid pair,
T1 = the liquid-solid interfacial tension
T2 = the solid-gas interfacial tension
T3 = the liquid-gas interfacial tension
Q. ln terms of interfacial tension, when is the angle of contact acute ? (1 mark)
The angle of contact is acute when the solid-gas (air + vapour) interfacial tension is greater than the liquid-solid interfacial tension.
Q. In terms of interfacial tensions, when is the angle of contact obtuse ? (1 mark)
The angle of contact is obtuse when the solid-gas (air+vapour) interfacial tension is less than the liquid-solid interfacial tension.
Q. Explain : Pure water on a clean glass surface tends to spread out, while mercury on the same surface tends to form a drop. (3 marks)

For pure water on a clean glass surface, T2 — T1 ≅ T3, so that cosθ=1 and θ ≅ 0° i.e., pure water completely wets the surface. Thus, when a drop of pure water is put on a clean glass surface, it flattens out.
For mercury on the same surface, T2 < T1, so that cosθ is negative and θ is obtuse, i.e., mercury is non-wetting. Thus, a small drop of mercury on a clean glass surface is almost spherical.
Factors affecting a liquid-solid angle of contact :
(1) The nature of the liquid and the solid in contact,
(2) Impurities in the liquid,
(3) Temperature of the liquid.
Effect of impurity :
(i) The angle of contact or the surface tension of liquid increases with dissolved impurities like common salt. For dissolved impurities, the angle of contact (or surface tension) increases linearly with the concentration of the dissolved materials.
(ii) It decreases with sparingly soluble substances like phenol or alcohol. A detergent is a surfactant whose molecules have hydrophobic and hydrophilic ends, the hydrophobic ends decrease the surface tension of water. With reduced surface tension, the water can penetrate deep into the fibres of a cloth and remove stubborn stains.
(ii) It decreases with insoluble surface impurities like oil, grease or dust. For example, mercury surface contaminated with dust does not form perfect spherical droplets till the dust is removed.
Effect of Temperature :
The surface tension of a liquid decreases with increasing temperature of the liquid. For small temperature differences, the decrease in surface tension is nearly directly proportional to the temperature rise.
If T and T0 are the surface tensions of a liquid at temperatures q and 0°C, respectively, then
T=T0(1 − αθ) where α is a constant for a given liquid.
The surface tension of a liquid becomes zero at its critical temperature. The surface tension increases with increasing temperature only in case of molten copper and molten cadmium.
Q. Why cold wash is recommended for new cotton fabrics while hot wash for removing stains ? (1 mark)
- Cold wash is recommended for new/ coloured cotton fabrics. Cold water, due to its higher surface tension, does not penetrate deep into the fibres and thus does not fade the colours.
- Hot water, because of its lower surface tension, can penetrate deep into fabric fibres and remove tough stains.
Pressure difference across a curved liquid surface.:
Every molecule lying within the surface film of a static liquid is pulled tangentially by forces due to surface tension. The direction of their resultant,\vec f_r on a molecule depends upon the shape of that liquid surface and decides the cohesion pressure at a point just below the liquid surface.
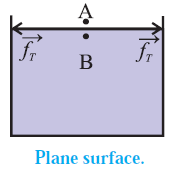
Consider two molecules, A and B, respectively just above and below the free surface of a liquid. So the level difference between them is negligibly small and the atmospheric pressure on both is the same, po, Let \vec f_A be the downward force on A and B due to the atmospheric pressure.
(i) If the free surface of a liquid is horizontal, the resultant force \vec f_r on molecule B is zero, see Fig. Then, the cohesion pressure is negligible and the net force on A and B is \vec f_A . The pressure difference on the two sides of the liquid surface is zero.
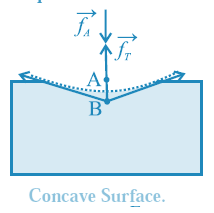
(ii) If the free surface of a liquid is concave, the resultant force \vec f_r on molecule B is outwards (away from the liquid), see below Fig. opposite to \vec f_A
Then, the net force on B is less than \vec f_A, and the cohesion pressure is decreased. The pressure above the concave liquid surface is greater than that just below the liquid surface.
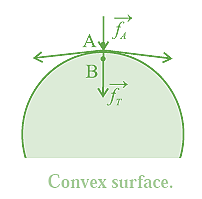
(iii) If the free surface of a liquid is convex, the resultant force \vec f_r on molecule B acts inwards (into the liquid), see below Fig. in the direction of .\vec f_A
Then, the net force on B is greater than \vec f_A and the cohesion pressure is increased. The pressure below the convex liquid surface is greater than that just above the liquid surface.
Laplace's law for a spherical membrane. :
(Q. Derive an expression for the excess pressure inside a liquid drop.)
Consider a spherical drop as shown in Fig.
Let pi be the pressure inside the drop and p0 be the pressure outside it. As the drop is spherical in shape, the pressure, pi, inside the drop is greater than p0, the pressure outside.
Therefore, the excess pressure inside the drop is pi - p0.
Let the radius of the drop increase from r to r + Δr, where Δr is very small,
so that the pressure inside the drop remains almost constant.
Let the initial surface area of the drop be
A1 = 4πr2,
and the final surface area of the drop be
A2 = 4π (r+Δr)2
∴ A2 = 4π (r2 + 2rΔr + Δr2)
∴ A2 = 4π r2 + 8πrΔr + 4πΔr2
As Δr is very small, Δr2 can be neglected,
∴ A2 = 4πr2 + 8πrΔr
Thus, increase in the surface area of the drop is
dA = A2 – A1 = 4πr2 + 8πrΔr - 4πr2 = 8πrΔr --- (1)
Work done in increasing the surface area by dA is stored as excess surface energy.
∴ dW = TdA= T (8πrΔr) --- (2)
This work done is also equal to the product of the force F which causes increase in the area of the bubble and the displacement Δr which is the increase in the radius of the bubble.
∴ dW = FΔr --- (3)
The excess force is given by,
(Excess pressure) × (Surface area)
∴ F = (pi – p0) 4πr2 --- (4)
Equating Eq. (2) and Eq. (3), we get,
T(8prΔr) = (pi – p0) 4πr2 Δr
∴ (pi – p0) = \frac{2T}{r} --- (5)
This equation gives the excess pressure inside a drop. This is called Laplace’s law of a spherical membrane or Young Laplace Equation in spherical form
Q. Derive an expression for the excess pressure inside a soap bubble. OR
Derive Laplace’s law for spherical membrane of a bubble due to surface tension. (3 marks)
Consider a small, spherical, thin-filmed soap bubble with a radius r. Let the pressure outside the drop be po and that inside be pi. A soap bubble in air is like a spherical shell and has two gas-liquid interfaces. Hence, the surface area of the bubble is
A = 4πr2 …..(1)
Hence, with a hypothetical increase in radius by an infinitesimal amount Δr, the differential increase in surface area and surface energy would be
dA = 16πrΔr and
dW = T.dA = T(16πrΔr) …….(2)
We assume that Δr is so small that the pressure inside remains the same, equal to pi. All parts of the surface of the bubble experiences an outward force per unit area equal to pi – p0.
Therefore, the work done by this outward pressure-developed force against the surface tension force during the increase in radius Δr is
dW= (Excess pressure) × (Surface area).Δr
= (pi – p0) 4πr2 Δr …….(3)
From Eqs. (2) and (3),
(pi – p0) 4πr2 Δr = T(16πrΔr)
∴ pi – p0 = \frac{4T}{r} --- (4) which is the required expression.
[Note ; The excess pressure inside a drop or bubble is inversely proportional to its radius : the smaller the bubble radius, the greater the pressure difference across its wall.]
Capillary Action :
A tube of narrow bore (i.e. very small diameter) is called a capillary tube. The word capillary is derived from the Latin capillus meaning hair, capillaris in Latin means ‘like a hair’.
If a capillary tube is just partially immersed in a wetting liquid the liquid rises in the capillary tube. This is railed capillary rise.
If a capillary tube is just partially immersed in a non-wetting liquid, the liquid falls in the capillary tube. This is called capillary depression.
The rise of a wetting liquid and fall of non-wetting liquid in a capillary tube is called capillarity.
Applications of capillarity :
- A blotting paper or a cotton cloth absorbs water, ink by capillary action.
- Oil rises up the wick of an oil lamp and sap rises up xylem tissues of a tree by capillarity.
- Ground water rises to the open surface through the capillaries formed in the soil. In summer, the farmers plough their fields to break these capillaries and prevent excessive evaporation.
- Water rises up the crevices in rocks by capillary action. Expansion and contraction of this water due to daily and seasonal temperature variations cause the rocks to crumble.
[Note : The rise of sap is due to the combined action of capillarity and transpiration. The transpiration pull considered to be the major driving force for water transport throughout a plant.]
Phenomenon of capillarity (Capillary action ):
(1) When a capillary tube is partially immersed a wetting liquid, there is capillary rise and liquid meniscus inside the tube is concave, as shown in Fig. (A).
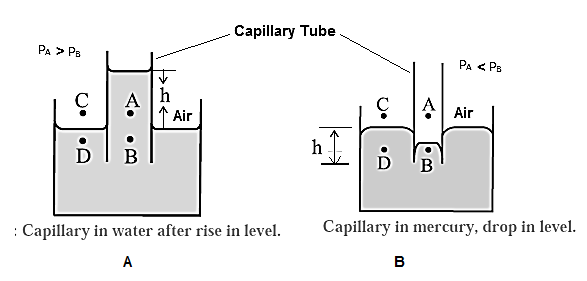
Consider four points A, B, C, D, of which point is just above the concave meniscus inside the capillary and point B is just below it. Points C and D are just above and below the free liquid surface outside.
Let PA, PB, PC and PD be the pressures at point A, B, C and D, respectively.
Now, PA = PC = atmospheric pressure
The pressure is the same on both sides of the free surface of a liquid, so that
PC = PD
∴ PA = PD
The pressure on the concave side of a meniscus is always greater than that on the convex side, so that
PA > PB
∴ PD > PB (….PA = PD)
The excess pressure outside presses the liquid up the capillary until the pressures at B and D (at the same horizontal level) equalize, i.e., PB becomes equal to PD. Thus, there is a capillary rise.
(2) For a non-wetting liquid, there is capillary depression and the liquid meniscus in the capillary tube is convex, as shown in Fig. (B).
Consider again four points A, B, C and D when the meniscus in the capillary tube is at the same level as the free surface of the liquid. Points A and B are just above and below the convex meniscus.
Points C and D are just above and below the free liquid surface outside.
The pressure at B (PB) is greater than that at A(PA). The pressure at A is the atmospheric pressure H and at D, PD @ H = PA. Hence, the hydrostatic pressure at the same levels at B and D are not equal,
PB > PD.
Hence, the liquid flows from B to D and the level of the liquid in the capillary falls. This continues till the pressure at B’ is the same as that D’, that is till the pressures at the same level are equal.
An expression for capillary rise for a liquid having a concave meniscus.
Consider a capillary tube of radius r partially immersed into a wetting liquid of density p. Let the capillary rise be h and q be the angle of contact at the edge of contact of the concave meniscus and glass (Fig)..
If R is the radius of curvature of the meniscus then from the figure, r=R cosθ.
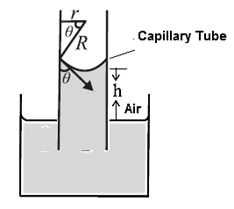
Surface tension T is the tangential force per unit length acting along the contact line. It is directed into the liquid making an angle θ with the capillary wall. We ignore the small volume of the liquid in the meniscus. The gauge pressure within the liquid at a depth h, i.e. at the level of the free liquid surface open to the atmosphere, is
P— Po = ρgh ………. (1)
By Laplace’s law for a spherical membrane, this gauge pressure is
P— Po = 2T/R …….(2)
hρg = 2T/R = \frac{2Tcosθ}{r}
∴ h = \frac{2Tcosθ}{rρg}…….(3)
Thus, narrower the capillary tube, the greater is the capillary rise.
From Eq. (3),
T= \frac{hrρg}{2Tcosθ}………(4)
Equations (3) and (4) are also valid for capillary depression h of a non-wetting liquid. In this case, the meniscus is convex and θ is obtuse. Then, cosθ is negative but so is h, indicating a fall or depression of the liquid in the capillary. T is positive in both cases.
[For capillary rise, Eq. (3) is also called the ascent formula. ]
| << Previous Part | Next Part >> |
Click on below link to get PDF from store:
MSBSHSE-Class-12-Physics-Chapter-2-Mechanical Properties of Fluid-Book
MSBSHSE-Class-12-Physics-Chapter-2-Mechanical Properties of Fluid-Notes
MSBSHSE-Class-12-Physics-Chapter-2-Mechanical Properties of Fluid-Solution
Useful links :
| Main Page : - Maharashtra Board Class 12-Physics - All chapters notes, solutions, videos, test, pdf.
Books : MSBSHSE -Class 12th Science Text Books – Chapter wise PDF for download Previous Chapter :Chapter-1-Rotational Dynamics - Online Notes Next Chapter :Chapter-3-Kinetic Theory of Gases and radiation -Online Notes |