Mechanical Properties of Fluid
Class-12th-Physics-Chapter-2-Maharashtra Board
Notes-Part-3
|
PART-3 Fluids in motion Critical velocity and Reynolds number
Stokes’ Law
Equation of continuity Bernoulli equation, Applications |
Fluids in motion
Hydrodynamics : Hydrodynamics is the branch of physics that deals with fluid dynamics, i.e., the study of fluids in motion. Since the most basic fluid motion is highly complex, we consider only ideal fluids-non-viscous and incompressible, i.e., fluids whose internal friction is negligible and density is constant throughout.
Steady flow : When a liquid flows slowly over a surface or through a pipe such that its velocity or pressure at any point within the fluid is constant, it is said to be in steady flow.
Streamline : Consider point A, as shown in Fig., within a fluid. The velocity v at A does not change with time.
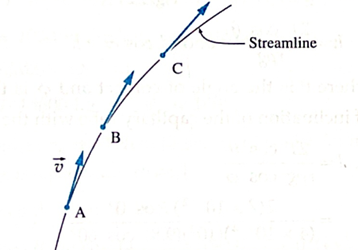
Hence, every particle passes point A with the same speed and in the same direction. The same is true about the other points such as B and C. A curve which is tangent or parallel to the velocity of the fluid particles at every point will be the path of every particle arriving at A. It is called a streamline. A fluid particle cannot cross a streamline but only flow along it.
Streamline flow : When a liquid flows slowly over a surface or through a pipe with a velocity less than a certain critical velocity, the motion of its molecules is orderly. All molecules passing a given point proceed with the same velocity. This kind of fluid motion is called streamline or steady flow.
Examples : Smoke rising from an incense stick inside a wind-less room, air flow around a car or aeroplane in motion are some examples of streamline flow, Fish, dolphins, and even massive whales are streamlined in shape to reduce drag. Migratory birds species that fly long distances often have particular features such as long necks, and flocks of birds fly in the shape of a spearhead as that forms a streamlined pattern.
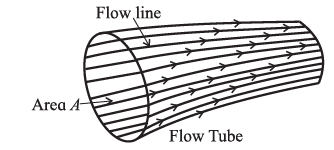
Flow tube: A bundle of adjacent streamlines form a tube of flow or flow tube through which the fluid is flowing. In a flow tube, where the streamlines are close together the velocity is high, and where they are widely separated, the fluid is moving slowly.
No fluid can cross the boundary of a tube of flow.
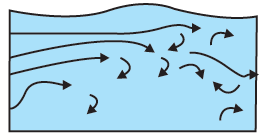
Turbulent flow : Turbulent flow or turbulence is a non-steady fluid flow in which streamlines and flow tubes change continuously. It has two main causes.
- First, any obstruction or sharp edge, such as in a tap, creates turbulence by imparting velocities perpendicular to the flow.
- Second, if the speed with which a fluid moves relative to a solid body is increased beyond at certain critical velocity the flow becomes unstable or one of extreme disorder.
In both cases, the fluid particles still move in general towards the main direction as before. But now all sorts of secondary motions cause them to cross and recross the main direction continuously. The orderly streamlines break up into eddies or vortices and the result is turbulence. In a turbulent flow regions of fluid moves in irregular, colliding paths, resulting in mixing and swirling (Fig.)
Example : Turbulence is commonly seen in washing machines and kitchen mixers. Turbulence in these devices is desirable because it causes mixing.
Advantages of turbulence :
- The turbulent agitation in the layers of air near the ground and in the waters of the oceans cause the diffusion of heat and matter, and provide a mechanism for very efficient mixing. Without turbulence, the air at the ground level would either be intolerably hot or very cold and either extremely humid or very dry or smoke would cling to the ground for days.
- Turbulence is also extremely important for bird and insect flights, and for air pollination.
Disadvantages of turbulence :
- Turbulence is undesirable in mechanical flights (aircraft), water navigation, ballistics, high-speed cars, etc., because of increased resistance.
- To reduce turbulence, and hence fluid resistance, these bodies are given a streamlined or aerodynamic shape.
| Streamline flow | Turbulent flow |
| 1-The steady flow of a fluid, with velocity less than certain critical velocity is called streamline or laminar flow.
2-In a streamline flow, the velocity of a fluid at a given point is always constant. 3-Streamlines do not change and never intersect. 4-The fluid flow is laminar over a surface, and is in the form of coaxial cylinders through a pipe. |
1- A non-steady irregular fluid flow in which streamlines and flow tubes change continuously with a velocity greater than certain critical velocity.
2-In a turbulent flow, the velocity of a fluid at any point does not remain constant. 3-Streamlines and flow tubes change continuously. 4-Fluid particles still move in general towards the main direction as before. But now all sorts of secondary motions cause eddies or vortices. |
Reynolds number: Osborne Reynolds found that if the free-stream velocity of a fluid increases when it moves relative to a solid body, a point is reached where the steady flow becomes turbulent. From experiments, he found that the transition from steady to turbulent flow depends on the value of the quantity \frac{v_0ρd}{η}
where vo is the free-stream velocity, d is some characteristic dimension of the system, ρ the density of the fluid and η its coefficient of viscosity.
For a sphere in a fluid stream, d is its diameter; for water in a pipe, d is the pipe diameter.
This dimensionless number, defined as
Re = \frac{v_0ρd}{η} is called the Reynolds number.
The flow of a fluid, whether streamline or turbulent, is differentiated on the basis of velocity of the flow. The velocity beyond which a streamline flow becomes turbulent is called critical velocity.
According to Osborne Reynolds critical velocity is given by
v_c = \frac{ηR_e}{ρd}
In a system of particular geometry, transition from steady to turbulent flow is given by a certain value of the Reynolds number called the critical Reynolds number.
Steady flow takes place for Re up to about 1000.
For 1000 < Re < 2000, there is a transition region in which the flow is extremely sensitive to all sorts of small disturbances. For Re > 2000, the flow is completely turbulent.
Viscosity: Suppose a constant tangential force is applied to the surface of a liquid. Under this shearing force, the liquid begins to flow. The motion of a thin layer of the liquid at the surface, relative to a layer below, is opposed by fluid friction. Because of this internal, fluid friction, horizontal layers of the liquid flow with varying velocities.
This also happens in a gas. When a solid surface is moved through a gas, a thin layer of the gas moves with the surface. But its motion relative to a layer away is opposed by fluid friction.
The resistance to relative motion between the adjacent layers of a fluid is known as viscosity.
Viscous drag : When a fluid flows past a solid surface, or when a solid body moves through a fluid, there is always a force of fluid friction opposing the motion. force of fluid friction is called the drag force or viscous drag.
It is a property of the fluid. The resistive force in fluid motion is called the viscous drag.
Reason of viscous drag : In liquids, the viscous drag is due to short range molecular cohesive forces while in gases it is due to collisions between fast moving molecules.
- For laminar flow in both liquids and gases, the viscous drag is proportional to the relative velocity between the layers, provided the relative velocity is small.
- For turbulent flow, the viscous drag increases rapidly and is proportional to some higher power of the relative velocity.
Velocity gradient: The rate of change of velocity (dv) with distance (dx) measured from a stationary layer is called velocity gradient (dv/dx).
When a fluid flows past a surface with a low velocity, within a limiting distance from the surface, its velocity varies with the distance from the surface, see Fig. The layer in contact with the surface is at rest relative to the surface. Starting outwards from the surface, the next layer has an extremely small velocity; each successive layer has a slightly higher velocity than its inner neighbour, as shown.
Finally, a layer is reached which has approximately the full, or free-stream, velocity v0 of the fluid.
The situation is reversed if a body is moving in a stationary fluid : the fluid velocity reduces as the distance of a layer from the body increases. Thus, the velocity in each layer increases with its distance from the surface.
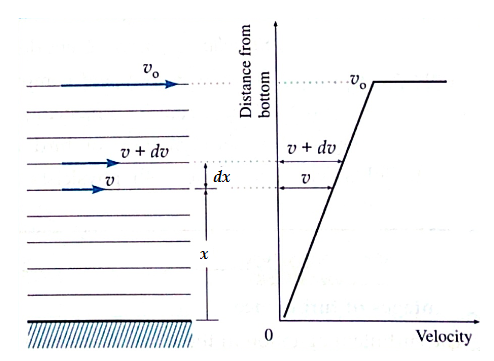
Consider the layer of thickness dx at x from the solid surface. Let v and v + dv be the velocities of the fluid at the base and upper edge of this layer.
The change in velocity across the layer is dv.
Therefore, the rate at which the velocity changes between the layers is dv/dx. This is called the velocity gradient.
Newton's law of viscosity : ln a steady flow of a fluid past a solid surface, a velocity profile is set up such that the viscous drag per unit area on a layer is directly proportional to the velocity gradient.
When a fluid flows past a solid surface in a streamline flow or when a solid body moves through a fluid, the force of fluid friction opposing the motion is called the viscous drag. The magnitude of the viscous drag of a fluid is given by Newton's law of viscosity.
If dv/dx is the velocity gradient, the viscous drag per unit area on a layer,
\frac{F}{A}∝\frac{dv}{dx}
∴\frac{F}{A} = η\frac{dv}{dx}
where the constant of proportionality, η is called the coefficient of viscosity of the fluid.
The coefficient of viscosity of a fluid is defined as the viscous drag per unit area acting on a fluid layer per unit velocity gradient established in a steady flow.
SI unit : one pascal-second (abbreviated Pa-s),
1Pa.s =1 N-m-2s
CGS unit : dyne.cm-2s, called the poise [symbol P, named after Jean Louis Marie Poiseuille (1799-1869), French physician].
η = [ML-1T-1]
Stokes’ Law: “The viscous force (Fv) acting on a small sphere falling through a viscous medium is directly proportional to the radius of the sphere (r), its velocity (v) through the fluid, and the coefficient of viscosity (η) of the fluid”.
Fv ∝ η r v
The empirically obtained constant of proportionality is 6p .
Fv = 6π η r v
This is the expression for viscous force acting on a spherical object moving through a viscous medium. The above formula can be derived using dimensional analysis.
Derivation : Since the viscous force Fv depends on η, v and v0
we can write
Fv = —bηα rβ v0γ
where b is a dimensionless proportionality constant.
Therefore,
[ Fv] = [η ] α [r ] β [v0 ] γ
With [η ] = ML—1T—1, [r ] = L, [Fv ] = ML1T—2 and [v0 ] = LT—1, we get,
ML1 T—2 = (ML—1T—1)α (L) β (LT—1) γ
∴ ML1 T—2 = Mα-L-α+β +γ T-α-γ
Homogeneity of the above dimensional equation requires that
α =1, -α+β +γ =1, -α-γ=-2
On solving, we get,
γ= -α + 2 =-1+2=1
β =1+α-γ = 1+1-1=1
Thus
α=β=γ=1
Fv = -bη r v
inserting the value of b from theory and experiments,
Fv = -6π η r v
This is called Stokes’ law, after Sir George Gabriel Stokes (1819-1903), British physicist and mathematician.
Terminal speed of a body falling through a viscous fluid and expression for the terminal speed :
Consider a small sphere of radius r, falling through a fluid with coefficient of viscosity η. Initially, as the sphere falls through the fluid under gravity, its speed increases. According to Stokes’ law, the magnitude f of the viscous force on the falling sphere is proportional to its speed v. The direction of this force is upward since the velocity of the sphere is downward. Also, the fluid exerts an upthrust or buoyant force on the sphere. As soon as the speed reaches a value, v1, the magnitude of f becomes equal to that of the gravitational force on the sphere minus the upthrust. Then, the net force acting on the sphere becomes zero. It’s subsequent downward motion is at this constant speed. This is called its terminal speed : v1 represents the highest speed which a body can attain when freely falling through a fluid with coefficient of viscosity η.

If the sphere and the fluid have densities r and rL, respectively, the total downward force on the sphere is the sum of the downward gravitational force and the upward buoyant force.
Viscous force = gravitational force—buoyant force
= mg - mLg
where m = mass of the sphere =\frac{4}{3}πr^3ρ and
mL = mass of the liquid displaced = .\frac{4}{3}πr^3ρ_L
At its terminal speed v1, the magnitude of the viscous force by Stokes’ law is
Fv = 6π η r v1
∴ 6π η r v1 = \frac{4}{3}πr^3(ρ-ρ_L)
∴ v_1=\frac{2}{9}\frac{r^2(ρ-ρ_L)}{η}g
[Note : Theoretically, v —> v1 as time t —> ∞ In practice, if η is appreciable, then v tends to v1 in a very small time interval.]
Equation of continuity
Volume flow rate : The volume of fluid passing by a given location per unit time through an area is called the volume flow rate. or simply flow rate Q.
Q = dV/dt
Consider an ideal fluid flowing with velocity v through a uniform flow tube of cross section A. lf, as shown in Fig. the shaded cylinder of fluid of length x and volume V flows past point P in time t,

v=\frac{dx}{dt} and V = Ax
Then the volume flow rate is
Q=\frac{dV}{dt}=\frac{d}{dt}Ax=A\frac{dx}{dt}=Av
which is the required relation.
The SI unit for volume flow rate is the cubic metre per second (m3/s).
Another common unit in SI is liter/minute (L/min)
Mass flow rate or mass flux : The mass of fluid passing by a given point per unit time through an area is called the mass flow rate dm/dt
See above fig.
Consider an ideal fluid of density ρ flowing with velocity v through a uniform flow lube of cross section A. If as shown an Fig the shaded cylinder of fluid of length x and volume V flows past point P in time t,
v=\frac{dx}{dt} and V = Ax
Then the mass flow rate is
Q=\frac{d(ρV)}{dt}=ρ\frac{d}{dt}Ax=ρA\frac{dx}{dt}=ρAv
which is the required relation.
Flow speed is inversely proportional to the cross-sectional area of a flow tube :
Consider a fluid in steady or streamline flow. The velocity of the fluid within a flow tube, while everywhere parallel to the tube, may change its magnitude.
- Suppose the velocity is v1 at point P and v2 at point Q.
- If A1 and A2 are the cross-sectional areas of the tube and ρ1, and ρ2 are the densities of the fluid at these two points, the mass of the fluid passing per unit time across A1 is A1ρ1 v1 and that passing across A2 is A2ρ2v2
- Since no fluid can enter or leave through the boundary of the tube, the conservation of mass requires
A1ρ1 v1 = A2ρ2v2 …..(1)
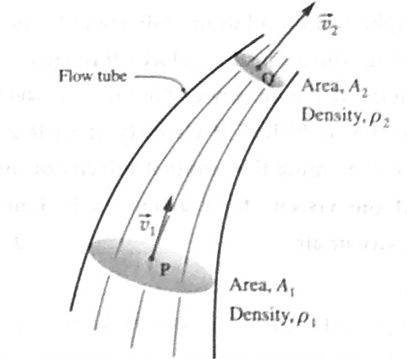
Equation (1) is called the equation of continuity of flow. It holds true for a compressible fluid, (like all gases) tor which the density of the fluid may differ from point to point in a tube of flow. For an incompressible fluid (like all liquids), ρ1 = ρ2 and eq. (1) takes the simpler form
A1 v1 = A2v2 ……. (2)
∴ v1/ v2 = A2/A1
that is the flow speed is inversely proportional to the cross-sectional area of a flow tube. Where the area is large the speed of flow is small, and vice versa.
Equations (2) is the equation of Continuity for an incompressible fluid for which density is constant throughout.
Q. Explain why flow speed is greatest where streamlines are closest together.
By the equation of continuity, the flow speed is inversely proportional to the area of cross section of a flow tube. Where the area of cross section is small, i.e., streamlines are close, the flow speed is large and vice versa.
Expression for conservation of mass starting from the equation of continuity :
Consider a fluid in steady or streamline flow, that is its density is constant. The velocity of the fluid within a flow tube, while everywhere parallel to the tube, may change its magnitude.
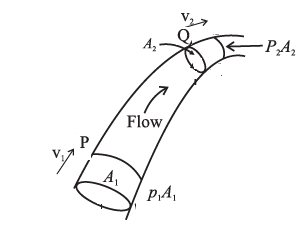
Suppose the velocity is v1 at point P and v2 at point. Q. If A1, and A2, are the cross-sectional areas of the tube at these two points,
the volume flux across A1\frac{d}{dt}(V1) = A1v1
and that across A2\frac{d}{dt}(V2) =A2v2
By the equation of continuity of flow for a fluid,
A1v1 = A2v2
i.e. \frac{d}{dt}(V1) = \frac{d}{dt}(V2)
If ρ1 and ρ2, are the densities of the fluid at P and Q, respectively, the mass flux across A1,
\frac{d}{dt}(m1) = \frac{d}{dt}(ρ1v1) = A1ρ1v1
and that across A2, \frac{d}{dt}(m2) = \frac{d}{dt}(ρ2v2) = A2ρ2v2
Since no fluid can enter or leave through the boundary of the tube, the conservation of mass requires the mass fluxes to be equal, i.e.
\frac{d}{dt}(m1) = \frac{d}{dt}(m2)
A1ρ1v1= A2ρ2v2
i.e. Aρv = constant
is the required expression.
Bernoulli equation, Applications
Bernoulli's principle: Where the velocity of an ideal fluid in streamline flow is high, the pressure is low, and where the velocity of a fluid is low, the pressure is high. OR
At every point in the streamline flow of an ideal (i.e., non-viscous and incompressible) fluid, the sum of the pressure energy, kinetic energy and potential energy of a given mass of the fluid is constant at every point.
Note: The above principle is equivalent to a statement of the law of conservation of mechanical energy as applied to fluid mechanics. It was published in 1738 by Daniel Bernoulli (1700-82), Swiss mathematician.
Bernoulli's equation of fluid flow : Consider an ideal fluid incompressible and non-viscous of density r flowing along a flow tube of varying cross section. The system under consideration is the flow tube between points 1 and 2, and the Earth (Fig.). From the continuity equation it follows that pressure and speed must be different in regions of different cross section. If the height also changes, there is an additional pressure difference.
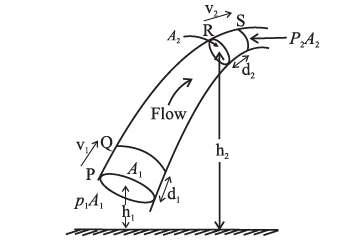
The fluid enters the system at point 1 through a surface of cross section A1, at speed v1. The point 1 lies at a height h1 with respect to an arbitrary reference level y = 0, and the local pressure there is p,. The fluid leaves the system at point 2 where the corresponding quantities are A2, v2, h2 and p2.
Consider a small fluid element, of volume ΔV and mass Δm=ρΔV, that enters at point 1 and leaves at point 2 during small time interval Δt. In the absence of internal fluid friction, it can be shown that the work done on the fluid element by the surrounding fluid is
ΔW: (p1-p2) ΔV
This is sometimes called the pressure energy.
During Δt, the changes in the kinetic energy and potential energy are
ΔKE =\frac{1}{2}Δm(v_2^2-v_1^2)=\frac{1}{2}ρΔV(v_2^2-v_1^2)
ΔPE =Δmg(h_2-h_1)=ρΔVg(h_2-h_1)
Since ΔW is the work done by a non-conservative force,
ΔW = ΔKE + ΔPE
(p1-p2) ΔV = \frac{1}{2}ρΔV(v_2^2-v_1^2)\)+ρΔVg(h_2-h_1)\) ….. (1)
∴ p1-p2 = \frac{1}{2}ρ(v_2^2-v_1^2)\)+ρg(h_2-h_1)\)
∴ p_1+\frac{1}{2}ρv_1^2+ρgh_1= p_2+\frac{1}{2}ρv_2^2+ρgh_2
Or p+\frac{1}{2}ρv^2+ρgh = constant ….. (2)
This is known as Bernoulli's equation.
| Note that in writing ΔW = ΔKE + ΔPE we have assumed principle of conservation of energy.
Dimensionally, pressure is energy per unit volume. Both terms on the right side of Eq. (2) also have the same dimensions. Hence, the term (p1-p2) is often referred to as pressure energy per unit volume or pressure head. The first term on the right, \frac{1}{2}p(v_2^2-v_1^2) , is called the velocity head and the second term,ρg(h_2-h_1) , is called the potential head. |
Limitations of Bernoulli’s principle : Bernoulli’s principle and his equation for fluid flow is valid only for an ideal fluid, i.e.,
- It is incompressible and non-viscous, so that the density remains constant throughout a flow tube and there is no viscous drag which results in energy dissipation or loss.
- It is a streamline flow.
Applications of Bernoulli's principle :
Venturi meter: It is a horizontal constricted tube that is used to measure flow speed in a gas.
Atomizer ; It is a hydraulic device used for spraying insecticide, paint, air perfume, etc.
Aerofoil; The aerofoil shape of the wings of an aircraft produces aerodynamic lift.
Bunsen’s burner ; Bernoulli effect is used to admit air into the burner to produce an oxidising flame.
Law of efflux (Torricelli’s theorem) : The Speed of efflux for an open tank through an orifice at a depth h below the liquid surface is equal to the speed acquired by a body falling freely through a vertical distance h
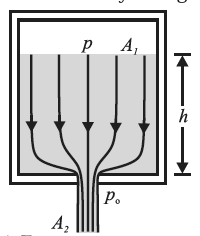
Consider a tank with cross—sectional area A1 holding a static liquid of density r. The tank discharges through an opening (of cross-sectional area A2) in the side wall at a depth h below the surface of the liquid. The flow speed at which the liquid leaves the tank is called the speed of efflux.
The pressure at point 2 it is the atmospheric Pressure po. Let the pressure of the air above the liquid at point 1 be p We assume that the tank is large in cross section compared to the opening (A1 >> A2), so that the upper surface of the liquid will drop very slowly. That is we may regard the liquid surface to be approximately at rest (v1» 0) Bernoulli's equation, in usual notation, states
∴ p_1+\frac{1}{2}ρv_1^2+ρgy_1= p_2+\frac{1}{2}ρv_2^2+ρgy_2
Substituting p1 = p, p2 = po, v1» 0 and y1-y2=h
v_2^2=2\frac{p-p_0}{ρ}+2gh
If the tank is open to the atmosphere, then p = P0,
v=\sqrt{2gh} , which is the law of efflux.
Venturi meter : ventury tube is used to measure the speed of flow of a fluid in a tube. It has a constriction in the tube. As the fluid passes through the constriction, its speed increases in accordance with the equation of continuity. The pressure thus decreases as required by the Bernoulli equation.
The constricted part of the tube is called the throat. Although a Venturi meter can be used for a gas, they are most commonly used for liquids. As the fluid passes through the throat, the higher speed results in lower pressure at point 2 than at point 1.
This pressure difference is measured from the difference in height h of the liquid levels in the U—tube manometer containing a liquid of density ρm (Fig). The following treatment is limited to an incompressible fluid.
Consider a horizontal constricted tube.
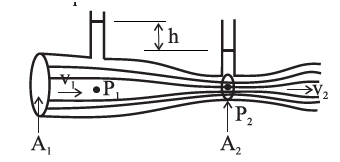
Let A1 and A2 be the cross-sectional areas at points P1 and P2, respectively.
Let v1 and v2 be the corresponding flow speeds.
ρ is the density of the fluid in the pipeline.
By the equation of continuity,
A1v1 = A2v2 ... (1)
v2/ v1 = A1/A2 > 1 (…A1>A2)
Therefore, the speed of the liquid increases as it passes through the constriction. Since the meter is assumed to be horizontal, from Bernoulli’s equation we get,
p_1+\frac{1}{2}ρv_1^2 = p_2+\frac{1}{2}ρv_2^2
∴ p_1+\frac{1}{2}ρv_1^2 = p_2+\frac{1}{2}ρv_1^2\frac{A_1^2}{A_2^2} ……..putting value of v2 from Eq. (1)
∴ p_1-p_2=\frac{1}{2}ρv_1^2\left[\frac{A_1}{A_2}-1\right] ........(2)
∴v_1^2=\sqrt{{\frac{2ρ_mgh}{ρ\left[\frac{A_1}{A_2}-1\right]}}} ........(3)
Equation (3) gives the flow speed of an incompressible fluid in the pipeline. The flow rates of practical interest are the mass and volume flow rates through the meter.
Volume flow rate = A1v1
And
Mass flow rate = density X volume flow rate = ρA1v1
Q. Explain aerodynamic lift on the wings of an aeroplane. OR
Explain why the upper surface of the wings of an aeroplane is made convex and the lower surface concave. (2 marks)
Ans. An aeroplane wing has a special characteristic aerodynamic shape called an aerofoil. An aerofoil is convex on the top and slightly concave on the bottom. Its leading edge is well rounded while the trailing edge is sharp. As an aeroplane moves through air, the aerofoil shape makes the air moving over the top and along the bottom of a wing in a certain way.
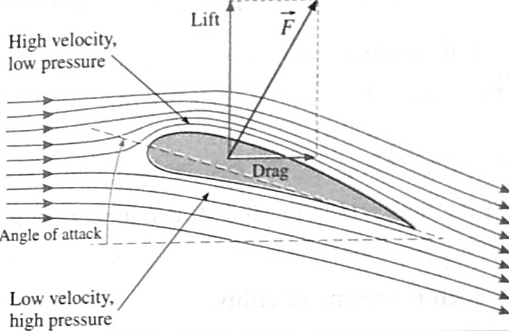
When an aeroplane runs on a runway, due to aerodynamic shape of its wings, the streamlines of air are crowded above the wings compared to those below the wings.
- Thus, the air above the wings moves faster than that below the wings.
- According to the Bernoulli’s principle, the pressure above the wings decreases and that below the wings increases.
- Due to this pressure difference, an upward force called the dynamic lift acts on the bottom of the wings of a plane.
- When this force becomes greater than the weight of aeroplane, the aeroplane takes off.
For an aeroplane to stay in level flight, the lift is equal in magnitude and opposite in direction to the force of gravity.
For an airborne aeroplane to get to the ground, the direction of F must be reversed. Then, the upper surface should be more concave than the lower surface such that air above the wing travels slower than the air below it, decreasing the air pressure below the wing. This is achieved by small flaps, called ailerons attached at the trailing end of each wing.
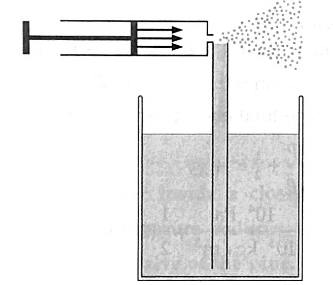
Working of an atomizer : An atomizer is a device which entraps or entrains liquid droplets in a flowing gas. It’s working is based on Bernoulli’s principle. A squeeze bulb or a pump is used to create a jet of air over an open tube dipped into a liquid. By Bernoulli's principle, the high-velocity air stream creates low pressure at the open end of the tube. This causes the liquid to rise in the tube. The liquid is then dispersed into a fine spray of droplets. This type of system is used in a perfume bottle, a paint sprayer, insect and perfume sprays and an automobile carburetor.
Blowing off of roofs by stormy wind: A cyclonic high wind blowing over a roof creates a low pressure above it, in accordance with Bernoulli's principle.
- The pressure below the roof is equal to the atmospheric pressure which is now greater than the pressure above the roof.
- This pressure difference causes an aerodynamic lift that lifts the roof up.
- Once the roof is lifted up, it blows off in the direction of the wind.
- Wind speeds in a tornado may be much higher and thus create much greater pressure differences. Sometimes, wooden houses hit by a tornado explode
| << Previous Part |
Useful links :
| Main Page : - Maharashtra Board Class 12-Physics - All chapters notes, solutions, videos, test, pdf.
Books : MSBSHSE -Class 12th Science Text Books – Chapter wise PDF for download Previous Chapter :Chapter-1-Rotational Dynamics - Online Notes Next Chapter :Chapter-3-Kinetic Theory of Gases and radiation -Online Notes |