Parallel lines and Transversal
Based on Maharashtra Board Class 8 Mathematics Chapter 2
Theory
- Parallel Lines
- Transversal
- Angles made by Transversal
- Corresponding angles
- Interior angles
- Alternate angles
- Construction of parallel lines
Parallel lines : The lines which lie in the same plane and do not intersect each other are called parallel lines.
In the fig. lines l and m are parallel lines. Symbolically, we can write line l || line m
Transversal : If a line intersects two or more given lines in two or more distinct points then the line is called a transversal of those two or more lines.
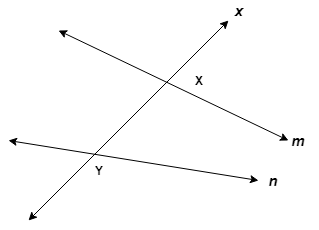
In the figure, line x intersects lines m and n in two distinct points 'X' and 'Y' respectively.
line x transversal of lines m and n.
Angle made by a transversal :
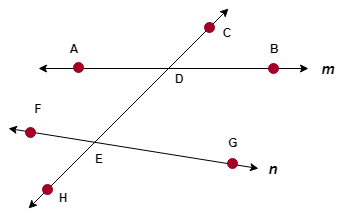
In the fig.
Line CH is transversal of lines AB and FG intersect at point D and point E.
At point D four angles formed namely ∠CDA, ∠CDB ∠ADE ∠BDE
At point E four angles formed namely ∠DEF, ∠DEG ∠FEH ∠GEH
Hence there are 8 angles in all. Each of these angle have one arm on transversal and other is on one of the given lines.
These angles are grouped in different pairs of angles as:
Corresponding angles : If the arms on the transversal of a pair of angles are in the same direction ( Ex. arm CD and arm DE ) and other arms are on the same side of transversal, (ex. arm DA and arm EF) then it is called a pair of Corresponding angles.
In the fig. there are four pairs of corresponding angles
 |
| (i) ∠CDA, and ∠DEF, (ii) ∠CDB and ∠DEG, (iii) ∠HEF and ∠EDA, ( iv) ∠HEG and ∠EDB |
Interior angles : A pair of angles which are on the same side of the transversal and inside the given lines is called a pair of interior angles.
 |
(i) ∠ADE, and ∠DEF
(ii) ∠BDE and ∠DEG |
Alternate angles : A pair of angles which are on the opposite sides of transversal and their arms on the transversal show opposite directions is called a pair of alternate angles.
In the figure there are two pairs of Interior alternate angles and two pairs of Exterior alternate angles.
 |
Interior alternate angles :
(i) ∠ADE, and ∠DEG (ii) ∠BDE and ∠DEF Exterior alternate angles (i) ∠CDB, and ∠FEH (ii) ∠CDA and ∠GEH |
Q-1. In the adjoining figure, each angle is shown by a letter. Fill in the boxes with the help of the figure.
Corresponding angles :
(1) ∠p and ___ (2) ∠q and ___ (3) ∠r and ___ (4) ∠s and ___
Interior alternate angles :
(1) ∠s and ___ (2) ∠w and ___
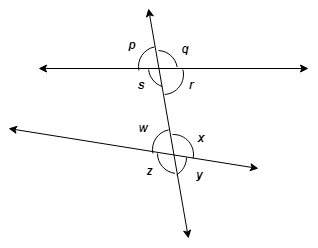
Sol: Corresponding angles : (1) ∠p and ∠w (2) ∠q and ∠x (3) ∠r and ∠y (4) ∠s and ∠z Interior alternate angles : (1) ∠s and ∠x (2) ∠w and ∠r
Q-2. Observe the angles shown in the figure and write the following pairs of angles.
(1) Interior alternate angles
(2) Corresponding angles
(3) Interior angles
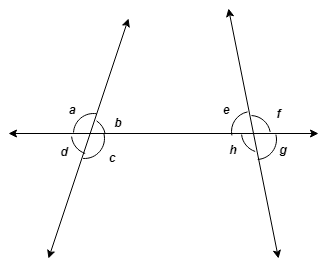
Sol: (1) Interior alternate angles: (1) ∠c and ∠e (2) ∠b and ∠h (2) Corresponding angles :(1) ∠a and ∠e (2) ∠d and ∠h (3) ∠b and ∠f (4) ∠c and ∠g (3) Interior angles : (1) ∠b and ∠e (2) ∠c and ∠h
(1) Property of corresponding angles:
Each pair of corresponding angles formed by two parallel lines and their transversals is of congurent angle.
 |
In the figure line AB || line CD, line EH is transversal
Corresponding angles : (ii) ∠EFB ≅ ∠FGD (iii) ∠EFA ≅ ∠FGC (iv) ∠HGD ≅ ∠GFB (iv) ∠HGC ≅ ∠GFA |
(1) Property of alternate angles:
Each pair of alternate angles formed by two parallel lines and their transversal is congruent angles
 |
In the figure line AB || line CD, line EH is transversal
Interior alternate angles : (ii) ∠AFG ≅ ∠FGD (ii) ∠BFG ≅ ∠FGC Exterior alternate angles : (iv) ∠EFB ≅ ∠CGH (iv) ∠EFA ≅ ∠HGD |
(1) Property of Interior angles:
Each pair of interior angles formed by two parallel lines and their transversal is of supplementary angles.
 |
In the figure line AB || line CD, line EH is transversal
Interior angles : (i) m∠AFG + m∠FGC = 180° (ii) m∠BFG + m∠FGD = 180°
|
| When two parallel lines intersected by a transversal, the angles formed in each pair of
(i) Corresponding angles are congruent (ii) Alternate angles are congruent (iii) Interior angles are supplementary (180°) |
| If a transversal intersects two coplanar lines and a pair of
(i) Corresponding angles is congruent then the lines are parallel (ii) Alternate angles is congruent then the lines are parallel (iii) Interior angles are supplementary (180°) then the lines are parallel |
Q1. Choose the correct alternative
In the figure line m || line n, line p is transversal, then find x.
(A) 135° (B) 90° (C) 45° (D) 40°
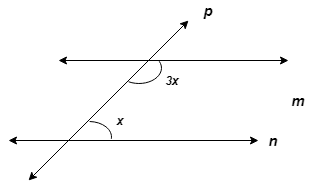 |
Answer Sol: 3x + x =180°…. (interior angles are supplementary) ∴ 4x = 180° ∴ x = 180° /4 = 45° Ans: C |
In the figure line a || line b, line l is transversal, then find x.
(A) 90° (B) 60° (C) 45° (D) 30°
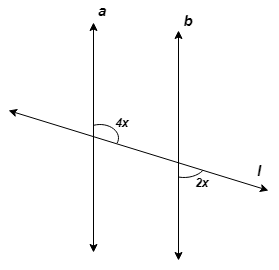 |
Answer Sol: 4x + 2x =180° ∴ 6x = 180° ∴ x = 180°/6 = 30° Ans: D |
Q2-In the given figure, line p || line q. Line t and line s are transversals. Find measures of ∠x and ∠y using the measures of angles given in the figure.

Answer Consider ∠a and ∠b as shown in the figure Line p || line q. Line t are transversals m∠a = 40° ……. (Corresponding angles ) m∠x + m∠a =180° ….. (angles in linear pair) ∴ m∠x + m∠40° =180° ∴ m∠x =180 – 40 = 140° Ans : m∠x = 140° |
Answer m∠b = 70° …(Vertically opposite angle) Line p || line q. Line s is the transversals. m∠y + m∠b =180° …..(Interior angles) ∴ m∠y + 70° =180° ∴ m∠y =180 – 70 = 110° Ans : m∠y = 110° |
Q3-In the given figure, line p || line q. Line m || line n. Find measures of ∠a, ∠b and ∠c using the measures of angles given in the figure. Justify your answer.
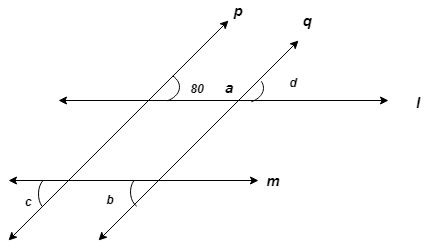
Sol: Consider ∠a as shown Line p || line q. Line l is the transversals. m∠d = 80° ……. (Corresponding angles ) m∠d + m∠a =180° ……. (angles in linear pair) ∴ 80 + m∠a =180° ∴ m∠a =180° – 80° = 100° Line l || line m. Line q is the transversals. ∠b ≅ ∠d ……. (Exterior alternate angles) m∠b = m∠d = 80° ∴ m∠b = 80° Line p || line q. Line m is the transversals. ∠c ≅ ∠b …….(Corresponding angles) m∠c = m∠b = 80° ∴ m∠c = 80° Ans : m∠a = 100° , m∠b = 80°, m∠c = 80°
Q4. In the adjoining figure, line a || line b. line l is a transversal. Find the measures of ∠ x, ∠ y, ∠ z using the given information
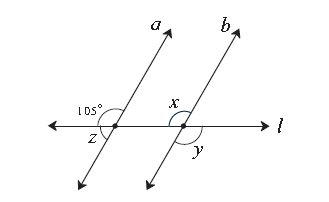
Sol: line a || line b. line l is a transversal m∠ x = 105° …….. (Corresponding angle) ∠ y ≅ ∠ x ……. (Vertically opposite angle) ∴ m∠ y = m∠ x ∴ m∠ y = 105° ∴ m∠ z + 105° = 180° …. (Angles in linear pair) ∴ m∠ z = 180° – 105° ∴ m∠ z = 75° Ans : m∠ x = 105°, m∠ y = 105° m∠ z = 75°
Q5*. In the adjoining figure, line p || line l || line q. Find ∠ x with the help of the measures given in the figure.
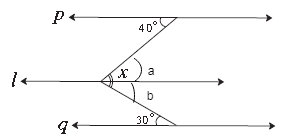 |
Answer Consider ∠a and ∠b as shown line p || line l and on the transversal m∠a = 40° ….(Alternate angles) line l || line q and on the transversal m∠b = 30° ….(Alternate angles) m∠x = m∠a + m∠b ∴ m∠x = 40° + 30° = 70° Ans: m∠x = 70° |
Draw a line parallel to the given line
|
Construction (I) : To draw a line parallel to the given line through a point outside the given line using set - square. Method I : Steps of the construction (4) Hold set - squares A and B. One edge of set - square A is close to point P. Draw a line along the edge of set - square B. |
 |
| Method II : Steps of construction (1) Draw line l. Take a point P outside the line. (2) Draw a seg PM ⊥ line l. (3) Take another point N on line l. (4) Draw seg NQ ⊥ line l. such that l(NQ) = l(MP). (5) The line m passing through points P and Q is parallel to the line l. |
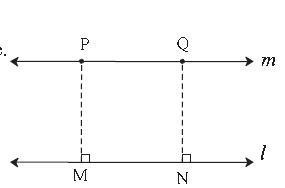 |
| Construction (II) : To draw a parallel line to a given line at a given distance. Method : Draw a line parallel to line l at a distance 2.5 cm. Steps of construction : (1) Draw line l. (2) Take two points A and B on the line l. (3) Draw perpendiculars to the line l from points A and B. (4) On the perpendicular lines take points P and Q at a distance of 2.5cm from A and B respectively. (5) Draw line PQ. (6) Line PQ is a line parallel to the line l at a distance 2.5cm |
 |