Rational & Irrational Numbers
Maharashtra Board Class 8- Mathematics - Chapter-1
Solution
| Exercise 1.1 |
Question 1.
Show the following numbers on a number line. Draw a separate number line for each example.
(1) 3/2, 5/2 , - 3/2
\(\frac{3}{2}=1\frac{1}{2}=1+\frac{1}{2}\) \(\frac{5}{2}=2\frac{1}{2}=2+\frac{1}{2}\) \(\frac{-3}{2}=-1\frac{1}{2}=-1-\frac{1}{2}\) Here, the denominators of the given numbers is 2. Therefore we divide each unit distance into 2 equal parts. \(\frac{-3}{2}\) is the number to the left of 0 And at the same distance, \(\frac{3}{2}\) is on the right of 0. 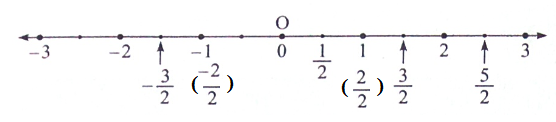
(2) 7/5 ,-2/5 , -4/5
Here \(\frac{7}{5}=1+\frac{2}{5}\) , \(\frac{7}{5}\) is at \(\frac{2}{5}\)th distance after 1 on the right side of zero Here, we divide each unit distance into 5 equal parts. 
(3) -5/8 , 11/8
Here \(\frac{11}{8}=1+\frac{3}{8}\) , \(\frac{11}{8}\) is at \(\frac{3}{8}\) th distance after 1 on the right side of zero Here, we divide each unit distance into 8 equal parts. 
(4) 13/10 , -17/10
\(\frac{13}{10}=1\frac{3}{10}=1+\frac{3}{10}\) \(\frac{-17}{10}=-1\frac{7}{10}=-1-\frac{7}{10}\) Here, we divide each unit distance into 10 equal parts. 
Question 2.
Observe the number line and answer the questions.

(1) Which number is indicated by point B?
The point B is at half distance of unit after -2 on the left side of zero. ∴ The number -10/4 or -5/2 is indicated by the point B.
(2) Which point indicates the number \(1\frac{3}{4}\)?
\(1\frac{3}{4}\) means \(\frac{3}{4}\) th distance of unit after 1 on the right side of zero. This number is indicated by the point C.
(3) State whether the statement, ‘the point D denotes the number 5/2 is true or false.
\(\frac{5}{2}=2\frac{1}{2}\) i.e. Half distance of unit after 2 on the right side of zero. The point D is at this place. ∴ The statement ‘the point D denotes the number 5/2 is true.
| Exercise 1.2 |
Question 1.
Compare the following numbers.
(1) -7, -2
If a and b are positive numbers such that a >b, then -a < -b Here, 7 > 2 ∴ -7 < -2 Ans. -7 < -2.
(2) 0, -9/5
On a number line, \(\frac{-9}{5}\) is to the left of zero ∴ \(\frac{-9}{5}\) < 0 i.e. 0 > \(\frac{-9}{5}\) Ans. 0 > \(\frac{-9}{5}\)
(3) 8/7 , 0
On a number line, 8/7 is to the right of zero ∴ \(\frac{8}{7}\) > 0 i.e. 0 < \(\frac{8}{7}\) Ans. 0 < 8/7
(4) -5/4 , 1/4
A negative number is always smaller than a positive number. ∴ -5/4 < 1/4 Ans. -5/4 < 1/4
(5) 40/29, 141/29
The denominator of the given rational numbers is the same. Let us compare their numerators 40 < 141 ∴ 40/29 < 141/29 Ans. 40/29 < 141/29
(6) -17/20 , -13/20
Because, the denominators are the same, let us compare the numerators of the given rational numbers. -17 < -13 ∴ -17/20 < -13/20 Ans. -17/20 < -13/20
(7) 15/12 , 7/16
\(\frac{15}{12}=\frac{15×16}{12×16}=\frac{240}{192}\) \(\frac{7}{16}=\frac{15×12}{16×12}=\frac{84}{192}\) Now \(\frac{240}{192}>\frac{84}{192}\) ∴ \(\frac{15}{12}>\frac{7}{16}\) Ans. \(\frac{15}{12}>\frac{7}{16}\)
(8) -25/8 , -9/4
\(\frac{-9}{4}=\frac{-9×2}{4×2}=\frac{-18}{8}\) Now -25<-18 ∴ \(\frac{-25}{8}<\frac{-9}{4}\) Ans. \(\frac{-25}{8}<\frac{-9}{4}\)
(9) 12/15 , 3/5
\(\frac{3}{5}=\frac{3×3}{5×3}=\frac{9}{15}\) ∴ \(\frac{12}{15}>\frac{3}{5}\) Ans. \(\frac{12}{15}>\frac{3}{5}\)
(10) -7/11 , -3/4
\(\frac{-7}{11}=\frac{-7×4}{11×4}=\frac{-28}{44}\) \(\frac{-3}{4}=\frac{-3×11}{4×11}=\frac{-33}{44}\) Now -33 < -28 ∴ \(\frac{-3}{4}<\frac{-7}{11}\) Ans. \(\frac{-3}{4}<\frac{-7}{11}\)
| Exercise 1.3 |
Question 1.
Write the following rational numbers in decimal form.
(1) 9/37
(2) 18/42

(3) 9/14

(4) -103/5
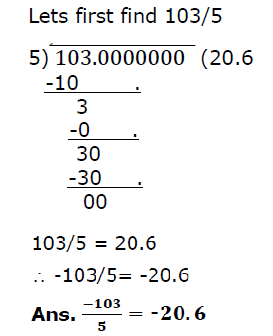
(5) – 11/13

| Exercise 1.4 |
(1) The number \(\sqrt{2}\) is shown on a number line. Steps are given to show \(\sqrt{3}\) on the number line using \(\sqrt{2}\) . Fill in the boxes properly and complete the activity.
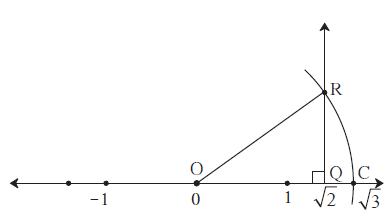
(i) The point Q on the number line shows the number \(\sqrt{2}\) (ii) A line perpendicular to the number line is drawn through the point Q. Point R is at unit distance from Q on the line l. (iii) Right angled Δ ORQ is obtained by drawing seg OR. l (OQ) = \(\sqrt{2}\) , l(QR) = 1 ∴ by Pythagoras theorem, [l(OR)]2 = [l(OQ)]2 + [l(QR)]2 = [ \(\sqrt{2}\) ]2 +[1]2 = [2] + [1] = [3] ∴ l(OR) = [ \(\sqrt{3}\)] Draw an arc with centre O and radius OR. Mark the point of intersection of the line and the arc as C. The point C shows the number \(\sqrt{3}\) .
(2). Show the number \(\sqrt{5}\) on the number line.
Draw a number line l, Take OP = 2 units. Draw a line m ⊥ line l through the point P Take a point Q on line m such that PQ = 1 unit. In right angled Δ OPQ, by Pythagoras theorem, [l (OQ)]2 = [l (OP)]2 + [l(PQ)]2 = (2)2+(1)2=4+ 1 =5. ∴ l(OQ) = \(\sqrt{5}\) With centre O and OQ as radius, draw an arc intersecting line l in the point R. OR = \(\sqrt{5}\) on the number line l. The point R represents the number \(\sqrt{5}\)
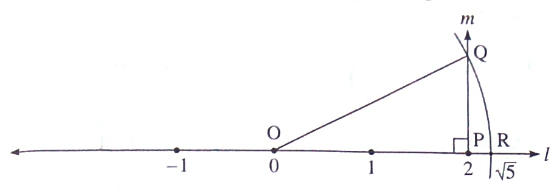
(3). Show the number on the number line.
Draw a number line l. Show the number \(\sqrt{5}\) on this number line Let the point R represent the number \(\sqrt{5}\) Draw seg RS ⊥ line l. Take RS = 1 unit. With centre O and radius OS draw an arc intersecting line l at the point T. l(OS)2 =( \(\sqrt{5}\) )2+(1)2 = 6 ∴ l(OS) = \(\sqrt{6}\) Point T will represent the number \(\sqrt{6}\) Draw seg TU ⊥ line l. Take TU = 1 unit. With centre O and radius OU draw an arc intersecting line l at the point V. l(OU)2 =( \(\sqrt{6}\) )2+(1)2 = 7 ∴ l(OU) = \(\sqrt{7}\) This point V will represent the number \(\sqrt{7}\)

Useful links :
| Main Page : - Maharashtra Board Class 8th Mathematics - All chapters notes, solutions, videos, test, pdf.
Next Chapter : Chapter 2- Parallel lines and transversals -online Solution |