उष्णतेचे मापन व परिणाम
इयत्ता-आठवी – सामान्य विज्ञान-पाठ -14- Maharashtra Board
स्वाध्याय प्रश्नोत्तरे
प्रश्न 1.( A) माझी जोडी कोणाशी?
| ‘अ’ गट | ‘ब’ गट |
| अ. निरोगी मानवी शरीराचे तापमान | i. 296 K |
| आ. पाण्याचा उत्कलन बिंदू | ii. 98.6 0F |
| इ. कक्ष तापमान | iii. 0 0C |
| ई. पाण्याचा गोठण बिंदू | iv. 212 0F |
(अ) निरोगी मानवी शरीराचे तापमान : 98.6 °F
(आ) पाण्याचा उत्कलन बिंदू : 212 °F
(इ) कक्ष तापमान : 296 K
(ई) पाण्याचा गोठण बिंदू : 0 °C.
(B) कोण खरं बोलतोय?
(अ) पदार्थाचे तापमान ज्यूलमध्ये मोजतात.
चूक. (पदार्थाचे तापमान C अथवा F अथवा K मध्ये मोजतात.)
(आ) उष्णता उष्ण वस्तूकडून थंड वस्तूकडे वाहते.
बरोबर.
(इ) उष्णतेचे एकक ज्यूल आहे.
बरोबर.
(ई) उष्णता दिल्याने वस्तू आकुंचन पावतात.
चूक. (सामान्यतः उष्णता दिल्याने वस्तू प्रसरण पावतात. याला काही अपवाद आहेत.)
(उ) स्थायूचे अणू स्वतंत्र असतात.
चूक. (स्थायूचे अणू त्यांच्यामधील परस्पर बलाने बांधलेले असतात.)
(ऊ) उष्ण वस्तूच्या अणूंची सरासरी गतिज ऊर्जा थंड वस्तूंच्या अणूंच्या सरासरी गतिज ऊर्जेपेक्षा कमी असते.
चूक. (उष्ण वस्तूच्या अणूंची सरासरी गतिज ऊर्जा थंड वस्तूच्या अणूंच्या सरासरी गतिज ऊर्जेपेक्षा जास्त असते.)
(C) शोधाल तर सापडेल.
(अ) तापमापी हे उपकरण .......... मोजण्यास वापरतात.
तापमापी हे उपकरण तापमान मोजण्यास वापरतात.
(आ) उष्णता मोजण्यास .......... हे उपकरण वापरतात.
उष्णता मोजण्यास कॅलरीमापी हे उपकरण वापरतात.
(इ) तापमान हे वस्तूतील अणूंच्या .......... गतिज ऊर्जेचे प्रमाण असते.
तापमान हे वस्तूतील अणूंच्या सरासरी गतिज ऊर्जेचे प्रमाण असते.
(ई) एखाद्या वस्तूतील उष्णता ही त्यातील अणूंच्या .......... गतिज ऊर्जेचे प्रमाण असते.
एखाद्या वस्तूतील उष्णता ही त्यातील अणूंच्या एकूण गतिज ऊर्जेचे प्रमाण असते.
प्रश्न 2. निशिगंधाने चहा बनविण्यासाठी चहाचे घटक टाकून भांडे सौरचुलीत ठेवले. शिवानीने तसेच भांडे गॅसवर ठेवले. कोणाचा चहा लवकर तयार होईल व का?
शिवानीचा चहा लवकर तयार होईल. कारण, ठरावीक कालावधीत गॅसकडून भांड्याला मिळणारी उष्णता ही त्याच कालावधीत सौर चुलीकडून भांड्याला मिळणाऱ्या उष्णतेपेक्षा बरीच जास्त असते.
प्रश्न 3. थोडक्यात उत्तरे द्या.
(अ) वैद्यकीय तापमापीचे वर्णन करा. त्यात व प्रयोगशाळेत वापरल्या जाणाऱ्या तापमापीत कोणता फरक असतो?
वैद्यकीय तापमापी अथवा ज्वरमापी : पाऱ्याला उष्णता दिली असता त्याचे समप्रमाणात प्रसरण होते, या गुणधर्माचा उपयोग करून हे उपकरण तयार केलेले आहे.
रचना :
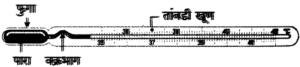
- वैद्यकीय तापमापी अथवा ज्वरमापी ही जाड काचेची, समान अंतर्व्यासाची एक केशनलिका असते.
- तिच्या एका टोकाशी पातळ काच असलेला फुगा असतो. त्यापुढील नळीच्या एका बाजूला बहिर्वक्र भिंगाचा आकार दिलेला असतो. त्यामुळे तापमान पाहणे सोपे जाते.
- वैदयकीय तापमापी अथवा ज्वरमापी फुग्यापासून निघालेल्या केशनलिकेचा भाग काही अंतरावर किंचित वक्र आणि चिंचोळा केलेला असतो.
- त्यामुळे ज्वरमापीत वर चढलेला पारा (अथवा अल्कोहोल) तापमान कमी झाल्यावर आपोआप फुग्यात परत येत नाही.
- या ज्वरमापीवर साधारणतः 35 °C ते 42C (किंवा 95° ते 108 °F) पर्यंत तापमानाच्या खुणा केलेल्या असतात.
- 37 °C (98.6 °F) या अंकावर एक तांबडी खूण (बाण) केलेली असते. ती निरोगी माणसाच्या शरीराचे तापमान दर्शवते.
ज्वरमापीचा उपयोग आपल्या शरीराचे तापमान मोजण्यासाठी होतो. प्रयोगशाळेतील तापमापीला ज्वरमापीप्रमाणे वक्रभाग नसतो व त्याची तापमान मापनाची मर्यादा ज्वरमापीच्या मानाने जास्त असते.
(आ) उष्णता व तापमानात काय फरक आहे? त्यांची एकके कोणती?
| उष्णता | तापमान |
| पदार्थातील अणूंची एकूण गतिज ऊर्जा ही पदार्थातील उष्णतेची मापक असते. | वस्तूतील अणूंची सरासरी गतिज ऊर्जा ही त्या वस्तूच्या तापमानाचे मापक असते. |
| उष्णता ही अधिक तापमान असलेल्या वस्तुकडून कमी तापमान असलल्या वस्तूकडे प्रवाहित होणारी ऊर्जा होय. | तापमान ही राशी उष्णतेच्या स्थानांतराची दिशा ठरवते. एखाद्या वस्तूचे तापमान हे ती वस्तू किती उष्ण अथवा थंड आहे हे दर्शवते, |
- उष्णतेचे SI मधील एकक Joule (ज्यूल) व CGS मधील एकक Calorie (कॅलरी) हे आहे. उष्णता ही ऊर्जेचे एक स्वरूप असल्याने ती अर्ग या एककातही व्यक्त करता येते.
- तापमानाचे SI एकक केल्व्हीन (K) आहे. तापमान C (अंश सेल्सिअस) व F (अंश फॅरेनहाईट) मध्येही व्यक्त करतात.
(इ) कॅलरीमापीची रचना आकृतीसह समजवा.
वस्तूतील उष्णता मोजण्यासाठी कॅलरीमापी हे उपकरण वापरले जाते. या उपकरणाद्वारे एखाद्या रासायनिक किंवा भौतिक प्रक्रियेमध्ये बाहेर पडणाऱ्या किंवा शोषित होणाऱ्या उष्णतेचे मापन करू शकतो.
कॅलरीमापीची रचना : आकृती मध्ये कॅलरीमापीची रचना दाखवली आहे.
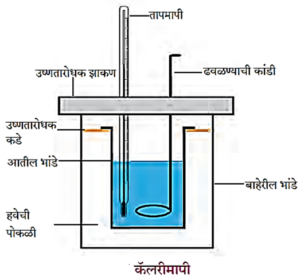
- थर्मास फ्लास्कप्रमाणे कॅलरीमापीत आत व बाहेर अशी दोन भांडी असतात. आतील भांडे तांब्याचे असते, तर बाहेरील भांडे लाकडाचे असते.
- बाहेरील भांड्यावर उष्णतारोधक झाकण असते. त्याला दोन भोके असतात. त्यांचा उपयोग करून कॅलरीमापीत तापमान मोजण्यासाठी एक तापमापी व द्रव ढवळण्यासाठी एक कांडी बसवलेली असते.
- तांब्याच्या भांड्याचे आतील व बाहेरील पृष्ठभाग चकचकीत केलेले असतात. त्यामुळे कॅलरीमापी व बाहेरील वातावरण यांमध्ये प्रारणामुळे होणारी उष्णतेची देवाण-घेवाण कमीत कमी होते.
- कॅलरीमापीतील वस्तू सभोवतालपासून औष्णिकदृष्ट्या अलिप्त ठेवतात, म्हणजेच कॅलरीमापीमधील वस्तूंतील उष्णता आतून बाहेर जाऊ शकत नाही, तसेच उष्णता बाहेरून आत येऊ शकत नाही.
(ई) रेल्वेच्या रुळांत ठराविक अंतरावर फट का ठेवली जाते हे स्पष्ट करा.
वातावरणाचे तापमान वाढल्यावर रेल्वेच्या रुळांची लांबी वाढते. तसेच रूळ व धावत्या गाडीची चाके यांच्यामधील घर्षणामुळे रुळांचे तापमान वाढते व परिणामी रुळांची लांबी वाढते. रुळांत ठरावीक अंतरावर फट न ठेवल्यास ते प्रसरणामुळे वाकडे होतील व त्यामुळे अपघात होतील. म्हणून रेल्वेच्या रुळांत ठरावीक अंतरावर फट ठेवली जाते.
(उ) वायूचा व द्रवाचा प्रसरणांक म्हणजे काय हे सूत्रांद्वारे स्पष्ट करा.
(i) वायूचा प्रसरणांक : वायूला ठरावीक आकारमान नसल्याने तो भांड्यात बंदिस्त करावा लागतो. दाब कायम ठेवून तापमान वाढवल्यास वायू व भांडे या दोन्हींचे प्रसरण होते.
समजा, एका ठरावीक वस्तुमानाच्या वायूला दाब कायम ठेवून उष्णता दिल्यास त्याचे तापमान ΔT (अतिशय कमी, very small) ने वाढवल्यास त्याचे आकारमान V1 पासून V2 पर्यंत वाढते. प्रयोगांवरून असे दिसते की, आकारमानांतील वाढ, V2 - V1 ही V1 व ΔT च्या अनुपातात असते,
म्हणजेच (V2 - V1) ∝ V1ΔT
∴ V2 - V1 = β V1ΔT
येथे β हा वायूचा स्थिर दाब प्रसरणांक होय.
β = \(\frac{V_2-V_1}{V_1ΔT}\), हा 1/°C मध्ये व्यक्त करतात.
β म्हणजे स्थिर दाबास एकक आकारमानाच्या वायूचे तापमान एक अंशाने (तापमानाच्या एककाने) वाढवल्यावर त्याच्या आकारमानात होणारी वाढ होय. वरील सूत्रावरून,
V2 = V1 + β V1ΔT = V1 (1 + βΔT).
(ii) द्रवाचा प्रसरणांक : द्रव भांड्यात ठेवतात. द्रवाला उष्णता देताना द्रवाचे तसेच भांड्याचे प्रसरण होते. सामान्यतः भांड्याचे प्रसरण द्रवाच्या प्रसरणापेक्षा खूपच कमी असल्याने ते विचारात घेत नाहीत.
समजा, एका द्रवाचे तापमान ΔT (अतिशय कमी, very small) ने वाढवल्यास त्याचे आकारमान V1 पासून V2 पर्यंत वाढते. प्रयोगांवरून असे दिसते की, आकारमानांतील वाढ, V2 - V1 ही V1 व ΔT च्या अनुपातात असते,
म्हणजेच (V2 - V1) ∝ V1ΔT
∴ V2 - V1 = β V1ΔT
येथे β हा द्रवाचा प्रसरणांक होय.
β = \(\frac{V_2-V_1}{V_1ΔT}\), हा 1/°C मध्ये व्यक्त करतात.
β म्हणजे एकक आकारमानाच्या द्रवाचे तापमान एक अंशाने (तापमानाच्या एककाने) वाढवल्यावर त्याच्या आकारमानात होणारी वाढ होय.
वरील सूत्रावरून,
V2 = V1 + β V1ΔT = V1 (1 + βΔT).
प्रश्न 4. खालील उदाहरणे सोडवा.
(अ) फॅरेनहाईट एककातील तापमान किती असल्यास ते सेल्सिअस एककातील तापमानाच्या दुप्पट असेल?
दिलेले : F = 2C .: C = F/2, F = ?
\(\frac{F-32}{9}=\frac{c}{5}=\frac{F/2}{5}=\frac{F}{10}\)
∴ F – 32 = \(\frac{9F}{10}\)
∴ 10F – 320 = 9F
∴ F = 320
फॅरेनहाईट एककातील तापमान = 320 °F.
(आ) एक पूल 20 m लांबीच्या लोखंडाच्या सळईने तयार केला आहे. तापमान 18 0C असताना दोन सळयांत 4 cm अंतर आहे. किती तापमानापर्यंत तो पूल सुस्थितीत राहील?
दिलेले : l1 = 20 m, l2 – l1 = 0.4 cm = 4 × 10-3 m. T1 = 18°C, λ = 11.5 × 10-6/°C, T2 =?
l2 – l1 = λl1ΔΤ
4 × 10-3 = (11.5 × 10-6) × 20 × ΔΤ
∴ ΔΤ = \(\frac{4×10^{-3}}{11.5×10^{-6}×20}=\frac{400}{23}\) = सुमारे 17.39°C
आता ΔT = T2 - T1 ∴ T2 = T1 + ΔT
∴ T2 = 18 + 17.39 = 35.39 ℃.
तो पूल 35.39 ℃ तापमानापर्यंत सुस्थितीत राहील.
(इ) आयफेल टॉवरची उंची 15 0C वर 324 m असल्यास, व तो टॉवर लोखंडाचा असल्यास, 30 0C ला त्याची उंची किती cm ने वाढेल?
दिलेले: l1 = 324 m. T1 = 15°C, T2 = 30 0C, λ = 11.5 × 10-6/℃. l2 – l1 = ?
आयफेल टॉवरच्या उंचीतील वाढ,
l2 – l1 = λl1ΔΤ = 11.5 × 10-6 × 324 × (30 - 15)
= 11.5 × 324 × 15 × 10-6
= 55890 × 10-6
= 5.589 × 10-2 × 102 cm
= 5.589 cm = सुमारे 5.6 cm.
(ई) अ व ब पदार्थांचा विशिष्ट उष्मा क्रमशः c व 2c आहे. अ ला Q व ब ला 4Q एवढी उष्णता दिली गेल्यास त्यांच्या तापमानात समान बदल होतो. जर अ चे वस्तुमान m असेल तर ब चे वस्तुमान किती असेल?
दिलेले : c(अ) = c, c(ब) = 2c, Q(अ )= Q, Q(ब) = 4Q. ΔT समान, m(अ) = m, m(ब) = ?
Q = mcΔT ∴ ΔT = \(\frac{Q}{mc}\)
ΔT समान असल्यामुळे,
\(\frac{Q(अ)}{m(अ)c(अ)}\) = \(\frac{Q(ब)}{m(ब)c(ब)}\)
\(\frac{Q}{mc}\) = \(\frac{4Q}{m(ब)2c}\)
\(\frac{1}{m}\) = \(\frac{2}{m(ब)}\)
∴m(ब) = 2m
∴ ब चे वस्तुमान m(ब) = 2m.
(उ) एक 3 kg वस्तु मानाची वस्तू 600 कॅलरी ऊर्जा प्राप्त करते तेव्हा तिचे तापमान 10 0C पासून 70 0C पर्यंत वाढते. वस्तूच्या पदार्थाचा विशिष्ट उष्मा किती आहे?
दिलेले : m = 3 kg = 3000 g. Q = 600 cal, ΔT = 70 ℃ - 10 ℃ = 60 ℃, c = ?
Q = mcΔT
∴ वस्तूच्या पदार्थाचा विशिष्ट उष्मा,
c = \(\frac{Q}{mΔT}\) = \(\frac{600}{3000×60}\) = \(\frac{10}{3000}\) cal/(g·℃)
= 3.333 × 10-3 cal/(g·℃).
Click on link to get PDF from store
PDF : MSBSHSE-इयत्ता-आठवी – सामान्य विज्ञान-पाठ-14-उष्णतेचे मापन व परिणाम - नोट्स
PDF : MSBSHSE-इयत्ता-आठवी – सामान्य विज्ञान-पाठ-14-उष्णतेचे मापन व परिणाम - स्वाध्याय प्रश्नोत्तरे
Useful links :
| Main Page : - Maharashtra Board इयत्ता-आठवी – सामान्य विज्ञान - All chapters notes, solutions, videos, test, pdf.
Previous Chapter : पाठ - 13 : रासायनिक बदल व रासायनिक बंध - Online Solutions Next Chapter : पाठ - 15 : ध्वनी - Online Solutions |
