Notes
|
Topics to be learn :
|
Motion of an object (a body): A body is said to be in motion if it changes its position with respect to its surroundings and at rest otherwise.
- To decide whether an object is in motion or not we consider whether it changes its position with respect to its surroundings or not. Example: If you are travelling by the bus and bus is running then, the person sitting next to you is not in motion with respect to you, but that person is in motion with respect to a person outside the bus.
- A body is said to be at rest when it does not change its position with respect to its surroundings. Example : A stationary train, A stone lying on a hill
Distance : ‘Distance’ is the length of the actual path followed by an object in motion while going from one point to another.
- Its SI unit is the metre (m) and CGS unit is the centimetre (cm).
- Distance has magnitude, but not direction. It is a scalar quantity.
Displacement : Displacement is the shortest distance from the initial point to the final point of movement of a body.
- Its SI unit is the metre (m) and CGS unit is the centimetre (cm). same as those of distance.
- Displacement has magnitude and direction. It is a vector quantity.
Remember :
|
Speed and velocity :
Speed : Speed is the distance covered by a body in unit time.
Speed = total distance covered / total time taken
- Its SI unit is the metre/second (m/s) and CGS unit is the centimetre/second (cm/s).
- Speed has magnitude, but not direction. It is a scalar quantity.
Speed = distance/time.
∴ Distance = speed x time.
Average speed : It is the ratio of the total distance covered by a body to the total time taken to do so.
If a body covers distance s1 in time t1 and then distance s2 in time t2 its average speed over the time (t1 + t2) is \(\frac{s_1+s-2}{t_1+t_2}\)
Remember :
|
Velocity : Velocity is the distance covered by a body in a given direction in unit time. Thus, it is the displacement in unit time or the rate at which displacement takes place with respect to time.
Velocity = displacement/time
- Its SI unit is the metre/second (m/s) and CGS unit is the centimetre/second (cm/s). same as those of speed.
- Velocity has both magnitude and direction. It is a vector quantity.
- When a body moves without a change of direction of motion, the magnitude of the velocity of the body equals the speed of the body.
- When there is a change in the direction of motion of a body as the body moves along a curve or follows a zigzag path, the speed of the body is greater than the magnitude of the velocity of the body.
The velocity of a body can be changed by,
- Changing the speed, keeping the direction of motion the same : When a body falls under gravity its speed increases, but its direction of motion remains the same.
- Changing the direction of motion, keeping the speed constant : When a body moves along a circular path, covering equal distances in small equal intervals of time, its direction of motion changes continuously but there is no change in its speed.
- Changing both the speed and the direction of motion of the body : When a body is projected obliquely in air, it moves along a curved path such that its speed as well as direction of motion change continuously,
Uniform and non-uniform linear motion : Uniform motion: Uniform motion is the motion in which a body covers equal distances in very small equal intervals of time. Examples : Nonuniform motion : Nonuniform motion is the motion in which a body covers unequal distances in equal intervals of time.
Acceleration :
Acceleration: Acceleration is the rate of change of velocity with respect to time.
Acceleration = \(\frac{\text{change in velocity}}{time}\)
If a body moves in a straight line, its acceleration, a =|(\frac{v-u}{t}\) , where u is the initial velocity of the body and v is the velocity of the body after time t. v is often called the final velocity.
- The SI unit of acceleration is m/s2 and CGS unit is cm/s2.
- Acceleration has both magnitude and direction. It is a vector quantity.
- If there are equal changes in the velocity of a body in very small equal intervals of time, the acceleration of the body is uniform, otherwise it is nonuniform.
Accelerated motion is the one in which a body’s velocity goes on changing with time. Positive acceleration : When the velocity of a body increases with time, its acceleration is positive. Negative acceleration : When the velocity of a body decreases with time, its acceleration is negative and is called deceleration or retardation. Zero acceleration : If the velocity is uniform, acceleration is zero.
Distance-time graph for uniform motion :
A distance-time graph : It is a graph of distance covered by a body from the starting point against time i.e., it gives the variation of distance with time.
- In this graph, time is taken along the X-axis and distance along the Y-axis.
Uses of a distance-time graph:
- To find the position of the body at any time in the given time interval
- To find the speed of the body at any time in the given time interval
- To find the average acceleration when speed at different times is found.
Distance Time Graph for Uniform Motion :
The following table shows the distances covered by a car in fixed time intervals.
A graph of distance against time :
Taking ‘time’ along the X-axis and ‘distance’ along the Y-axis is as shown below.
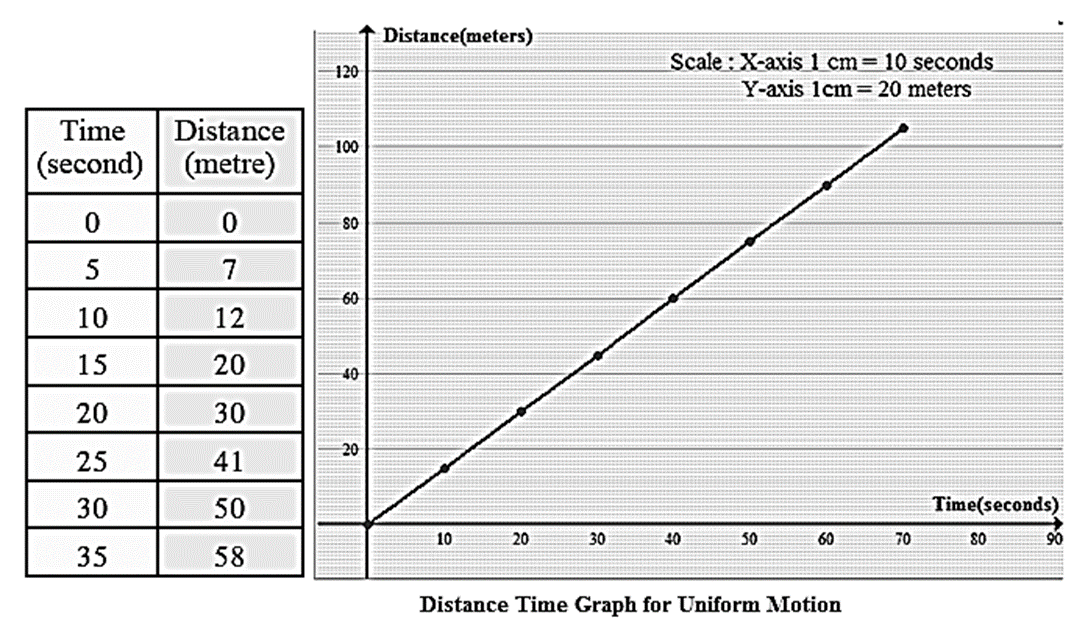
The graph between distance and time shows a straight line. It means an object in uniform motion covers equal distances in equal time intervals.
In the above graph, the slope of the straight line gives the speed of the car.
Distance Time Graph for nonuniform Motion :
Here, the distance changes non-uniformly with time.
| Time
(seconds) |
0 | 5 | 10 | 15 | 20 | 25 | 30 | 35 |
| Distance
(meters) |
0 | 7 | 12 | 20 | 30 | 41 | 50 | 58 |
Q. What difference do you see in the distance-time graphs for uniform and nonuniform motion?
A body is said to have nonuniform motion when it covers unequal distances in equal intervals of time. In this case, the speed of the body is not constant.
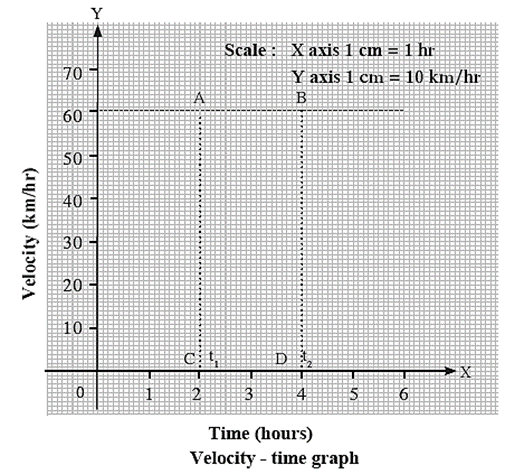
Velocity-time graph for uniform velocity : A train is moving with a uniform velocity of 60 km/hour for 5 hours. The velocity-time graph for this uniform motion is shown in figure Relation between the distance covered by the train between 2 and 4 hours and the area of a particular quadrangle in the graph : Distance covered by the train between 2 and 4 hours, s = vt = 60 km/h x (4 h – 2 h) = 120 km ….(1) From the graph : Area ABCD = 60 km/h x 2h = 120 km = s in eq. (1)
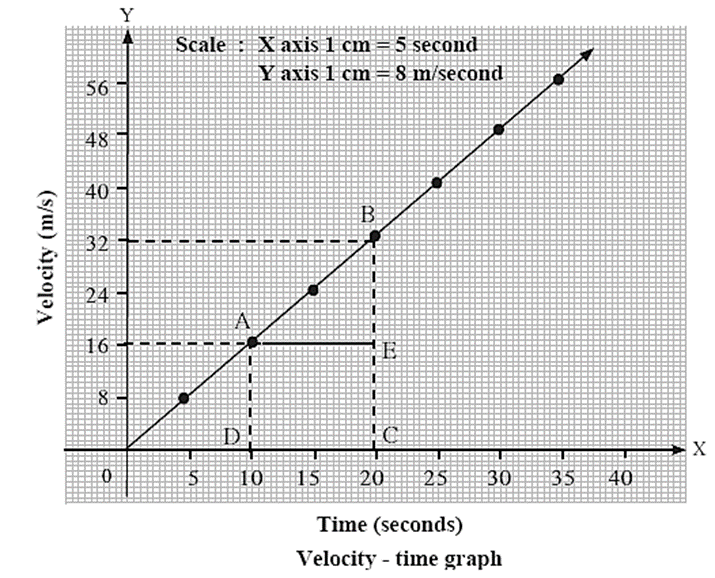
Velocity-time graph for uniform acceleration : The changes in the velocity of a car in specific time intervals are given in the following table. The velocity changes by 8 m/s in every 5 seconds. Displacement, s = average velocity x time = \(\frac{16+32}{2}m/s×(20-10)s\) = 24 m/s x 10 s = 240m ….(1) Also from graph, s = A([]DABC) = A([]DAEC) + A(ΔABE) =16 x 10 + ½ (32 - 16) x (20 -10) =160 m + 80 m = 240 m.
Time (seconds)
0
5
10
15
20
25
30
35
Velocity (m/s)
0
8
16
24
32
40
48
56
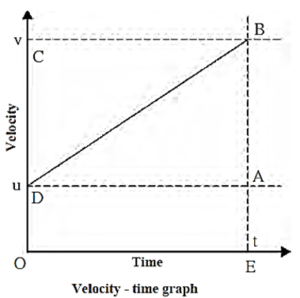
Equations of motion using graphical method For a body moving along a straight line with uniform acceleration a, the equations of motion relating u (initial velocity), v (velocity after time t), s (displacement in time t), a and t are Let us obtain these equations by the graphical method. Consider a body moving along a straight line with uniform acceleration a. Let u=initial velocity of the body (≠ 0), v = velocity of the body after time t, also called the final velocity and s = displacement of the body in time t. Fig. shows the corresponding velocity-time graph. D and B correspond to the initial and final positions of the body. (1) Velocity-time relation a = \(\frac{\text{change in velocity}}{time}=\frac{AB}{t}\) ∴ AB = at BE = BA + AE = BA + DO ∴ v = at + u ∴ v = u + at …(first kinematical equation) (2) Displacement-time relation Distance covered in time t= area enclosed within ODBE under velocity-time graph. s = area of quadrilateral ODBE = area of rectangle ODAE + area of triangle DAB =(OE x OD) + ½ (DA x AB) Now, OE = DA = t, OD = u and AB = at s = (t x u) + ½ (t x at) ∴ s = ut + ½ at2 …..(second kinematical equation) (3) Displacement-velocity relation s = area of trapezium ODBE = ½ (BE + OE) x OE Now, OD = u, BE = v and OE = t ∴ s = ½ (v + u) x t ...(1) Now a = \(\frac{v-u}{t}\) ∴ t = \(\frac{v-u}{a}\) ...(2) From Eqs. (1) and (2), we have, s = ½ (v + u)\((\frac{v-u}{a})\) ∴ 2as = v2 – u2 v2 = u2 + 2as ….. (third kinematical equation)
Uniform circular motion:
Uniform circular motion: When a body moves in a circular path with uniform speed, its motion is called uniform circular motion.
In this case, speed, v = \(\frac{circumference}{time}=\frac{2πr}{t}\) where r is the radius of the circular path and t is the time taken by the body to complete one revolution (periodic time).
Examples of uniform circular motion :
- Motion of the moon around the earth
- Motion of the electron around the nucleus of the hydrogen atom
- Motion of the blades of a fan (when the speed is not changed)
- Motion of a communication satellite (a geostationary satellite used for communication) around the earth.
Determining the direction of velocity in uniform circular motion: The direction of velocity of a particle performing uniform circular motion is along the tangent to the circle at the position of the particle, in the sense of motion of the particle.
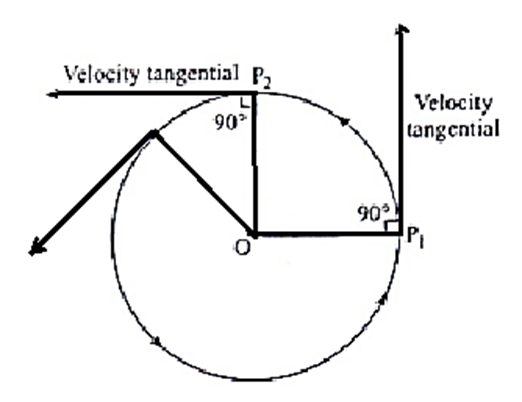
Newton’s first law of motion:
Newton’s first law of motion: An object continues to remain at rest or in a state of uniform motion along a straight line unless an external unbalanced force acts on it.
- This law explains the inertia of a body. All examples of inertia are examples of Newton’s first law of motion. Hence, this law is also called the law of inertia.
Force : Force is a physical quantity that changes the state of rest or of uniform motion of a body in a Straight line.
Unit force : A force which causes a unit mass to move with a unit acceleration is called a unit force.
- The effect of force applied to a body depends upon how much force we apply, i.e., the magnitude of the force and the direction in which the force is applied.
Effects of force : Force is an interaction between two objects :
Balanced and unbalanced force :
Balanced forces : When a rigid body acted upon by two forces is equal in magnitude, opposite in direction and having the same line of action. These forces are called balanced forces as their net effect on the body is zero.
- Example : A Book kept on a table is acted upon by two balanced forces : first the weight of the Book acting downward and second the upward force on the book due to the table. Their net effect on the book being zero, the book remains at rest.
Unbalanced force : A single force acting on a body is an unbalanced force. It produces acceleration in the body. If two or more forces act on a body such that their resultant is not zero, the resultant is an unbalanced force responsible for accelerating the body.
- Example : When a ball lying on the ground is hit with a bat, the ball is set in motion by the applied force.
Remember :
- If the force is removed completely when an object acquires a certain speed, the object will move with the velocity it has at the instant the force is removed.
- When a body exerts a force on another body, the other body, too, exerts an equal, in magnitude, and opposite, in direction, force on the first one at the same time.
- Forces always occur in pairs; an isolated single force does not exist in the universe.
| Know This :
Inertia : The tendency of a body to resist a change in its state of rest or state of motion is called inertia. Types of inertia : Inertia of rest :The intrinsic property of a body by virtue of which it cannot change its position of rest is called the inertia of rest.
Inertia of motion : The intrinsic property of a body by virtue of which it cannot change its state of motion is called the inertia of motion.
Inertia of direction : The intrinsic property of a body by virtue of which it cannot change its direction of motion is called the inertia of direction.
|
Newton’s second law of motion :
Newton’s second law of motion states that, the rate of change of momentum is directly proportional to the applied force and the change of momentum occurs in the direction of the force.
Momentum : Momentum is the product of mass and velocity of an object.
Momentum of a body (P) = mass of the body (m) x velocity of the body (v).
- It is a vector quantity. Its SI unit is kg-m/s and CGS unit is g-cm/s.
Q. When a bullet is fired from a gun, it pierces through a wooden plank, but the same bullet when thrown with hand hardly scratches it. Explain why ?
Equation of motion from Newton’s second law of motion : Let a constant force F act on a body of mass ‘m’. We assume that the motion of the body is along a straight line. Let ‘a’ be the acceleration produced by the force. Let u be the initial velocity of the body and ‘v’ its velocity after time t i.e. the final velocity. Initial momentum of the body = mu Final momentum of the body = mv Change in the momentum of the body = mu − mu Rate of change of momentum of the body =\(\frac{\text{change in the momentum of the body}}{\text{time interval}}\) = (mv−mu)/t = m(v—u)/t = ma ( Because a = (v−u)/t) Now, according to Newton’s second law of motion, rate of change of momentum a force ∴ ma ∝ F ∴ F = kma , where k is a constant of proportionality ….(1) By defining unit force as that force which produces unit acceleration in a unit mass, we have, F=1 unit. If m =1 unit and a = 1 unit 1 unit = k x 1 unit x 1 unit K = 1 Substituting k = 1 in Eq. (1), we get. ∴ F = ma Force = mass x acceleration This equation is known as the force equation or the equation of motion. Force is a vector quantity. Its SI unit is the newton (N) and CGS unit is the dyne. 1 N = 1 kg-m/s2, 1 dyne = 1 g.cm/s2
Newton’s third law of motion:
Every action force has an equal and opposite reaction force which acts simultaneously.
Explanation:
- When one object applies a force on another object, the latter object also simultaneously applies a force on the former object.
- The forces between two objects are always equal and opposite.
Law of conservation of momentum :
- When no external force acts on two interacting objects, their total momentum remains constant. It does not change.
- This law can also be stated as follows: When no external force acts on two objects in collision, the total momentum before the collision is equal to the total momentum after the collision.
Q. When a bullet is fired from a gun, the gun recoils. Explain why.