Rotational Dynamics
Maharashtra State Engineering Entrance Examination-Physics-Chapter-1
Notes-Part-2
Topics:
Moment of Inertia | Physical Significance of Moment of Inertia | Theorem of Parallel and Perpendicular Axes Radius of Gyration | Kinetic Energy of a Rotating Body | Torque Acting on a Rotating Body | Angular Momentum and Its Conservation | Rolling Motion
Rotational Motion :
When an object of finite size namely as extended bodies such as wheel rotates about its axis, then its motion cannot be analysed by considering it as a particle. This is due to the fact that at any given time, different parts of the object have different linear velocities and linear accelerations.
So, to further analysis on the object, it is considered as a system of particles. It must be noted that each particle has its own linear velocity and linear acceleration. In rotational motion, the motion of such system of particles will be discussed.
Fundamental Terms Used in Rotational Motion
Rigid Body : Ideally, a body is said to be a rigid body when it has a perfectly definite shape and size and the distances between particles of such a body do not change while applying an external force on it
e.g. A wheel can be considered as rigid body by ignoring change in its shape.
The rigid body may have two kinds of motion as follows:
- Pure Translational Motion :In pure translational motion, at any instant of time all particles of the body have the same velocity. e.g. A block of square shape moving on a plane surface.
- Pure Rotational Motion : In pure rotational motion, every particle of the rigid body moves in circles of different radii about a fixed line, which is known as axis of rotation. e.g. An oscillating fan.
Some rigid bodies may have a rolling motion, which is the combination of rotation and translation. e.g. A cylinder rolls down on inclined plane.
Centre of Mass : A point at which the entire mass of the body or system of bodies is supposed to be concentrated is known as the centre of mass.
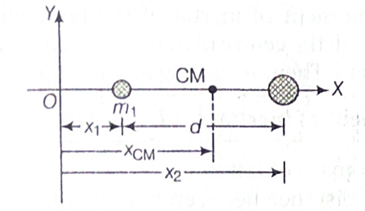
Let us consider the system of two particles of masses m1 and m2, their distance x1 and x2 respectively from origin O.
Then, the centre of mass of the system at a point, which is at distance of xCM, from O is given by
Center of Mass xCM= \frac{m_1x_1+m_2x_2}{m_1+m_2}
Where M=m1+m2 = Total mass of system
Moment of Inertia : The inability of a body to change its state of rest or of uniform linear motion by itself is known as inertia. Similarly, a body rotating about an axis is unable to produce a change in its rotational motion by itself. This inertness in this case is known as rotational inertia or moment of inertia.
The moment of inertia of a rigid body about any axis of rotation is the sum of the product of masses of the particles and the square of their respective distances from axis of rotation.
I= MR2 =m1r12 + m2r22 +... + mnrn2
Moment of Inertia I=\sum \limits_{i=1}^{n}m_1r_1^2
It is a scalar quantity. Its unit is kg-m2 and dimensions [ML2].
Moment of inertia of a body depends upon the following factors :
- Mass, shape and size of the body.
- Distribution of mass in the body about an axis of rotation.
- Position and orientation of the axis of rotation.
Moment of Inertia of large Rigid Body :
Let us consider a body of n particles of masses m1, m2,..., mn, with r1, r2,..., rn as their respective distances from axis of rotation as shown in figure.
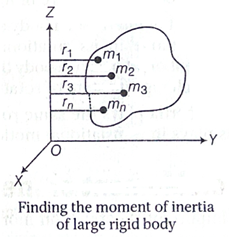
Then, moment of inertia of the body is given by
I= m1r12 + m2r22 +... + mnrn2
OR
I=\sum \limits_{i=1}^{n}m_ir_i^2
Physical Significance of Moment of Inertia
The unwillingness of a body to change its state of rest or of uniform motion along a straight line is called as Inertia.
The greater is the mass of a body, the greater is the force required to change its state of motion alongs a straight line.
Thus the mass of a body is a measure of its inertia.
Similarly, the moment of intertia of a body about an axis of rotation resists a change in its rotational motion. The greater of the moment of intertia of a body the greater is the torque required to change its state of rotation.
Thus, moment of inertia plays the same role in rotational motion as mass plays in translational motion,
Theorem on Moment of Inertia
There are two important theorems on moment of inertia, which, in some cases, enable the moment of inertia of a body to be determined about an axis, if its moment of inertia about some other axis is known. Let us now discuss both of them.
Theorem of Parallel Axes
It states that, “The moment of inertia of a body about an axis is equal to sum of moments of inertia of the body about a parallel axis passing through its centre of mass and the product of its mass and the square of distance between the two parallel axes”.
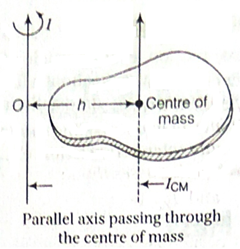
Let I be the moment of inertia of the body about an axis passing through point O. Take another parallel axis of rotation passing through the centre of mass of the body. Let ICM be the moment of inertia of the body about the axis passing through the centre of mass the distance between two parallel axis is h. Then, according to theorem of parallel axes
Moment of inertia, I = ICM + Mh2
where, M = mass of lamina
h = distance between two parallel axes.
Theorem of Perpendicular Axes :
It states that,
“The moment of inertia of a planar body (lamina) about an axis perpendicular to its plane is equal to the sum of its moments of inertia about two mutually perpendicular in its own pane and intersecting each at the point where the perpendicular axis passes through the body (lamina)”.
Let IXX, IYY and IZZ, be the moment of inertia of the lamina about OX,OY and OZ-axes respectively. Then, theorem of perpendicular axis gives
Moment of inertia IZZ = IXX + IYY
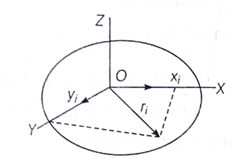
Perpendicular axes showing a planar body, where x and y are perpendicular axes and Z is perpendicular to the plane.
Radius of Gyration : Radius of gyration (K) of a body about an axis is the effective distance of a point from this axis, where the whole mass can be assumed to be concentrated, so that the moment of inertia remains the same.
Thus
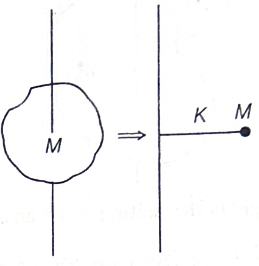
Finding the radius of gyration
I=MK2
Or Radius of gyration K = \sqrt{\frac{I}{m}}
e.g. Radius of gyration of a disc about an axis perpendicular to its plane and passing through its centre of mass is
K=\sqrt{\frac{\frac{1}{2}MR^2}{M}}=\frac{R}{\sqrt{2}}
Kinetic Energy of Rotating body : The kinetic energy of the rotating body is the energy which is possessed by the body by virtue of its rotational motion.
Sometimes it is called the rotational kinetic energy:
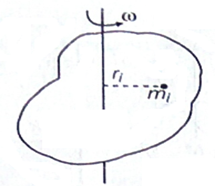
A rigid body rotating about an axis
Suppose a rigid body is rotating about a fixed axis with angular speed ω. Then, kinetic energy of the rigid body will be
K=\sum \limits_{i}\frac{1}{2}m_1v_1^2
= \sum \limits_{i}\frac{1}{2}m_1(ωr_i)^2
= \frac{1}{2}ω^2\sum \limits_{i}\frac{1}{2}m_1r_i^2
= \frac{1}{2}Iω^2 ........(given \(I=\sum\limits{m_1r_1^2}\\)
Thus Kinetic Energy KE = \frac{1}{2}Iω^2
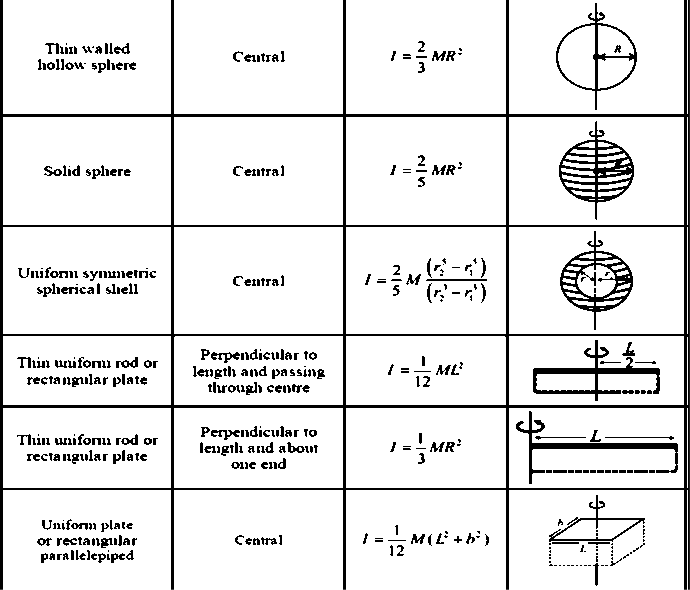
Moment of Inertia in Some Standard Cases:
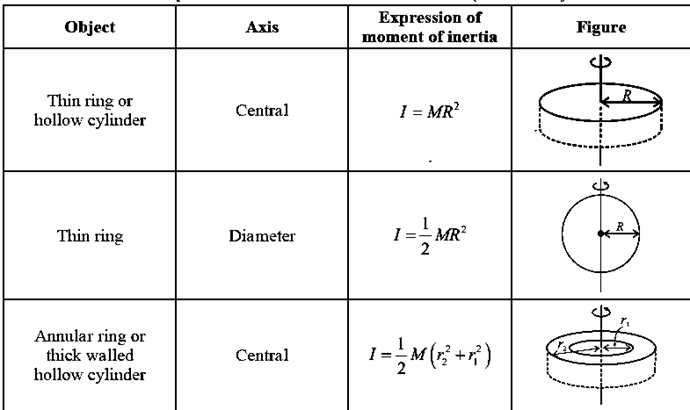
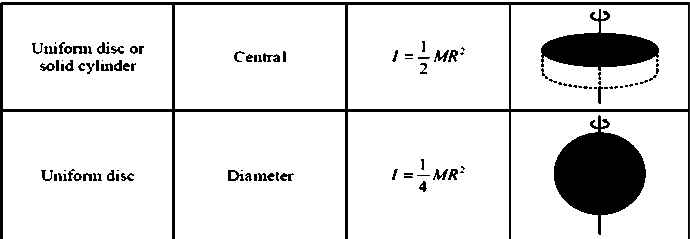

Torque Acting on a Rotating Body : The ability of force to produce rotational motion is called moment of force or torque. Suppose a force F is acting on a particle P and let r be the position vector of this particle about some reference point O. The torque of this force F, about O is defined as
Torque, τ = r x F |τ| = | r x F l = r F sinθ
[θ = angle between r and F]
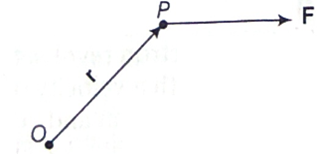
Finding the torque about a point
This is a vector quantity having its direction perpendicular to both r and F according to the rule of cross product. Its unit is N-m and dimensions [ML2T-2].
Torque of a Force about the Axis of Rotation
Consider a rigid body rotating about a fixed axis AB. Let F be a force acting on the body at point P. Take the origin O somewhere on the axis of rotation. The torque of F about O is defined as,
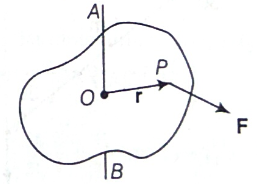
Force F acting at a point P on the rigid body
τ = r x F or τ = Iα
where
I = moment of inertia of the body about the axis of rotation
α = angular acceleration of the body
Torque produces only rotational motion of the body.
Work done by a torque τ in turning the body through a small angle dθ is dW = τdθ.
Or W = τθ.
Power of the torque, P = τ (dθ/dt) = τ.ω
Angular Momentum of a Particle : Angular momentum (L) can be defined as moment of line momentum about a point. The angular momentum of a particle of mass m moving with velocity v (having a linear momentum p = mv) about a point O is defined by the vector product of linear momentum and the position vector of that particle. Mathematically, it can be given as
L=r x p
or Angular momentum, L = m(r x v) [… p= mv]
where, L = angular momentum of particle about point O.
r = position vector of the particle about point O.
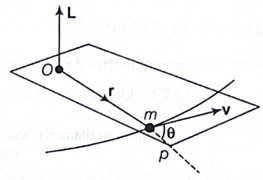
A particle moving about a point O
Some of the following observations are given:
1) Angular momentum is a vector quantity and its direction could be find out with the help of cross-product.
L=r.p=mvr […. p=mv|
= mr2ω […..v= rω]
= Iω […mr2 = I]
2) Magnitude of angular momentum depends on the position of point O and is given by
L = mvrsinθ
where, θ = angle between r and v.
3) L can be represented as L = r psinθ = r1p
where, r1 is the perpendicular distance of the linear momentum vector (p) from origin.
4) Angular momentum will be zero (L = O), if
P = 0 or r = 0 or θ = 0, 180°
Law of Conservation of Angular Momentum
We know that, τext = dL/dt
If τext =0, then dL/dt =0 or L must be a constant. Therefore, the law of conservation of angular momentum states that
“the angular momentum of a rotating body is conserved or remains constant, if the resultant external torque acting on the body is zero”.
As L = Iw the law of conservation of momentum leads us to the conclusion.
For an isolated system, Iw = constant
or I1w1 = I2w2
This principle is often made use by gymnast swimmers, Circus acrobats and ballet dancers, etc.
If external torque is acting on a body.
dL/dt = τext
τext dt = dL
Integrating this
J=L2-L1
Thus, the change in angular momentum is equal to the angular impulse of the torque.
Rolling Motion : Rolling motion can be considered as combination of translational motion of the centre of mass and rotational motion of the body about an axis passing through the centre of mass.
In this, axis of rotation is also in motion.
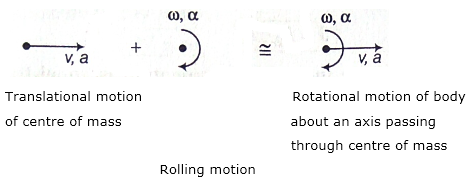
Hence in rolling motion, body possess both translational and rotational kinetic energy.
∴ Net kinetic energy = Translatory kinetic energy + Rotatory kinetic energy
KN =KT+KR= \frac{1}{2}mv^2 + \frac{1}{2}Iω^2
= \frac{1}{2}mv^2 + \frac{1}{2}mv^2\frac{k^2}{R^2} ..... [… I =mK2 and ω = v/R]
∴ Net kinetic energy, KN = \frac{1}{2}mv^2(1+\frac{k^2}{R^2})
Pure Rolling Motion : If the relative velocity of the point of contact (between body and platform) is zero, then the rolling motion is said to be pure rolling motion.
For pure rolling motion, vAB =0
i.e. (v-Rω)-v0 =0
v-Rω= v0
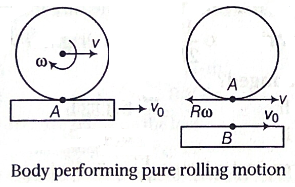
- If the platform is stationary, i.e. v0 = 0, then for pure rolling motion, v = Rw.
- In general, friction is responsible for pure rolling motion. In pure rolling motion, friction is static in nature.
- In pure rolling motion, friction is non-dissipative in nature, i.e. work done by frictional force is zero, this is because of the fact that point of contact is relatively at rest.
- In case of pure rolling motion, velocity of different particles of the body is as shown below.
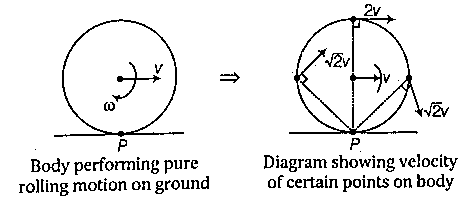
For above body, total kinetic energy is given by
K = KR + KT = \frac{Iω^2}{2} + \frac{mv^2}{2}
= \frac{Iω^2}{2} + \frac{m(Rω)^2}{2}
= \frac{(1+mR^2)ω^2}{2}
= \frac{I_Pω^2}{2}
Total kinetic energy, K = \frac{1}{2}I_Pω^2
where, IP =I+mR2 (the moment of inertia of a body passing through axis is at point of contact).
Rolling Motion on an Inclined Plane : We consider an inclined plane of q inclination on which a body performs pure rolling motion. At any instant t, the body is at a height h from the horizontal surface.
We suppose that body is released from height h,
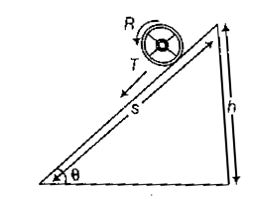
Rolling motion on an inclined plane
Comparison of Various Motions of a Body on an Inclined Plane :
1) Rolling Motion :
Velocity v_r = \sqrt{\frac{2gh}{β}} = \sqrt{\frac{2gh}{1+\frac{K^2}{R^2}}}
Acceleration a_r = \frac{gsinθ}{β} =\frac{gsinθ}{1+\frac{K^2}{R^2}}
Time of Descend T_r = \frac{1}{sinθ}\sqrt{\frac{2hβ}{g}}
2) Sliding Motion :
Velocity v_s = \sqrt{2gh}
Acceleration a_s = gsinθ
Time of Descend T_s = \frac{1}{sinθ}\sqrt{\frac{2h}{g}}
3) Falling Motion :
Velocity v_f = \sqrt{2gh}
Acceleration a_f = g
Time of Descend T_f = \sqrt{\frac{2h}{g}}
Impure rolling motion : In impure rolling motion, the point of contact of the body with the platform is not relatively at rest with respect to platform on which it is performing rolling motion, as a result sliding occurs at the point of contact, or impure rolling motion, VAB ≠ 0, i.e. v— Rω ≠ v0
If platform is stationary, i.e. v0 = o, then condition for pure rolling motion is v ≠ Rω.
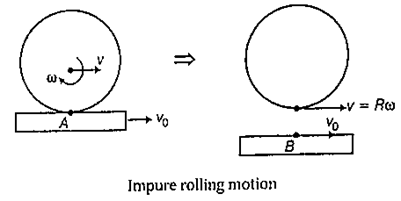
Here v ≠ Rω.. so a ≠ Rα
| Coming Soon........ online MCQ Test on this Topic and download solution with test result |