गुरुत्वाकर्षण
Based on Class 10 -विज्ञान आणि तंत्रज्ञान-भाग-१-पाठ-१- Maharashtra Board
Notes
|
अभ्यासघटक :
|
गुरुत्वाकर्षण :
एखाद्या वस्तुवर बल लावले असता, त्याचे वस्तूवर होणारे परिणाम :
- स्थिर वस्तू गतिमान होऊ शकते. उदाहरण : जमिनीवर स्थिर असलेल्या चेंडूला लाथ मारल्यास तो गतिमान होतो.
- गतिमान वस्तू स्थिर होऊ शकते. उदाहरण : ब्रेक वापरून सायकल थांबवता येते.
- वस्तूची चाल बदलू शकते. उदाहरण : गतिमान सायकलचे ब्रेक दाबले असता, सायकलची चाल कमी होते.
- वस्तूच्या गतीची दिशा बदलू शकते. उदाहरण : एकसमान चालीने वर्तुळाकार फिरणा-या वस्तूच्या गतीची दिशा प्रयुक्त बलामुळे सतत बदलत असते.
- वस्तूची चाल व वस्तूच्या गतीची दिशा, दोन्ही बदलू शकतात. उदाहरण : गोलंदाजाने टाकलेला चेंडू फलंदाजाने मारला असता, चेंड्ची चाल व चेंडूच्या गतीची दिशा दोन्ही बदलतात.
- वस्तूचा आकार तसेच वस्तूचे आकारमान यांत बदल होऊ शकतो. उदाहरण : रबरी चेंडू दाबला असता, तो गोलाकार न राहता त्याचा आकार बदलतो. तसेच त्याचे आकारमानही कमी होऊ शकते.
बलाचे प्रकार :
- गुरुत्वाकर्षण बल : गुरुत्वाकर्षण बल हे एक वैश्विक बल आहे. म्हणजेच बिश्वातील कोणत्याही दोन वस्तूमध्ये ते प्रयुक्त होते. उदाहरण : पृथ्वी व चंद्र यांमधील गुरुत्वीय बल,
- विद्युत चुंबकीय बल : दोन गतिमान विद्युत प्रभारांमधील बल.
- अणुकेंद्रकीय बल : अणुकेंद्रकातील प्रोटॉन्स व न्यूट्रॉन्स यांच्यामधील बल.
वर्तुळाकार गती (Circular motion) व अभिकेंद्री बल (Centripetal force) :
वर्तुळाकार कक्षेत फिरणाऱ्या कोणत्याही वस्तूवर वर्तुळाच्या केंद्राच्या दिशेने बल प्रयुक्त होत असते. या बलास अभिकेंद्री बल (Centripetal force) म्हणतात. म्हणजेच या बलामुळे वस्तू केंद्राकडे जाण्यास प्रवृत्त होते.
उदाहरण : पृथ्वीने चंद्रावर प्रयुक्त केलेल्या गुरुत्वीय बलामुळे चंद्र पृथ्वीभोवती फिरतो. हे बल पृथ्वीच्या केंद्राच्या दिशेने असते. त्याला अभिकेंद्री बल म्हणतात.
न्यूटनचे गतीविषयक असणारे तीन नियम :
- न्यूटनचा गतीविषयक पहिला नियम : जर एखादया वस्तृवर कोणतेही बाह्य असंतुलित बल कार्यरत नसेल, तर तिच्या विराम अवस्थेत किंवा सरळ रेषेतील एकसमान गतीमध्ये सातत्य राहते.
- न्यूटनचा गतीविषयक दुसरा नियम : संवेगपरिवर्तनाचा दर प्रयुक्त बलाशी समानुपाती असतो आणि संवेगाचे परिवर्तन बलाच्या दिशेने होते.
- न्यूटनचा गतीविषयक तिसरा नियम : प्रत्येक क्रिया बलास समान परिमाणाचे त्याच वेळी प्रयुक्त होणारे प्रतिक्रिया बल अस्तित्वात असते व त्यांच्या दिशा परस्परविरुद्ध असतात.
केप्लरचे नियम (Kepler’s Laws) :
केप्लरचा पहिला नियम : ग्रहाची कक्षा ही लंबवर्तुळाकार असून सूर्य त्या कक्षेच्या एका नाभीवर असतो.
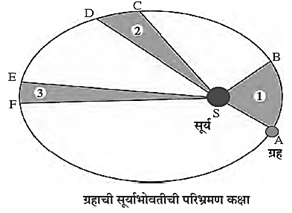
आकृती मध्ये ग्रहाची सूर्या भोवतीच्या परिभ्रमणाची लंबवर्तु ळाकार कक्षा दाखविली आहे. सूर्याची स्थिती S ने दर्शवली आहे.
केप्लरचा दुसरा नियम : ग्रहाला सूर्याशी जोडणारी सरळ रेषा, ही समान कालावधीत समान क्षेत्रफळ व्यापन करते.
- AB व CD ही ग्रहाने समान कालावधीत पार केलेली अंतरे आहेत म्हणजे समान कालावधी नंतर A व C पासून असलेले ग्रहाचे स्थान क्रमश: B व D ने दाखवले आहे.
- अकृतीमधील AS व CS या सरळ रेषा एका कालावधीत समान क्षेत्रफळ व्यापतात.
- समान कालावधीत ग्रहाचे विस्थापन A -> B, C -> D, E -> F असे होते.
- आकृतीमधील ASB, CSD व ESF ही क्षेत्रफले समान आहेत.
केप्लरचा तिसरा नियम : सूर्याची परिक्रमा करणाऱ्या ग्रहाच्या आवर्त कालाचा वर्ग हा ग्रहाच्या सूर्यापासूनच्या सरासरी अंतराच्या घनाला समानुपाती असतो. म्हणजे ग्रहाचा आवर्त काल हा T असेल व सूर्यापासून त्याचे सरासरी अंतर r असेल तर
T2 ∝ r3, म्हणजेच T2/ r3 = स्थिर = K ............. (1)
एकसमान वर्तु ळाकार गती / अभिकेंद्री बलाचे परिमाण (Uniform circular motion/Effect of centripetal force) :
गुरुत्वा कर्षणाचा नियम सांगताना न्यूटनने केप्लरच्या तिसऱ्या नियमाची मदत घेतली व बल हे अंतराच्या वर्गाच्या व्यस्त प्रमाणात असल्याचे (F ∝ 1/ r2 ) प्रतिपादन न्यूटनने केले.
प्रश्न- आकृतीसह सिद्ध करा गुरुत्वाकर्षणाचे बल, F ∝ 1/ r2.
सोयीसाठी आपण ग्रहाची कक्षा वर्तुळाकार घेऊ. येथे S (वर्तुळाचे केंद्र) हे सूर्याचे स्थान, P हे ठरावीक क्षणी ग्रहाचे स्थान व r म्हणजे वर्तुळाची त्रिज्या ( = सूर्य व ग्रह यांमधील , अंतर) होय. [आकृती ]
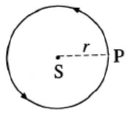
येथे ग्रहाची चाल एकसमान असून ती
![]() एवढी असते.
एवढी असते.
ग्रहाचे वस्तुमान m असल्यास ग्रहावर सूर्याने प्रयुक्त केलेले अभिकेंद्री बल (= गुरुत्वाकर्षणाचे बल),
F = mv2/r
F = \(\frac{m(2πr/T)^2}{r}=\frac{4π^2mr}{T^2}\)
आता केप्लरच्या तिसऱ्या नियमानुसार, T2 = Kr3
∴ F = \(\frac{4π^2mr}{Kr^3}=\frac{4π^2m}{K}(\frac{1}{r^2})\)
येथे, \(\frac{4π^2m}{K}\) = स्थिरांक.
∴ F ∝ 1/ r2
न्यूटनचा वैश्विक गुरुत्वाकर्षणाचा सिद्धांत (Newton’s universal law of gravitation) : विश्वातील प्रत्येक वस्तू इतर प्रत्येक वस्तूला ठराविक बलाने आकर्षित करत असते. हे बल एकमेकांना आकर्षित करणाऱ्या वस्तूच्या वस्तुमानांच्या गुणाकाराशी समानुपाती आणि त्यामधील अंतराच्या वर्गाशी व्यस्तानुपाती असते.
- न्यूटनचा गुरुत्वाकर्षणाचा सिद्धांत विश्वात सगळीकडे तसेच सगळ्या द्रव्यकणांना लागू होतो. म्हणून त्याला वैश्विक गुरुत्वाकर्षणाचा सिद्धांत म्हणतात
गुरुत्व बलाचे सूत्र : दोन वस्तूंची (अतिशय लहान व एकसमान घनता असलेल्या गोलांची) वस्तुमाने m1 व m2 असल्यास आणि त्या वस्तूंच्या केंद्रांमधील अंतर r असल्यास (r >>गोलांच्या त्रिज्या) (आकृती)

न्यूटनच्या गुरुत्वाकर्षणाच्या नियमानुसार यावस्तुंमधील गुरुत्वीय आकर्षण बलाचे परिमाण,
F ∝ m1m2 व F ∝ r2
∴ F ∝ \(\frac{m_1m_2}{r^2}\) ∴ F = G\((\frac{m_1m_2}{r^2})\)
येथे G हा स्थिरांक असून, त्यास वैश्विक गुरुत्वीय स्थिरांक म्हणतात.
- गुरुत्व स्थिरांकाचे मूल्य वस्तूचे (द्रव्यकणाचे) स्वरूप, वस्तुमान, आकारमान तसेच दोन वस्तूंमधील (द्रव्यकणांमधील) अंतर व माध्यम यांवर अवलंबून नसते. म्हणून त्याला वैश्विक गुरुत्वीय स्थिरांक म्हणतात.
- दोन द्रव्यकणांमधील गुरुत्वीय बल त्या कणांमधील माध्यमावर अवलंबून नसते.
| एखाद्या वस्तूचे वस्तुमानकेंद्र हे त्या वस्तूच्या आतील किंवा बाहेरील तो बिंदू असतो ज्यामध्ये वस्तूचे सर्व वस्तुमान केंद्रित असते असे मानू शकतो. एकसमान घनता असलेल्या गोलाकृती वस्तूचे वस्तुमानकेंद्र गोलाचे भूमितीय केंद्र असते. कोणत्याही समान घनता असलेल्या वस्तूचे वस्तुमानकेंद्र त्याच्या मध्यवर्ती बिंदूवर (Centroid)असते. |
न्यूटनच्या गुरुत्वाकर्षण सिद्धांताचे महत्त्व : या सिद्धांतामुळे पुढील गोष्टींचे स्पष्टीकरण मिळते :
- पृथ्वी आपल्यावर प्रयुक्त करीत असलेले गुरुत्वीय बल (चंद्र ब मानवनिर्मित उपग्रहांचे पृथ्वीभोवती फिरणे
- ग्रह, लघुग्रह, धूमकेतू इत्यादींचे सुर्यांभोवती फिरणे
- चंद्र ब सूर्य यांच्यामुळे समुद्रामध्ये येनारी भरती व ओहोटी.
वस्तूवरील पृथ्वीचे गुरुत्वीय बल : हे पृथ्वीच्या केंद्राच्या दिशेने असते. वस्तू पृथ्वीच्या पृष्ठभागावर असल्यास, ते बल F = G\((\frac{m_1m_2}{r^2})\) (चिन्हांचा अर्थ नेहमीप्रमाणे).
G चे मूल्य सर्वप्रथम हेन्री कॅवेण्डिश या शास्त्रज्ञाने प्रयोग करून मोजले. SI एकक प्रणालीत ते 6.673 x 10-11 Nm2/kg2 आहे.
- पृथ्वी सर्व वस्तूंना गुरुत्वीय बलाने आकर्षित करते. पृथ्वीचे वस्तुमानकेंद्र तिच्या केंद्रबिदूशी असल्याने ते गुरुत्व बल पृथ्वीच्या केंद्राच्या दिशेने असते.
- त्यामुळे आरंभी विराम अवस्थेत असलेली वस्तू क्षितिजलंब दिशेत सरळ खाली पडते.
- तसेच एखादी वस्तू क्षितिजलंब दिशेत सरळ वर फेकल्यास पृथ्वीच्या गुरुत्वीय बलामुळे तिचा वेग कमी होत जातो. काही वेळाने तो वेग शून्य होतो व त्यानंतर वस्तू सरळ खाली पडते.
पृथ्वीचे गुरुत्व त्वरण (Earth’s gravitational acceleration) : पृथ्वीच्या गुरुत्वीय बलामुळे वस्तूचे त्वरण होते. यास पृथ्वीचे गुरुत्व त्वरण म्हणतात. याची दिशा पृथ्वीच्या केंद्राकडे म्हणजे क्षितिजलंब दिशेत असते. याचे परिमाण g = \(\frac{Gm}{r^2}\) [r ≥ R (पृथ्वीची त्रिज्या) ] हे वस्तूच्या स्थानावर अवलंबून असते.
‘g’ च्या मूल्यात होणारे बदल
- पृथ्वीच्या पृष्ठभागावरील बदल : पृथ्वीच्या पृष्ठभागावरील सर्व ठिकाणी g चे मूल्य समान नसेल, याचे कारण असे की पृथ्वीचा आकार पूर्णपणे गोलाकार नाही. म्हणून तिच्या पृष्ठभागावरील वेगवेगळ्या बिंदूचे पृथ्वीच्या केंद्रापासूनचे अंतर त्या त्या बिंदूच्या स्थानानुसार बदलत असते. g चे मूल्य ध्रुवांवर सर्वात जास्त म्हणजे 9.832 m/s2 आहे व. विषुववृत्तावर g चे मूल्य सर्वात कमी म्हणजे 9.78 m/s2 आहे.
- g च्या मूल्यात उंचीनुसार होणारे बदल : पृथ्वीच्या पृष्ठभागाच्या वर जात असताना बिंदूचे केंद्रापासूनचे अंतर वाढत जाते व समीकरण प्रमाणे g चे मूल्य कमी होत जाते. पृथ्वीच्या पृष्ठभागापासून वस्तूची उंची पृथ्वीच्या त्रिज्येच्या तुलनेत खूप कमी असल्यास त्या उंचीमुळे g मध्ये होणारा बदल अल्प असतो.
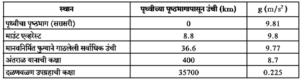
- खोलीनुसार बदल : पृथ्वीच्या आत जात असताना देखील g चे मूल्य बदलत राहते. समीकरण मधील r चे मूल्य कमी होत जाते व त्यानुसार g चे मूल्य अधिक व्हायला हवे. परंतु वस्तू पृथ्वीच्या केंद्राच्या जवळ गेल्यामुळे आता वस्तूवर गुरुत्वीय बल प्रयुक्त करणारा पृथ्वीचा भागही कमी होतो. म्हणजेच समीकरण मध्ये वापरले जाणारे M चे मूल्यही बदलते. याचा एकत्रित परिणाम म्हणून पृथ्वीच्या आत जात असताना खोलीनुसार g चे मूल्य कमी होत जाते.
न्यूटनच्या गुरुत्वाकर्षणाच्या सिदूधांतावरून गुरुत्वत्वरणाचे सूत्र :
समजा, m वस्तुमानाची एक वस्तू पृथ्वीच्या मध्यापासून (O) r अंतरावरून सोडली (आकृती ).
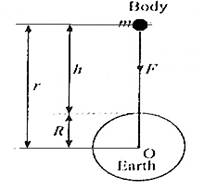
न्यूटनच्या गुरुत्वाकर्षणाच्या सिदुधांताप्रमाणे या वस्तूवरील पृथ्वीचे गुरुत्वीय बल F = \(\frac{GMm}{r^2}\)
येथे, M = पृथ्वीचे वस्तुमान व G = गुरुत्व स्थिरांक.
या बलामुळे वस्तूमध्ये निर्माण होणारे गुरुत्व त्वरण, g = बल/वस्तुमान = F/m ∴ g = \(\frac{GM}{r^2}\)
हे गुरुत्व त्वरणाचे सूत्र होय. हे त्वरण पृथ्वीच्या केंद्राच्या दिशेने असते.
पृथ्वीच्या पृष्ठभागापासून h एवढ्या उंचीवर, g = \(\frac{GM}{(R+h)^2}\) (…r = R + h) (येथे R = पृथ्वीची त्रिज्या)
पृथ्वीच्या पृष्ठभागावर h = 0 ∴ g = \(\frac{GM}{R^2}\)
पृथ्वीच्या पृष्ठभागावरील g चे मूल्य :
g चे SI एकक m/s2 आहे. पृथ्वीचे वस्तुमान 6 x 1024 kg व तिची त्रिज्या 6.4 x 106 m आहे. समीकरण g = \(\frac{GM}{R^2}\) प्रमाणे,
g = \(\frac{GM}{R^2}=\frac{(6.673×10^{-11})×(6×10^{24}}{(6.4×10^6)^2}\)= 9.77 m/s2 …..(G = 6.673 x 10-11 Nm2/kg2)
| पृथ्वी वरील एका स्थानावर g चे मूल्य सगळ्या वस्तूंसाठी एकसमान असते. म्हणून कुठल्याही दोन वस्तू, एकाच उंचीवरून सोडल्यास, एकाच वेळेस जमि नीवर पोहोचतात. त्यांचे वस्तुमान व इतर कुठल्याही गुणधर्मां चा या कालावधीवर परिणाम होत नाही. |
गुरुत्व स्थिरांक व गुरुत्व त्वरण,
| गुरुत्व स्थिरांक | गुरुत्व त्वरण |
| 1-एकक वस्तुमानाच्या दोन वस्तूंमधील अंतर एक एकक असल्यास त्यांच्यातील गुरुत्व बलाचे मूल्य गुरुत्व स्थिरांकाएवढे असते. | 1- पृथ्वीच्या गुरुत्व बलामुळे वस्तूचे त्वरण होते. या त्वरणाला गुरुत्व त्वरण म्हणतात. |
| 2-याचे मूल्य विश्वात सगळीकडे सारखे असते. | 2- याचे मूल्य स्थानानुसार बदलते. |
| 3- याला परिमाण असते, पण दिशा नसते. | 3- याला परिमाण व दिशा दोन्ही असतात. |
| 4-याचे SI एकक न्यूटन (N) आहे. | 4- याचे SI एकक m/s2 आहे. |
वस्तुमान व वजन :
| वस्तुमान | वजन |
| 1-कोणत्याही वस्तूचे वस्तुमान म्हणजे त्यामध्ये असलेल्या द्रव्यसंचयाचे मापन होय. | 1-एखाद्या वस्तूला पृथ्वी (अथवा इतर ग्रह/उपग्रह/तारा) ज्या गुरुत्वीय बलाने आकर्षित करते, त्या बलाला वस्तूचे वजन म्हणतात. |
| 2-वस्तूचे वस्तुमान विश्वात सगळीकडे सारखे असते व ते कधीही शून्य नसते. | 2-वस्तूचे वजन त्याच्या पृथ्वीसापेक्ष स्थानानुसार बदलते. पृथ्वीच्या केंद्राशी ते शून्य असते. |
| 3-वस्तुमान ही अदिश राशी असून तिचे SI एकक kg आहे. | 3-वजन ही सदिश राशी असून तिचे SI एकक न्यूटन (N) आहे. वजनाचे परिमाण = mg. |
m वस्तुमान असलेल्या वस्तूचे वजन, W = mg, येथे g म्हणजे गुरुत्व त्वरण होय. g चे मूल्य स्थानानुसार बदलते व ते ध्रुवांपेक्षा विषुववृत्तावर कमी असते.
मुक्त पतन (Free fall) :
एखादी वस्तू केवळ गुरुत्वीय बलाच्या प्रभावाने गतिमान असल्यास त्या गतीला मुक्त पतन म्हणतात.
एखादी वस्तू हवेत खाली पडत असताना तिच्यावर तीन बले कार्यरत असतात :
- अधोगामी दिशेने पृथ्वीचे गुरुत्व बल
- ऊर्ध्वगामी दिशेने हवेचे प्लावक बल
- वस्तूच्या वेगाच्या विरुद्ध दिशेने हवेचे घर्षण बल.
काही विशिष्ट परिस्थितीत प्लावक बल व घर्षण बल ही गुरुत्व बलाच्या तुलनेत नगण्य असतात. अशा वेळी (पृथ्वीच्या पृष्ठभागाजवळ) वस्तू जवळजवळ एकसमान त्वरणाने खाली पडते. एखादी वस्तू केवळ गुरुत्वीय बलाच्या प्रभावाने गतिमान असल्यास त्या गतीला मुक्त पतन म्हणतात. वास्तविक हे निर्वातातच शक्य असते. वस्तूच्या अशा खाली पडण्यास मुक्त पतन म्हणतात.
या बाबतीत गतिविषयक समीकरणे (चिन्हांचा अर्थ नेहमीप्रमाणे) :
v = u + gt, s = ut + \(\frac{1}{2}\)gt2 and v2 = u2 + 2gs
वस्तूचा आरंभ वेग शून्य असल्यास (u =0)
v = gt, s = \(\frac{1}{2}\)gt2 and v2 = 2gs
मुक्त पतनात जड व हलक्या या दोन्ही वस्तूंचे त्वरण समान असेल :
F = ma व F = \(\frac{GMm}{r^2}\) यावरून a = \(\frac{GM}{r^2}\) हे त्वरण वस्तूच्या वस्तुमानावर (m) अवलंबून नसते, हे स्पष्ट होते. त्यामुळे अधिक वस्तुमानाची वस्तू व कमी वस्तुमानाची वस्तू सारख्याच वेगाने खाली पडतात.
गुरुत्वीय स्थितिज ऊर्जा (Gravitational potential energy) :
वस्तू व पृथ्वी यांमधील गुरुत्वाकर्षणाच्या बलामुळे वस्तूत जी ऊर्जा सामावलेली असते, तिला गुरुत्वीय स्थितिज ऊर्जा म्हणतात.
वस्तूची गुरुत्वीय स्थितिज ऊर्जा = \(-\frac{GMm}{R+h}=-\frac{mgR^2}{R+h}\) …..(g = GM/R2, ∴ GM = gR2)
येथे, G = गुरुत्व स्थिरांक, M = पृथ्वीचे वस्तुमान, m = वस्तूचे वस्तुमान, R = पृथ्वीची त्रिज्या, h = वस्तूची पृथ्वीच्या पृष्ठभागापासूनची उंची.
मुक्तिवेग :
ज्या विशिष्ट आरंभ वेगामुळे पृथ्वीच्या (अथवा इतर ग्रहाच्या/उपग्रहाच्या/ताऱ्याच्या) पृष्ठभागापासून सरळ वर जाणारी वस्तू पृथ्वीच्या (अथवा त्या ग्रहाच्या/उपग्रहाच्या/ताऱ्याच्या ) गुरुत्वाकर्षणापासून मुक्त होते त्यास मुक्तिवेग म्हणतात. या वेळी वस्तू पृथ्वीपासून (अथवा त्या ग्रहापासून/उपग्रहापासून/ताऱ्यापासून ) अनंत अंतरावर जाऊन स्थिर होईल.
सामान्यत: वस्तू जमिनीवरून सरळ वर फेकल्यावर तिचा वेग कमी होत जाऊन कालांतराने ती पुन्हा जमिनीवर पडते. वस्तूचा आरंभ वेग वाढवल्यास ती जास्त उंच जाते व कालांतराने पुन्हा जमिनीवर पडते. आरंभ वेग संतत वाढवत गेल्यास एका विशिष्ट आरंभ वेगास वस्तू पृथ्वीच्या गुरुत्वाकर्षणापासून मुक्त होते. या वेगास मुक्तिवेग म्हणतात. या वेळी वस्तू पृथ्वीपासून अनंत अंतरावर जाऊन स्थिर होईल.
वस्तू पृथ्वीशी गुरुत्व बलामुळे बदध असल्याने तिची गुरुत्वीय स्थितिज ऊर्जा ऋण असते. वस्तूला \(+\frac{GMm}{R+h}-एवढी गतिज ऊर्जा दिल्यास वस्तूची एकूण ऊर्जा शून्य होऊन ती पृथ्वीपासून मुक्त होऊन पृथ्वीपासून अनंत अंतरावर जाऊन स्थिर होईल.
ऊर्जा अक्षय्यतेचा सिद्धांत वापरून मुक्तिवेगाचे सूत्र :
(येथे आपण हवेचे परिणाम विचारात घेणार नाही.)
समजा, m वस्तुमानाची वस्तू पृथ्वीच्या पृष्ठभागावरून सरळ वर मुक्ति-वेगाएवढ्या आरंभ वेगाने फेकली.
m = पृथ्वीचे वस्तुमान, R = पृथ्वीची त्रिज्या, G = गुरुत्व स्थिरांक व vesc = मुक्तिवेग,
वस्तू पृथ्वीच्या पृष्ठभागावर असताना तिची एकूण ऊर्जा,
E1 = गतिज ऊर्जा + स्थितिज ऊर्जा = \(\frac{1}{2}mv^2_{esc}+(-\frac{GMm}{R})\) = \(\frac{1}{2}mv^2_{esc}-\frac{GMm}{R}\)
फेकलेली वस्तू पृथ्वीपासून अनंत अंतरावर जाऊन स्थिर झाल्यावर तिची एकूण ऊर्जा,
E2 = गतिज ऊर्जा + स्थितिज ऊर्जा = \(\frac{1}{2}\)m(0)2 + \((-\frac{GMm}{∞})\) = 0 + 0 = 0
ऊर्जा अक्षय्यतेच्या सिद्धांतानुसार,
E1 = E2.
\(\frac{1}{2}mv^2_{esc}-\frac{GMm}{R}\)= 0
∴ \(\frac{1}{2}v^2_{esc}\) = \(\frac{GM}{R}\)
∴ \(v^2_{esc}\) = \(\frac{2GM}{R}\)
∴ vesc = \(\sqrt{\frac{2GM}{R}}\)
मुक्तिवेगाचे सूत्र g व R मध्ये :
मुक्तिवेग, vesc = \(\sqrt{\frac{2GM}{R}}\)
आता, g = GM/R2, ∴ GM = gR2
∴ vesc = \(\sqrt{\frac{2gR^2}{R}}=\sqrt{2gR}\)
मुक्तिवेगाचे सूत्र G, R व r (पृथ्वीची घनता) मध्ये
मुक्तिवेग, vesc = \(\sqrt{\frac{2GM}{R}}\)
पृथ्वीची घनता, ρ = वस्तुमान/आकारमान = \(\frac{M}{4/3πR^3}\)
∴ M = \(\frac{4}{3}\)πR3ρ
vesc = \(\sqrt{\frac{2G(4/3)πR^3ρ}{R}}\)
= \(\sqrt{2G(4/3)πR^2ρ}\)
= 2R\(\sqrt{\frac{2}{3}GπR^2ρ}\)
ग्रह सूर्याभोवती वर्तुळाकार कक्षेत फिरताना :
ग्रहावरील अभिकेंद्री बल = \(\frac{mv^2}{r}\) = ग्रहावरील सूर्याचे गुरुत्वीय बल = \(\frac{GMm}{r^2}\)
ग्रहाचे अभिकेंद्री त्वरण, a = \(\frac{v^2}{r}=\frac{(2πr/T)^2}{r}=\frac{4π^2r}{T^2}\)
ग्रहाचा आवर्तकाल T = \(\frac{2πr}{v}=\frac{2π}{\sqrt{GM}}r^{3/2}\) = \(\frac{2π}{\sqrt{gR^2}}r^{3/2}\)
|
महत्वाचे :
|
Useful links :
| Main Page : - Maharashtra Board Class 10-Marathi Medium - विज्ञान आणि तंत्रज्ञान-भाग-१ - All chapters notes, solutions, videos, test, pdf.
Next Chapter : विज्ञान आणि तंत्रज्ञान-भाग-१ -पाठ - 2- मूलद्रव्यां चे आवर्ती वर्गीकरण. - Online Notes |


I want your all Notes.This is my contact number- 7387575011
Click on “Buy” button to contact us on whatsapp