गुरुत्वाकर्षण
Based on Class 10 -विज्ञान आणि तंत्रज्ञान-भाग-१-पाठ-१- Maharashtra Board
Solutions
प्रश्न 1. खालील तक्त्यातील तीनही स्तंभातील नोंदी मधील संबंध लक्षात घेऊन त्याप्र माणे तक्ता परत लिहा.
| I | II | III |
| वस्तुमान | m/s2 | केंद्राजवळ शून्य |
| वजन | kg | जडत्वाचे माप |
| गुरुत्वत्वरण | N.m2/kg2 | संपूर्ण विश्वात सारखे |
| गुरुत्व स्थिरांक | N | उंचीवर अवलंबून आहे. |
| I | II | III |
| वस्तुमान | kg | जडत्वाचे माप |
| वजन | N | उंचीवर अवलंबून आहे. |
| गुरुत्वत्वरण | m/s2 | केंद्राजवळ शून्य |
| गुरुत्व स्थिरांक | N.m2/kg2 | संपूर्ण विश्वात सारखे |
प्रश्न 2. खालील प्रश्नां ची उत्तरे लिहा.
(अ) वजन व वस्तुमान यातील फरक काय आहे? एखाद्या वस्तूचे पृथ्वी वरील वस्तुमान व वजन मंगळावरही तेवढेच असतील का? का?
वस्तुमान व वजन :
| वस्तुमान | वजन |
| कोणत्याही वस्तूचे वस्तुमान म्हणजे त्यामध्ये असलेल्या द्रव्यसंचयाचे मापन होय. | एखाद्या वस्तूला पृथ्वी (अथवा इतर ग्रह / उपग्रह / तारा) ज्या गुरुत्वीय बलाने आकर्षित करते, त्या बलाला वस्तूचे वजन म्हणतात. |
| वस्तूचे वस्तुमान विश्वात सगळीकडे सारखे असते व ते कधीही शून्य नसते. | वस्तूचे वजन त्याच्या पृथ्वीसापेक्ष स्थानानुसार बदलते. पृथ्वीच्या केंद्राशी ते शून्य असते. |
| वस्तुमान ही अदिश राशी असून तिचे SI एकक kg आहे. | वजन ही सदिश राशी असून तिचे SI एकक न्यूटन (N) आहे. वजनाचे परिमाण = mg. |
- वस्तूचे वस्तुमान पृथ्वीवर व मंगळावर समान असेल, परंतु वजन मात्र समान नसेल, कारण g चे मंगळावरील मूल्य पृथ्वीवरील g च्या मूल्यापेक्षा वेगळे आहे.
(आ) मुक्त पतन, गुरुत्वत्वरण, मुक्तिवेग व अभिकेंद्री बल म्हणजे काय?
मुक्त पतन (Free fall) : एखादी वस्तू केवळ गुरुत्वीय बलाच्या प्रभावाने गतिमान असल्यास त्या गतीला मुक्त पतन म्हणतात.
गुरुत्वत्वरण : पृथ्वीच्या (अथवा इतर ग्रहाच्या / उपग्रहाच्या / ताऱ्याच्या) गुरुत्व बलामुळे वस्तूचे त्वरण होते. या त्वरणाला गुरुत्वत्वरण म्हणतात.
मुक्तिवेग : ज्या विशिष्ट आरंभ वेगामुळे पृथ्वीच्या (अथवा इतर ग्रहाच्या / उपग्रहाच्या / ताऱ्याच्या) पृष्ठभागापासून सरळ वर जाणारी वस्तू पृथ्वीच्या (अथवा त्या ग्रहाच्या/उपग्रहाच्या/ताऱ्याच्या ) गुरुत्वाकर्षणापासून मुक्त होते त्यास मुक्तिवेग म्हणतात.
अभिकेंद्री बल : वर्तुळाकार कक्षेत फिरणाऱ्या कोणत्याही वस्तूवर वर्तुळाच्या केंद्राच्या दिशेने बल प्रयुक्त होत असते. या बलास अभिकेंद्री बल म्हणतात.
(इ) केप्लरचे तीन नियम लिहा. त्यामुळे न्यूटनला आपला गुरुत्व सिद्धांत मांडण्यात कशी मदत झाली?
केप्लरचा पहिला नियम : ग्रहाची कक्षा ही लंबवर्तु ळाकार असून सूर्य त्या कक्षेच्या एका नाभीवर असतो.
आकृती मध्ये ग्रहाची सूर्या भोवतीच्या परिभ्रमणाची लंबवर्तु ळाकार कक्षा दाखविली आहे. सूर्याची स्थिती S ने दर्शवली आहे.
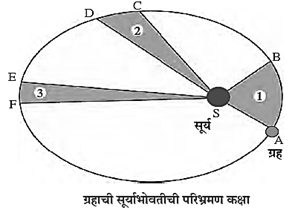
केप्लरचा दुसरा नियम : ग्रहाला सूर्याशी जोडणारी सरळ रेषा, ही समान कालावधीत समान क्षेत्रफळ व्यापन करते.
AB व CD ही ग्रहाने समान कालावधीत पार केलेली अंतरे आहेत म्हणजे समान कालावधी नंतर A व C पासून
असलेले ग्रहाचे स्थान क्रमश: B व D ने दाखवले आहे. आकृती मधील AS व CS या सरळ रेषा एका कालावधीत समान क्षेत्रफळ व्यापतात, समान कालावधीत ग्रहाचे विस्थापन A->B, C->D, E->F असे होते. आकृतीमधील ASB, CSD व ESFही क्षेत्रफले समान आहेत.
केप्लरचा तिसरा नियम : सूर्याची परिक्रमा करणाऱ्या ग्रहाच्या आवर्त कालाचा वर्ग हा ग्रहाच्या सूर्यापासूनच्या सरासरी अंतराच्या घनाला समानुपाती असतो. म्हणजे ग्रहाचा आवर्त काल हा T असेल व सूर्यापासून त्याचे सरासरी अंतर r असेल तर
T2 µ r3, म्हणजेच T2/ r3 = स्थिर = K ............. (1)
सोयीसाठी आपण ग्रहाची कक्षा वर्तुळाकार घेऊ. येथे S (वर्तुळाचे केंद्र) हे सूर्याचे स्थान, P हे ठरावीक क्षणी ग्रहाचे स्थान व r म्हणजे वर्तुळाची त्रिज्या ( = सूर्य व ग्रह यांमधील , अंतर) होय. [आकृती ]
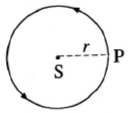
येथे ग्रहाची चाल एकसमान असून ती,
![]()
v = एवढी असते.
ग्रहाचे वस्तुमान m असल्यास ग्रहावर सूर्याने प्रयुक्त केलेले अभिकेंद्री बल (= गुरुत्वाकर्षणाचे बल),
F = mv2/r
F = \(\frac{m(2πr/T)^2}{r}=\frac{4π^2mr^2}{T^2r}=\frac{4π^2mr}{T^2}\)
आता केप्लरच्या तिसऱ्या नियमानुसार, T2 = Kr3
∴ F = \(\frac{4π^2mr}{Kr^3}=\frac{4π^2m}{K}(\frac{1}{r^3})\)
येथे, \(\frac{4π^2m}{K}\) = स्थिरांक.
∴ F ∝ 1/ r2
(ई) एक दगड u वेगाने वर फेकल्यावर h उंची पर्यंत पोचतो व नंतर खाली येतो. सिद्ध करा की त्याला वर जाण्यास जितका वेळ लागतो तितकाच वेळ खाली येण्यास लागतो.
गतीविषयक समीकरणे : v = u + at ……(1)
व s = ut + \(\frac 12\)at2 ….... (2)
समीकरण (1) व (2) वरून
s = (v − at)t + \(\frac 12\)at2 = vt − at2 + \(\frac 12\)at2
∴ s = vt − \(\frac 12\)at2 ... (3)
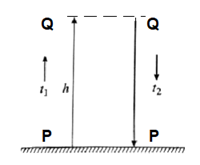
दगड वर जाताना (P→Q) [PQ = h] , s = h, t = t1 a = −g, u = u व v = 0
∴ समीकरण (3) वरून
h = 0 − \(\frac 12\)(−g)t12
∴ h = \(\frac 12\)gt12 ….... (4)
दगड खाली पडताना (Q → P)
t = t2, u = 0
∴ समीकरण (2) वरून h = \(\frac 12\)gt22 ….... (5)
समीकरणे (4) व (5) वरून, t12 = t22
∴ t1 = t2 ……(∵ t1 व t2 दोन्ही धन आहेत.)
(उ) समजा की g चे मूल्य अचानक दुप्पट झाले तर, एका जड वस्तूला जमिनीवरून ओढून नेणे दुपटीने अधिक कठीण होईल का? का?
होय. वस्तू जमिनीवरून ओढून नेताना वस्तू व जमिनीचा पृष्ठभाग यांमधील घर्षणबलाविरुद्ध कार्य करावे लागते. हे घर्षणबल वस्तूच्या वजनाशी समानुपाती असते. वस्तूचे वजन = mg.
g चे मूल्य अचानक दुप्पट झाले, तर वस्तूचे वजनही दुप्पट होईल. परिणामी वस्तू व जमिनीचा पृष्ठभाग यांमधील घर्षणबल पण दुप्पट होईल. त्यामुळे ती जड वस्तू जमिनीवरून ओढून नेणे दुपटीने अधिक कठीण होईल.
प्रश्न 3. पृथ्वी च्या केंद्रावर ‘g’ चे मूल्य शून्य असते याविषयी स्पष्टीकरण लिहा.
पृथ्वीच्या पृष्ठभागापासून केंद्राकडे जात असताना g चे मूल्य कमी होत जाते व पृथ्वीच्या केंद्राशी शून्य होते.
स्पष्टीकरण : पृथ्वी हा एकसमान घनतेचा व M वस्तुमान असलेला गोल आहे असे आपण मानू. खालील आकृती मध्ये दाखवल्याप्रमाणे पृथ्वीच्या पृष्ठभागाखाली d या खोलीवरील P हा बिंदू विचारात घ्या. या जागी m वस्तुमानाचा द्रव्यकण ठेवल्यास त्यावरील पृथ्वीचे गुरुत्वीय बल, F = \(\frac{GmM'}{(R-d)^2}\)
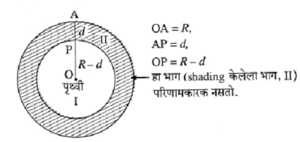
येथे R = पृथ्वीची त्रिज्या व M’ = (R – d) त्रिज्या असलेल्या गोलाचे वस्तुमान,
(R – d) = P चे पृथ्वीच्या केंद्रापासूनचे अंतर.
घनता = वस्तुमान / आकारमान
∴ वस्तुमान = आकारमान × घनता
∴ M’ = \(\frac 43\)π (R − d)3 × \(\frac{M}{\frac{4}{3}πR^3}\)
= \(\frac{M(R-d)^3}{R^3}\) येथे P च्या बाहेरील भाग (आकृती मधील भाग II) परिणामकारक नसतो.
P या स्थानी गुरुत्व त्वरण,
g = F/m = \(\frac{G}{(R-d)^2}×\frac{M(R-d)^3}{R^3}\)
= \(\frac{GM(R-d)}{R^3}\) याचे मूल्य पृथ्वीच्या पृष्ठभागावरील गुरुत्व त्वरणाच्या मूल्यापेक्षा \((\frac{GM}{R^2})\) कमी आहे. d वाढल्यास g चे मूल्य कमी होते व पृथ्वीच्या केंद्राशी g = 0 (‘.’ d = R)
प्रश्न 4. सिद्ध करा की, एका ताऱ्यापासून R अंतरावर असलेल्या ग्रहाचा परिभ्रमणकाल T आहे. जर तोच ग्रह 2R अंतरावर असल्यास त्याचा परिभ्रमणकाल T असेल.
T = \(\frac{2π}{\sqrt{GM}}R^{3/2}\), येथे,
T = ग्रहाचा ताऱ्याभोवतीच्या परिभ्रमणाचा आवर्तकाल, म्हणजेच परिभ्रमण काल,
M = ताऱ्याचे वस्तुमान,
G = गुरुत्व स्थिरांक
r = परिभ्रमण त्रिज्या, म्हणजेच ग्रहाचे ताऱ्यापासूनचे अंतर (ग्रहाची परिभ्रमण कक्षा वर्तुळाकार मानून).
आता, r = R असल्यास T = T1
∴ T1 = \(\frac{2π}{\sqrt{GM}}R^{3/2}\)
तसेच, r = 2R असल्यास T = T2
∴ T2 = \(\frac{2π}{\sqrt{GM}}(2R)^{3/2}\)
= \(\frac{2π}{\sqrt{GM}}R^{3/2}×2^{3/2}\) = T1 × 23/2
∴ T2 = \(\sqrt{8}\)T1 = \(\sqrt{8}\)T
प्रश्न 5. उदाहरणे सोडवा.
(अ) जर एका ग्रहावर एक वस्तू 5 m वरून खाली येण्यास 5 सेकंद घेत असेल तर त्या ग्रहावरील गुरुत्वत्वरण किती?
दिलेले : u = 0 m/s, s = 5 m, t = 5 s, g = ?
s = \(\frac 12\)gt2
∴ 5 = \(\frac 12\)g (5)2
∴ g =\(\frac 25\) m/s2 = 0.4 m/s2
त्या ग्रहावरील गुरुत्वत्वरण = 0.4 m/s2
(आ) ग्रह ‘क’ ची त्रिज्या ‘ख’ ग्रहाच्या त्रिज्येच्या अर्धी आहे. ‘क’ चे वस्तुमान MA आहे. जर ‘ख’ ग्रहावरील g चे मूल्य ‘क’ ग्रहावरील मूल्याच्या अर्धे असेल तर ‘ख’ ग्रहाचे वस्तुमान किती असेल?
दिलेले : ग्रह ‘क’ ची त्रिज्या RA = RB/2, ( …ग्रह ‘ख’ ची त्रिज्या = RB), ‘ख’ ग्रहावरील g चे मूल्य gB = gA/2
‘क’ चे वस्तुमान = MA ‘ख’ ग्रहाचे वस्तुमान MB = ?
g = \(\frac{GM}{R^2}\)
∴ gA = (\frac{GM_A}{R_A^2}\), gB = (\frac{GM_B}{R_B^2}\)
∴ gB /gA = \((\frac{R_A}{R_B})^2×\frac{M_B}{M_A}\)
∴ \(\frac 12\) = \((\frac 12)^2×\frac{M_B}{M_A}\)
∴ \(\frac{M_B}{M_A}\) = \(\frac 42\) = 2
∴ MB = 2 MA
∴ ख ग्रहाचे वस्तुमान = 2 MA
(इ) एका वस्तूचे वस्तुमान व पृथ्वी वरील वजन अनुक्रमे 5 kg व 49 N आहेत. जर चंद्रावर g चे मूल्य पृथ्वीच्या एक षष्ठांश असेल तर त्या वस्तू चे वस्तुमान व वजन चंद्रावर किती असेल?
दिलेले : m = 5 kg, WE = 49 N, gM (चंद्रावर) = gE (पृथ्वीवर)/6, mM (चंद्रावर) = ?, WM (चंद्रावर) = ?
(i) वस्तूचे चंद्रावर वस्तुमान = वस्तूचे पृथ्वीवर वस्तुमान = m
mM = mE = m = 5 kg. ….( ‘.’ वस्तूचे वस्तुमान विश्वात सगळीकडे सारखे असते )
(ii) W = mg
∴ \(\frac{W_M}{W_E}=\frac{mg_M}{mg_E}=\frac{g_M}{g_E}\)
∴ WM = WE × \(\frac{g_M}{g_E}\) = 49 × \(\frac 16\) = 8.167 N
(ई) एक वर फेकलेली वस्तू 500 मी उंचीपर्यंत जाते. तिचा आरंभीचा वेग किती असेल? त्या वस्तूस वर जाऊन परत खाली येण्यास किती वेळ लागेल? g = 10 m/s2
दिलेले : h = 500 m, g = 10 m/s2, v = 0 m/s, u = ?,
t (वस्तू वर जाण्यास) + t (वस्तू खाली येण्यास) = ?
वस्तू वर जाताना : v2 = u2 + 2as = u2 + 2(−g)h ….(‘.’ a = −g)
आता, v = 0 m/s, ∴ u2 = 2gh
∴ u2 = 2 x 10 x 500 = 10000 = (100 x 100) (m/s)2
∴ u = 100 m/s
वस्तूचा आरंभीचा वेग = 100 m/s
v = u + at = u – gt (‘.’ a = −g)
आता, v = 0 m/s, ∴ u = gt
∴ 100 = 10 x t
∴ वस्तू वर जाण्यास लागणारा वेळ, t = 10 s
आता, t (वस्तू खाली येण्यास) = t (वस्तू वर जाण्यास) t = 10 s …[ संदर्भासाठी वरील प्रश्न 2 (ई) पाहा.]
∴ t (वस्तू वर जाण्यास) + t (वस्तू खाली येण्यास) = 10 + 10 = 20 s
वस्तूस वर जाऊन परत खाली येण्यास 20 s लागतील.
(उ) एक चेंडू टेबलावरून खाली पडतो व 1 सेकंदात जमिनीवर पोचतो. g = 10 m/s2 असेल तर टेबलाची उंची व चेंडूचा जमिनीवर पोहोचतानाचा वेग किती असेल?
दिलेले : t = 1 s, g = 10 m/s2, u = 0 m/s, s = ?, v = ?
(i) s = ut + \(\frac 12\)gt2
येथे, u = 0 m/s ∴ s = \(\frac 12\)gt2
∴ s = \(\frac 12\) × 10 × (1)2 = 5 m
∴ टेबलाची उंची = 5 m
(ii) u = v + at = v + gt
= 0 + 10 × 1
= 10 m/s
चेंडूचा जमिनीवर पोहोचतानाचा वेग = 10 m/s
(ऊ) पृथ्वी व चंद्र यांची वस्तुमाने अनुक्रमे 6 x 1024 kg व 7.4 x 1022 kg आहेत व त्या दोन्हीमधील अंतर 3.84 x 105 km आहे. त्या दोन्हीमधील गुरुत्वबल किती असेल?
(दिलेले G = 6.7 x 10-11 Nm2/kg2.)
दिलेले : Me = 6 x 1024 kg, Mm = 7.4 x 1022 kg, r = 3.84 x 105 km = 3.84 x 108 m, G = 6.7 x 10-11 Nm2/kg2 , F = ?
F = \(\frac{Gm_Em_M}{r^2}\) = \(\frac{6.7×10^{-11}×6×10^{24}×7.4×10^{22}}{(3.84×10^8)^2}\)
= \(\frac{6.7×6×7.4×10^{35}}{3.84×3.84×10^{16}}\)
= 2.017 x 1020 N
हे पृथ्वी व चंद्र यांमधील गुरुत्व बल (परिमाण) होय.
(ए) पृथ्वीचे वस्तुमान 6 x 1024 kg आहे व तिचे सूर्या पासूनचे अंतर 1.5 x 1011 m आहे. जर त्या दोन्हीमधील गुरुत्व बल 3.5 x 1022 N असेल तर सूर्या चे वस्तुमान किती?
दिलेले : mE = = 6 x 1024 kg, r = 1.5 x 1011 m, F = 3.5 x 1022 N, G = 6.7 x 10-11 Nm2/kg2 , mS = ?
F = \(\frac{Gm_Em_S}{r^2}\)
∴ mS = \(\frac{Fr^2}{Gm_E}=\frac{3.5×10^{22}×(1.5×10^{11})^2}{6.67×10{-11}×6×10^{24}}\)
= 1.968 x 1030 kg
mS = 1.968 x 1030 kg (सूर्याचे वस्तुमान).
Useful links :
| Main Page : - Maharashtra Board Class 10-Marathi Medium - विज्ञान आणि तंत्रज्ञान-भाग-१ - All chapters notes, solutions, videos, test, pdf.
Next Chapter : विज्ञान आणि तंत्रज्ञान-भाग-१ -पाठ - 2- मूलद्रव्यां चे आवर्ती वर्गीकरण. - Online Solutions |
