Structure of Atoms
Based on NCERT Class 11th Chemistry Chapter 2
Exercise
Q 2.1: (i) Calculate the number of electrons which will together weigh one gram.
(ii) Calculate the mass and charge of one mole of electrons.
Answer: (i) Mass of one electron = 9.10939 × 10–31 kg = \(\frac{1}{9.10939 × 10^{-31}kg}\) × 1 × 10–3 kg = = 0.1098 × 10–3 + 31
Number of electrons that weigh 9.10939 × 10–31 kg = 1
Number of electrons that will weigh 1 g (1 × 10–3 kg)
= 0.1098 × 1028
= 1.098 × 1027
(ii) Mass of one electron = 9.10939 × 10–31 kg
Mass of one mole of electron = (6.022 × 1023) × (9.10939 ×10–31 kg)
= 5.48 × 10–7 kg
Charge on one electron = 1.6022 × 10–19 coulomb
Charge on one mole of electron = (1.6022 × 10–19 C) (6.022 × 1023)
= 9.65 × 104 C
Q2.2: (i) Calculate the total number of electrons present in one mole of methane.
(ii) Find (a) the total number and (b) the total mass of neutrons in 7 mg of 14C.
(Assume that mass of a neutron = 1.675 × 10–27 kg).
(iii) Find (a) the total number and (b) the total mass of protons in 34 mg of NH3 at STP. Will the answer change if the temperature and pressure are changed?
Answer: Answer 2.2: = 6.022 × 1023 × 10 = 6.022 × 1024 = \(\frac{6.022 × 10{23} × 8 × 7 mg }{14000 mg}\) = 2.4092 × 1021 (b) Mass of one neutron = 1.67493 × 10–27 kg (iii) (a) 1 mole of NH3 = 1 × (14) + 3 × (1)} g of NH3 Number of protons in 6.023 × 1023 molecules of NH3 = \(\frac{6.022 × 10{24} × 34 mg }{17000 mg}\) = 1.2046 × 1022 (b) Mass of one proton = 1.67493 × 10–27 kg The number of protons, electrons, and neutrons in an atom is independent of temperature and pressure conditions. Hence, the obtained values will remain unchanged if the temperature and pressure is changed.
(i) Number of electrons present in 1 molecule of methane (CH4) = 1 × (6) + 4 × (1) = 10
Number of electrons present in 1 mole i.e., 6.023 × 1023 molecules of methane.
(ii) (a) Number of atoms of 14C in 1 mole= 6.023 × 1023
Since 1 atom of 14C contains (14 – 6) i.e., 8 neutrons, the number of neutrons in 14 g of 14C is (6.023 × 1023) ×8. Or, 14 g of 14C contains (6.022 × 1023 × 8) neutrons.
Number of neutrons in 7 mg
Mass of total neutrons in 7 g of 14C
= (2.4092 × 1021) (1.67493 × 10–27 kg)
= 4.0352 × 10–6 kg
= 17 g of NH3
= 6.022 × 1023 molecules of NH3
Total number of protons present in 1 molecule of NH3
= 1×(7) + 3×(1)
= 10
= (6.023 × 1023) × (10)
= 6.023 × 1024
⇒ 17 g of NH3 contains (6.023 × 1024) protons. Number of protons in 34 mg of NH3
Total mass of protons in 34 mg of NH3
= (1.67493 × 10–27 kg) (1.2046 × 1022)
= 2.0176 × 10–5 kg
Q2.3: How many neutrons and protons are there in the following nuclei?
\(_{6}^{13}C,\, _{8}^{16}O,\, _{12}^{24}Mg,\, _{56}^{26}Fe,\, _{88}^{38}Sr \)
Answer: \(_{6}^{13}C\) Atomic mass = 13 \(_{8}^{16}O\) Atomic mass = 16 \(_{12}^{24}Mg\) Atomic mass = 24 \(_{56}^{26}Fe\) Atomic mass = 56 \(_{88}^{38}Sr\) Atomic mass = 88
Atomic number = Number of protons = 6
Number of neutrons = (Atomic mass) – (Atomic number)
= 13 – 6 = 7
Atomic number = 8
Number of protons = 8
Number of neutrons = (Atomic mass) – (Atomic number)
= 16 – 8 = 8
Atomic number = Number of protons = 12
Number of neutrons = (Atomic mass) – (Atomic number)
= 24 – 12 = 12
Atomic number = Number of protons = 26
Number of neutrons = (Atomic mass) – (Atomic number)
= 56 – 26 = 30
Atomic number = Number of protons = 38
Number of neutrons = (Atomic mass) – (Atomic number)
= 88 – 38 = 50
Q2.4: Write the complete symbol for the atom with the given atomic number (Z) and Atomic mass (A)
(i) Z = 17, A = 35
(ii) Z = 92, A = 233
(iii) Z = 4, A = 9
Answer: (i) \(_{17}^{35}Cl\) (ii) \(_{92}^{233}U\) (iii) \(_{4}^{9}Be\)
Q2.5: Yellow light emitted from a sodium lamp has a wavelength (λ) of 580 nm. Calculate the frequency (ν) and wave number (\(\bar v\)) of the yellow light.
Answer: From the expression λ = c/v We get, v = c/ λ ……….. (i) Where, ν = frequency of yellow light velocity of light in vacuum = 3 × 108 m/s Substituting the values in expression (i): v = ( 3 × 108 m/s) / (580 × 10–9 m) = 5.17 × 1014 s -1 Thus, frequency of yellow light emitted from the sodium lamp = 5.17 × 1014 s -1 \(\bar v\) = 1 / λ = 1 / (580 × 10–9 m) = 1.72 × 106 m-1
λ = wavelength of yellow light = 580 nm = 580 × 10–9 m
Wave number of yellow light
Q2.6: Find energy of each of the photons which
(i) correspond to light of frequency 3× 1015 Hz.
(ii) have wavelength of 0.50 Å.
Answer: Answer 2.6: Where, h = Planck’s constant = 6.626 × 10–34 Js (ii) Energy (E) of a photon having wavelength (λ) is given by the expression E= hc/ λ h = Planck’s constant = 6.626 × 10–34 Js c = velocity of light in vacuum = 3 × 108 m/s E = (6.626 × 10–34 Js) (3 × 108 m/s)/(0.50 × 10–15) = 3.976 × 10–15 J ∴ E = 3.98 × 10–15 J
(i) Energy (E) of a photon is given by the expression, E = hv
ν = frequency of light = 3 × 1015 Hz
Substituting the values in the given expression of E:
E = (6.626 × 10–34) (3 × 1015)
E = 1.988 × 10–18 J
Substituting the values in the given expression of E:
Q2.7: Calculate the wavelength, frequency and wave number of a light wave whose period is 2.0 × 10–10 s.
Answer: Frequency (ν) of light = \(\frac{1}{period}\) = \(\frac{1}{2.0 × 10^{-10}s}\) = 5 × 109 s-1 Wavelength (λ ) of light = \(\frac{c}{v}\) Where, λ = \(\frac{3 × 10^8}{5.0 × 10^{9}s}\) = 6×10-2 m Wave number \(\bar v\) of light = 1/ λ = 1/ 6×10-2 m = 1.66×101 m-1 = 16.66 m-1
c = velocity of light in vacuum = 3×108 m/s
Substituting the value in the given expression of λ:
Q2.8: What is the number of photons of light with a wavelength of 4000 pm that provide 1 J of energy?
Answer: Energy (E) of a photon = hν n= \(\frac{E_nλ}{hc}\) Where, λ = wavelength of light = 4000 pm = 4000 ×10–12 m c = velocity of light in vacuum = 3 × 108 m/s h = Planck’s constant = 6.626 × 10–34 Js Substituting the values in the given expression of n: n= \(\frac{1 × 4000 × 10^{-12} }{6.626 × 10^{-34} × 3 × 10^8 }\) = 2.012 × 1016 Hence, the number of photons with a wavelength of 4000 pm and energy of 1 J are
Energy (En) of ‘n’ photons = nhν
2.012 × 1016
Q2.9: A photon of wavelength 4 × 10–7 m strikes on metal surface, the work function of the metal being 2.13 eV. Calculate
(i) the energy of the photon (eV),
(ii) the kinetic energy of the emission, and
(iii) the velocity of the photoelectron (1 eV= 1.6020 × 10–19 J).
Answer: (i) Energy (E) of a photon = hν = hc/ λ Where, h = Planck’s constant = 6.626 × 10–34 Js λ = wavelength of photon = 4 × 10–7 m E = \(\frac{6.626 × 10^{-34} × 3 × 10^8 }{4 × 10^{-7} }\) = 4.9695 × 10-19 J Hence, the energy of the photon is 4.97 × 10–19 J. (ii) The kinetic energy of emission Ek is given by = hv -hv0 = (E-W)eV = ( \(\frac{4.6965 × 10^{-19} }{1.6020 × 10^{-19} }\) – 2.13 ) eV = (3.1020 – 2.13) eV Hence, the kinetic energy of emission is 0.97 eV. (iii) The velocity of a photoelectron (ν) can be calculated by the expression. \(\frac{1}{2} mv^2\) = hv -hv0 v = \(\sqrt{\frac{2(hv-hv_0)}{m}}\) where ( hv-hv0 ) is the kinetic energy of emission in Joules and ‘m’ is the mass of the photoelectron (ref – DISCOVERY OF SUB-ATOMIC PARTICLES, ELECTRON, PROTONS AND NEUTRONS for mass of electron). Substituting the values in the given expression of v: v = \(\sqrt{\frac{0.9720 × 1.6020 × 10^{-19}J }{9.01939 × 10^{-31}kg}}\) v = \(\sqrt{0.3418 × 10^{12}m^2s^{-2}}\) v = 5.84 × 105 ms–1 Hence, the velocity of the photoelectron is 5.84 × 105 ms–1.
c = velocity of light in vacuum = 3 × 108 m/s
Substituting the values in the given expression of E:
= 0.9720 eV
Q2.10: Electromagnetic radiation of wavelength 242 nm is just sufficient to ionize the sodium atom. Calculate the ionisation energy of sodium in kJ mol–1.
Answer: Energy of sodium (E) = \(\frac{N_Ahc}{λ}\) = \(\frac{(6.023 × 10^{23}mol^{-1})(6.626 × 10^{-34}Js)(3 × 10^8ms^{-1}) }{242 × 10^{-9}m}\) = 4.947 × 105 J mol–1
= 494.7 × 103 J mol–1
= 494 kJ mol–1
Q2.11: A 25 watt bulb emits monochromatic yellow light of wavelength of 0.57μm. Calculate the rate of emission of quanta per second.
Answer: Power of bulb, P = 25 Watt = 25 Js–1 = Substituting the values in the given expression of E: = \(\frac{(6.626 × 10^{-34}Js)(3 × 10^8ms^{-1}) }{0.57 × 10^{-6}m}\) E = 34.87 × 10–20 J = P/E = \(\frac{25 }{34.87 × 10^{-20}}\) = 7.169 x 1019s-1
Energy of one photon, E = hν = \(\frac{hc}{λ}\)
Rate of emission of quanta per second
Q 2.12:Electrons are emitted with zero velocity from a metal surface when it is exposed to radiation of wavelength 6800 Å. Calculate threshold frequency ( ) and work function (W0) of the metal.
Answer: Threshold wavelength of radiation λ0 = 6800 Å = 6800 × 10–10 m Threshold frequency v0 of the metal = c /λ0 = \(\frac{3 × 10^8ms^{-1}}{6800 × 10^{-10}m}\) = 4.41 × 1014 s–1 Hence, work function (W0) of the metal = hν0
Thus, the threshold frequency v0 of the metal is 4.41 × 1014 s–1
= (6.626 × 10–34 Js) (4.41 × 1014 s–1)
= 2.922 × 10–19 J
Q 2.13: What is the wavelength of light emitted when the electron in a hydrogen atom undergoes transition from an energy level with n = 4 to an energy level with n = 2?
Answer: The ni = 4 to nf = 2 transition will give rise to a spectral line of the Balmer series. The energy involved in the transition is given by the relation, E = 2.18 × 10–18 ×[\(\frac{1}{n_i^2} – \frac{1}{n_f^2}\)] Substituting the values in the given expression of E: = 2.18 × 10–18 ×[\(\frac{1}{4^2} – \frac{1}{2^2}\)] = 2.18 × 10–18 ×[\(-\frac{3}{16}\)] E = – (4.0875 × 10–19 J) λ = \(\frac{hc}{E}\) …….( since E = hν = \(\frac{hc}{λ}\)) Substituting the values in the given expression of λ: = \(\frac{(6.626 × 10^{-34}Js)(3 × 10^8ms^{-1}) }{4.0875 × 10^{-19}J}\) = 4.8631 x 10 -7 m = 486.31 x 10 -9 m = 486 nm
The negative sign indicates the energy of emission.
Wavelength of light emitted
Q2.14: How much energy is required to ionise a H atom if the electron occupies n = 5 orbit? Compare your answer with the ionization enthalpy of H atom (energy required to remove the electron from n =1 orbit).
Answer: The expression of energy is given by, \(\frac{(-2.18 × 10^{-18}Z^2) }{n^2}\) Where, ΔE = E∞ -E5 = \(\frac{(-2.18 × 10^{-18}J )× (1^2) }{∞^2}\) – \(\frac{(-2.18 × 10^{-18}J )× (1^2) }{5^2}\) = \(\frac{(-2.18 × 10^{-18}J )× (1^2) }{5^2}\) ……… ( since 1/∞ = 0) = 0.0872 x 10 -18 J ΔE = 0.0872 x 10 -18 J Hence, the energy required for ionization from n = 5 to n = ∞ is 8.72 x 10 -20 J Energy required for n1 = 1 to n = ∞ ΔE = E∞ -E1 = \(\frac{(-2.18 × 10^{-18}J )× (1^2) }{∞^2}\) – \(\frac{(-2.18 × 10^{-18}J )× (1^2) }{1^2}\) = 2.18 x 10 -18 J Hence, less energy is required to ionize an electron in the 5th orbital of hydrogen atom as compared to that in the ground state.
Z = atomic number of the atom n = principal quantum number
For ionization from n1 = 5 to n2 = ∞
Q2.15: What is the maximum number of emission lines when the excited electron of an H atom in n = 6 drops to the ground state?
Answer: When the excited electron of an H atom in n = 6 drops to the ground state, the following transitions are possible: Hence, a total number of (5 + 4 + 3 + 2 + 1) 15 lines will be obtained in the emission spectrum. The number of spectral lines produced when an electron in the nth level drops down to the ground state is given by = n(n-1)/2 Given, n = 6 Number of spectral lines = 6(6-1)/2 = 15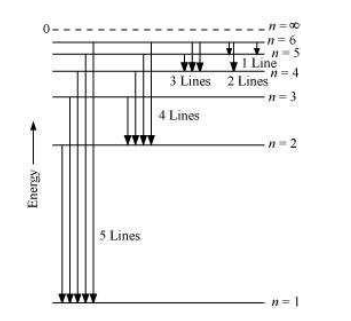
Q2.16: (i) The energy associated with the first orbit in the hydrogen atom is –2.18 × 10–18 J atom–1. What is the energy associated with the fifth orbit?
(ii) Calculate the radius of Bohr’s fifth orbit for hydrogen atom.
Answer: (i) Energy associated with the fifth orbit of hydrogen atom is calculated as: E5 = –2.18 × 10–18 J/(5)2 E5 = –8.72 × 10–20 J (ii) Radius of Bohr’s nth orbit for hydrogen atom is given by, rn = (0.0529 nm) n2
For, n = 5
r5 = (0.0529 nm) × (5)2
r5 = 1.3225 nm
Q2.17: Calculate the wave number for the longest wavelength transition in the Balmer series of atomic hydrogen.
Answer: For the Balmer series, ni = 2. Thus, the expression of wave number \(\bar v\) is given by, \(\bar v\) = \(\frac{1}{2^2} – \frac{1}{n_f^2}\) × 1.097 x 107 m-1 wave number \(\bar v\) is inversely proportional to wavelength of transition. Hence, for the longest wavelength transition \(\bar v\) has to be the smallest. For \(\bar v\) to be minimum, nf should be minimum. For the Balmer series, a transition from ni = 2 to nf = 3 is allowed. \(\bar v\) = \(\frac{1}{2^2} – \frac{1}{3^2}\) × 1.097 x 107 m-1 = \(\frac{9-4}{36} \) × 1.097 x 107 m-1 \(\bar v\) = 1.5236 ×106 m-1
Hence, taking nf = 3, we get:
Q2.18: What is the energy in joules, required to shift the electron of the hydrogen atom from the first Bohr orbit to the fifth Bohr orbit and what is the wavelength of the light emitted when the electron returns to the ground state?
The ground state electron energy is –2.18 × 10–11 ergs.
Answer: Energy (E) of the nth Bohr orbit of an atom is given by, En = \(\frac{(-2.18 × 10^{-18}Z^2) }{n^2}\) Where, ΔE = E5 – E1 = \(\frac{(-2.18 × 10^{-18} ×1^2) }{5^2}\) – (– 2.18 × 10–18) = ( 2.18 × 10–18) (\(\frac{(24 }{25}\)) = 2.0928 × 10–18 J wavelength of emitted light λ = \(\frac{hc}{E}\) = \(\frac{6.626 × 10^{-34} × 3 × 10^8 }{2.0928 × 10^{-18} }\) = 9.498 × 10–8 m
Z = atomic number of the atom
Ground state energy = – 2.18 × 10–11 ergs
= –2.18 × 10–11 × 10–7 J
= – 2.18 × 10–18 J
Energy required to shift the electron from n = 1 to n = 5 is given as:
Q2.19: The electron energy in hydrogen atom is given by En = (–2.18 × 10–18)/n2 J. Calculate the energy required to remove an electron completely from the n = 2 orbit. What is the longest wavelength of light in cm that can be used to cause this transition?
Answer: Given En = (–2.18 × 10–18)/n2 J Energy required for ionization from n = 2 is given by, ΔE = E∞ -E2 = \((\frac{-2.18 × 10^{-18}}{∞^2}) -(\frac{-2.18 × 10^{-18}}{2^2}) \)J ΔE = 5.45 × 10–19 J λ = hc/ΔE Here, λ is the longest wavelength causing the transition. =\( \frac{6.626 × 10^{-34} × 3 × 10^8 }{5.45 × 10^{-19} }\) = 3647 × 10–10 m
= 0.545 × 10–18 J
= 3647 Å
Q 2.20: Calculate the wavelength of an electron moving with a velocity of 2.05 × 107 ms–1.
Answer: According to de Broglie’s equation, λ = \(\frac{h}{mv}\) Where, λ = wavelength of moving particle m = mass of particle v = velocity of particle h = Planck’s constant λ = \(\frac{6.626 × 10^{-34}Js}{9.10939× 10^{-31}kg × 2.05 × 10^7ms^{-1}}\) λ = 3.548 × 10–11 m Hence, the wavelength of the electron moving with a velocity of 2.05 × 107 ms–1 is 3.548 × 10–11 m
Substituting the values in the expression of λ:
Q2.21: The mass of an electron is 9.1 × 10–31 kg. If its K.E. is 3.0 × 10–25 J, calculate its wavelength.
Answer: From de Broglie’s equation, λ = h/mv Given, Since K.E. = \(\frac{1}{2}mv^2\) ∴ Velocity v = \(\sqrt{2KE}{m}\) = \(\sqrt{\frac{2× (3.0 × 10^{-25}J)}{9.01939 × 10^{-31}kg}}\) = \(\sqrt{6.5866 × 10^4}\) v = 811.579 ms-1 Substituting the value in the expression of λ: = \(\frac{6.626 × 10^{-34} Js}{9.10939 × 10^{-31}kg × 811.579 ms^{-1} }\) λ = 8.9625 × 10–7 m Hence, the wavelength of the electron is 8.9625 × 10–7 m.
Kinetic energy (K.E) of the electron = 3.0 × 10–25 J
Q2.22 Which of the following are isoelectronic species i.e., those having the same number
of electrons?
Na+, K+, Mg2+, Ca2+, S2–, Ar.
Answer: Isoelectronic species have the same number of electrons.
Number of electrons in sodium (Na) = 11
Number of electrons in (Na+) = 10
A positive charge denotes the loss of an electron.
Similarly,
Number of electrons in K+ = 18
Number of electrons in Mg2+ = 10
Number of electrons in Ca2+ = 18
A negative charge denotes the gain of an electron by a species.
Number of electrons in sulphur (S) = 16
∴ Number of electrons in S2- = 18
Number of electrons in argon (Ar) = 18
Hence, the following are isoelectronic species:
(1) Na+ and Mg2+ (10 electrons each)
(2) K+, Ca2+, S2- and Ar (18 electrons each).
Q2.23: (i) Write the electronic configurations of the following ions:
(a) H– (b) Na+ (c) O2– (d) F–
(ii) What are the atomic numbers of elements whose outermost electrons are represented by (a) 3s1 (b) 2p3 and (c) 3p5?
(iii) Which atoms are indicated by the following configurations?
(a) [He] 2s1 (b) [Ne] 3s2 3p3 (c) [Ar] 4s2 3d1.
Answer: (i) (a) H– ion (b) Na+ ion (c) O2– ion (d) F– ion (ii) (a) 3s1 (c) 3p5 (iii) (a) [He] 2s1 Hence, the element with the electronic configuration [He] 2s1 is lithium (Li). (b) [Ne] 3s2 3p3 (c) [Ar] 4s2 3d1
The electronic configuration of H atom is 1s1.
A negative charge on the species indicates the gain of an electron by it.
Electronic configuration of H– = 1s2
The electronic configuration of Na atom is 1s2 2s2 2p6 3s1.
A positive charge on the species indicates the loss of an electron by it.
Electronic configuration of Na+ = 1s2 2s2 2p6 3s0 or 1s2 2s2 2p6
The electronic configuration of 0 atom is 1s2 2s2 2p4.
A dinegative charge on the species indicates that two electrons are gained by it.
Electronic configuration of O2– ion = 1s2 2s2 p6
The electronic configuration of F atom is 1s2 2s2 2p5.
A negative charge on the species indicates the gain of an electron by it.
Electron configuration of F– ion = 1s2 2s2 2p6
Completing the electron configuration of the element as
1s2 2s2 2p6 3s1.
∴ Number of electrons present in the atom of the element
= 2 + 2 + 6 + 1 = 11
∴ Atomic number of the element = 11
Completing the electron configuration of the element as
1s2 2s2 2p5.
∴ Number of electrons present in the atom of the element = 2 + 2 + 5 = 9
∴ Atomic number of the element = 9
The electronic configuration of the element is [He] 2s1 = 1s2 2s1.
∴ Atomic number of the element = 3
The electronic configuration of the element is [Ne] 3s2 3p3= 1s2 2s2 2p6 3s2 3p3.
∴ Atomic number of the element = 15
∴ Hence, the element with the electronic configuration [Ne] 3s2 3p3 is phosphorus (P).
The electronic configuration of the element is [Ar] 4s2 3d1= 1s2 2s2 2p6 3s2 3p6 4s2 3d1. Atomic number of the element = 21
∴ Hence, the element with the electronic configuration [Ar] 4s2 3d1 is scandium (Sc).
Q 2.24: What is the lowest value of n that allows g orbitals to exist?
Answer: For g-orbitals, l = 4.
As for any value ‘n’ of principal quantum number, the Azimuthal quantum number (l) can have a value from zero to (n – 1).
∴ For l = 4, minimum value of n = 5
Q2.25: An electron is in one of the 3d orbitals. Give the possible values of n, l and ml for this electron.
Answer: For the 3d orbital:
Principal quantum number (n) = 3
Azimuthal quantum number (l) = 2
Magnetic quantum number (ml) = – 2, – 1, 0, 1, 2
Q 2.26: An atom of an element contains 29 electrons and 35 neutrons. Deduce
(i) the number of protons and
(ii) the electronic configuration of the element.
Answer: (i) For an atom to be neutral, the number of protons is equal to the number of electrons. (ii) The electronic configuration of the atom is
∴ Number of protons in the atom of the given element = 29
1s2 2s2 2p6 3s2 3p6 4s2 3d10.
Q 2.27: Give the number of electrons in the species H2+ , H2, O2+
Answer: H2+ Number of electrons present in hydrogen molecule (H2) = 1 + 1 = 2 O2+ Number of electrons present in oxygen molecule (O2) = 8 + 8 = 16
∴ Number of electrons in H2+ = 2 – 1 = 1
H2:
Number of electrons in H2 = 1 + 1 = 2
∴ Number of electrons in O2+ = 16 – 1 = 15
Q2.28: (i) An atomic orbital has n = 3. What are the possible values of l and ml ?
(ii) List the quantum numbers (ml and l) of electrons for 3d orbital.
(iii) Which of the following orbitals are possible?
1p, 2s, 2p and 3f
Answer: (i) n = 3 (Given) (ii) For 3d orbital, l = 2. (iii) Among the given orbitals only 2s and 2p are possible. 1p and 3f cannot exist.
For a given value of n, l can have values from 0 to (n – 1).
∴ For n = 3
l = 0, 1, 2
For a given value of l, ml can have (2l + 1) values. For l = 0, m = 0 l = 1, m = – 1, 0, 1 l = 2, m = – 2, – 1, 0, 1, 2
For n = 3
l = 0, 1, 2 m0 = 0
m1 = – 1, 0, 1 m2 = – 2, – 1, 0, 1, 2
For a given value of l, ml can have (2l + 1) values i.e., 5 values.
∴ For l = 2 m2 = – 2, – 1, 0, 1, 2
For p-orbital, l = 1.
For a given value of n, l can have values from zero to (n – 1).
For l is equal to 1, the minimum value of n is 2.
Similarly,
∴ For f-orbital, l = 4.
For l = 4, the minimum value of n is 5.
Hence, 1p and 3f do not exist.
Q 2.29: Using s, p, d notations, describe the orbital with the following quantum numbers.
(a) n = 1, l = 0; (b) n = 3; l =1 (c) n = 4;l = 2; (d) n = 4; l =3.
Answer: (a) n = 1, l = 0 (Given) The orbital is 1s. (b) For n = 3 and l = 1 The orbital is 3p. (c) For n = 4 and l = 2 The orbital is 4d. (d) For n = 4 and l = 3 The orbital is 4f.
Q 2.30: Explain, giving reasons, which of the following sets of quantum numbers are not possible.
(a) n = 0, l = 0, ml = 0, ms = + ½
(b) n = 1, l = 0, ml = 0, ms = – ½
(c) n = 1, l = 1, ml = 0, ms = + ½
(d) n = 2, l = 1, ml = 0, ms = – ½
(e) n = 3, l = 3, ml = –3, ms = + ½
(f) n = 3, l = 1, ml = 0, ms = + ½
Answer: (a) The given set of quantum numbers is not possible because the value of the principal quantum number (n) cannot be zero. (b) The given set of quantum numbers is possible. (c) The given set of quantum numbers is not possible. (d) The given set of quantum numbers is possible. (e) The given set of quantum numbers is not possible. For n = 3, (f) The given set of quantum numbers is possible.
For a given value of n, ‘l ’ can have values from zero to (n – 1). For n = 1, l = 0 and not 1.
l = 0 to (3 – 1)
l = 0 to 2 i.e., 0, 1, 2
Q 2.31: How many electrons in an atom may have the following quantum numbers?
(a) n = 4, ms = – ½ (b) n = 3, l = 0
Answer: (a) Total number of electrons in an atom for a value of n = 2n2 (b) n = 3, l = 0 indicates that the electrons are present in the 3s orbital. Therefore, the number of electrons having n = 3 and l = 0 is 2.
For n = 4,
Total number of electrons = 2 (4)2 = 32
The given element has a fully filled orbital as
1s2 2s2 2p6 3s2 3p6 4s2 3d10.
Hence, all the electrons are paired.
∴ Number of electrons (having n = 4 and ms = – ½ ) = 16
Q2.32: Show that the circumference of the Bohr orbit for the hydrogen atom is an integral multiple of the de Broglie wavelength associated with the electron revolving around the orbit.
Answer: Since a hydrogen atom has only one electron, according to Bohr’s postulate, the angular momentum of that electron is given by: \(mvr\)=\(n\frac{h}{2π}\) ….. (1) Where, n = 1, 2, 3, … or mv = h/ λ …….. (2) Substituting the value of ‘mv’ from expression (2) in expression (1): hr/λ = \(n\frac{h}{2π}\) 2πr = nλ ……. (3) Since ‘2πr’ represents the circumference of the Bohr orbit (r), it is proved by equation (3) that the circumference of the Bohr orbit of the hydrogen atom is an integral multiple of de Broglie’s wavelength associated with the electron revolving around the orbit.
According to de Broglie’s equation: λ = h/mv
Q 2.33: What transition in the hydrogen spectrum would have the same wavelength as the Balmer transition n = 4 to n = 2 of He+ spectrum?
Answer: For He+ ion, the wave number \(\bar v\) associated with the Balmer transition, n = 4 to n \(\bar v\) = 1/λ =RZ2\((\frac{1}{n_1^2}-\frac{1}{n_2^2})\) Where, n1 = 2 n2 = 4 \(\bar v\) = 1/λ = R(2)2\((\frac{1}{2^2}-\frac{1}{4^2})\) = 4R(\(\frac{4-1}{16}\)) \(\bar v\) = 1/λ = \(\frac{3R}{4}\) λ = \(\frac{4}{3R}\) According to the question, the desired transition for hydrogen will have the same wavelength as that of He+. R(1)2 \((\frac{1}{n_1^2}-\frac{1}{n_2^2})\) = \(\frac{3R}{4}\) \((\frac{1}{n_1^2}-\frac{1}{n_2^2})\) = \(\frac{3}{4}\) ……. (1) By hit and trail method, the equality given by equation (1) is true only when
Z = atomic number of helium
n1 = 1 and n2 = 2.
The transition for n2 = 2 to n = 1 in hydrogen spectrum would have the same wavelength as Balmer transition n = 4 to n = 2 of He+ spectrum.
Q 2.34: Calculate the energy required for the process
He+(g) → He2+(g) + e–
The ionization energy for the H atom in the ground state is 2.18 × 10–18 J atom–1
Answer: Energy associated with hydrogen-like species is given by, En= – 2.18 × 10–18 \(\frac{Z^2}{n^2}\) J For ground state of hydrogen atom, ΔE = E∞ -E1 = 0 – (- 2.18 × 10–18 \(\frac{1^2}{1^2}\) J) ΔE = 2.18 × 10–18 J For the given process, He+(g) → He2+(g) + e– An electron is removed from n = 1 to n = ∞. ΔE = E∞ -E1 = 0 – (- 2.18 × 10–18 \(\frac{2^2}{1^2}\) J) = 8.72 × 10–18 J ∴ The energy required for the process = 8.72 × 10–18 J
Q 2.35: If the diameter of a carbon atom is 0.15 nm, calculate the number of carbon atoms which can be placed side by side in a straight line across length of scale of length 20 cm long.
Answer: 1 m = 100 cm = \(\frac{20 × 10^{-2}}{0.15 × 10^{-9}}\) = 133.33 × 107 = 1..33 × 109
1 cm = 10–2 m
Length of the scale = 20 cm
= 20 × 10–2 m
Diameter of a carbon atom = 0.15 nm
= 0.15 × 10–9 m
One carbon atom occupies 0.15 × 10–9 m.
∴ Number of carbon atoms that can be placed in a straight line
Q 2.36: 2× 108 atoms of carbon are arranged side by side. Calculate the radius of carbon atom if the length of this arrangement is 2.4 cm.
Answer: Length of the given arrangement = 2.4 cm = 1.2 × 10-10 m ∴ Radius of carbon atom = Diameter of carbon atom / 2 = 6.0 × 10-11 m
Number of carbon atoms present = 2 × 108
∴ Diameter of carbon atom = ( 2.4 × 10-2 m) / (2 × 108 )
Q 2.37: The diameter of zinc atom is 2.6Å .Calculate
(a) radius of zinc atom in pm and (b) number of atoms present in a length of 1.6 cm if the zinc atoms are arranged side by side lengthwise.
Answer: (a) = 2.6Å / 2 = 1.3 × 10-10 m = 130 × 10-12 m = 130 pm (b) Length of the arrangement = 1.6 cm = 6.153 × 107
Radius of zinc atom = Diameter / 2
= 1.6 × 10–2 m
Diameter of zinc atom = 2.6 × 10–10 m
∴ Number of zinc atoms present in the arrangement = (1.6 × 10–2 m) / ( 2.6 × 10–10 m)
Q2.38: A certain particle carries 2.5 × 10–16C of static electric charge. Calculate the number of electrons present in it.
Answer: Charge on one electron = 1.6022 × 10–19 C = (2.5 × 10–16 C )/ (1.6022 × 10–19 C) = 1560
⇒ 1.6022 × 10–19C charge is carried by 1 electron.
∴ Number of electrons carrying a charge of 2.5 × 10–16 C
Q 2.39: In Milikan’s experiment, static electric charge on the oil drops has been obtained by shining X-rays. If the static electric charge on the oil drop is –1.282 × 10–18C, calculate the number of electrons present on it.
Answer: Charge on the oil drop = 1.282 ×10–18C = 1.282 ×10–18C / 1.6022 × 10–19C = 8.0
Charge on one electron = 1.6022 × 10–19C
Number of electrons present on the oil drop
Q 2.40: In Rutherford’s experiment, generally the thin foil of heavy atoms, like gold, platinum etc. have been used to be bombarded by the α-particles. If the thin foil of light atoms like Aluminium etc. is used, what difference would be observed from the above results?
Answer: A thin foil of lighter atoms will not give the same results as given with the foil of heavier atoms.
Lighter atoms would be able to carry very little positive charge. Hence, they will not cause enough deflection of α-particles (positively charged).
Q 2.41: Symbols \(_{35}^{79}Br\) and \(^{79}Br\) can be written, whereas symbols \(_{79}^{35}Br\), and \(^{35}Br\), are not acceptable. Answer briefly.
Answer: The general convention of representing an element along with its atomic mass (A) and atomic number (Z) is \(_{Z}^{A}X\) Hence, \(_{35}^{79}Br\) is acceptable but \(_{79}^{35}Br\) is not acceptable. \(^{79}Br\) can be written but \(^{35}Br\) cannot be written because the atomic number of an element is constant, but the atomic mass of an element depends upon the relative abundance of its isotopes. Hence, it is necessary to mention the atomic mass of an element.
Q2.42: An element with mass number 81 contains 31.7% more neutrons as compared to protons. Assign the atomic symbol.
Answer: Let the number of protons in the element be x. x + 1.317 x = 81 x = 81 /2.317 x = 35 Hence, the number of protons in the element i.e., x is 35.
∴ Number of neutrons in the element
= x + 31.7% of x
= x + 0.317 x
= 1.317 x
According to the question,
Mass number of the element = 81
∴ (Number of protons + number of neutrons) = 81
Since the atomic number of an atom is defined as the number of protons present in its nucleus, the atomic number of the given element is 35.
∴ The atomic symbol of the element is \(_{35}^{81}Br\)
Q2.43: An ion with mass number 37 possesses one unit of negative charge. If the ion contains 11.1% more neutrons than the electrons, find the symbol of the ion.
Answer: Let the number of electrons in the ion carrying a negative charge be x. x = 18 Number of protons in the neutral atom = x – 1 = 17
Then,
Number of neutrons present
= x + 11.1% of x
= x + 0.111 x
= 1.111 x
Number of electrons in the neutral atom = (x – 1)
(When an ion carries a negative charge, it carries an extra electron)
∴ Number of protons in the neutral atom = x – 1
Given,
Mass number of the ion = 37
∴ (x – 1) + 1.111x = 37
2.111x = 38
∴ The symbol of the ion is \(_{17}^{37}Cr\)
Q2.44: An ion with mass number 56 contains 3 units of positive charge and 30.4% more neutrons than electrons. Assign the symbol to this ion.
Answer: Let the number of electrons present in ion A3+ be x. ∴ Number of neutrons in it = x + 30.4% of x = 1.304 x Given, Mass number of the ion = 56 ∴ (x + 3) + 1.304 x = 56 2.304 x = 53 ∴ x = 23 ∴ Number of protons = x + 3 = 23 + 3 = 26 ∴ The symbol of the ion \(_{26}^{56}Fe^{3+}\)
Since the ion is tri-positive,
⇒ Number of electrons in neutral atom = x + 3
∴ Number of protons in neutral atom = x + 3
Q 2.45: Arrange the following type of radiations in increasing order of frequency: (a) radiation from microwave oven (b) amber light from traffic signal (c) radiation from FM radio (d) cosmic rays from outer space and (e) X-rays.
Answer: The increasing order of frequency is as follows:
Radiation from FM radio < amber light < radiation from microwave oven < X- rays < cosmic rays
The increasing order of wavelength is as follows:
Cosmic rays < X-rays < radiation from microwave ovens < amber light < radiation of FM radio
Q2.46: Nitrogen laser produces a radiation at a wavelength of 337.1 nm. If the number of photons emitted is 5.6 × 1024, calculate the power of this laser.
Answer: Power of laser = Energy with which it emits photons Where, N = number of photons emitted = \((5.6 × 10^{24})(6.626 × 10^{-34} Js)(3 × 10^8 ms^{-1}) \over {(337.1 × 10^{-9}m)}\) = 0.3302 × 107 J
Power = E = \(Nhc \over λ\)
h = Planck’s constant
c = velocity of radiation
λ = wavelength of radiation
Substituting the values in the given expression of Energy (E):
= 3.33 × 106 J
Hence, the power of the laser is 3.33 × 106 J.
Q 2.47: Neon gas is generally used in the sign boards. If it emits strongly at 616 nm, calculate (a) the frequency of emission, (b) distance traveled by this radiation in 30 s (c) energy of quantum and (d) number of quanta present if it produces 2 J of energy.
Answer: Wavelength of radiation emitted = 616 nm = 616 × 10–9 m (Given) ν = \(c\over λ\) Where, c = velocity of radiation λ = wavelength of radiation ν = \(3.0 × 10^8 ms^{-1} \over {616 × 10^{-9} m}\) = 4.87 × 108 × 109 × 10–3 s–1 ν = 4.87 × 1014 s–1 Frequency of emission (ν) = 4.87 × 1014 s–1 (c) Energy of quantum (E) = hν (d) Energy of one photon (quantum) = 32.27 × 10–20 J = \( 2 J\over {32.27 × 10^{-20} J}\) = 6.19 ×1018
(a) Frequency of emission ν
Substituting the values in the given expression of ν
(b) Velocity of radiation, (c) = 3.0 × 108 ms–1
Distance travelled by this radiation in 30 s
= (3.0 × 108 ms–1) (30 s)
= 9.0 × 109 m
(6.626 × 10–34 Js) (4.87 × 1014 s–1)
Energy of quantum (E) = 32.27 × 10–20 J
Therefore, 32.27 × 10–20 J of energy is present in 1 quantum.
Number of quanta in 2 J of energy
= 6.2 ×1018
Q2.48: In astronomical observations, signals observed from the distant stars are generally weak. If the photon detector receives a total of 3.15 × 10–18 J from the radiations of 600 nm, calculate the number of photons received by the detector.
Answer: From the expression of energy of one photon (E), = \(hc\over λ\) Where, λ = wavelength of radiation h = Planck’s constant c = velocity of radiation Substituting the values in the given expression of E: E = \((6.626 × 10^{-34} Js)(3.0 × 10^8 ms^{-1}) \over {699 × 10^{-9} m}\) = 3.313 × 10–19 J Energy of one photon = 3.313 × 10–19 J = 3.15 × 10–18 J / 3.313 × 10–19 J = = 9.5
Number of photons received with 3.15 × 10–18 J energy
≈ 10
Q2.49: Lifetimes of the molecules in the excited states are often measured by using pulsed radiation source of duration nearly in the nano second range. If the radiation source has the duration of 2 ns and the number of photons emitted during the pulse source is 2.5 × 1015, calculate the energy of the source.
Answer: Frequency of radiation (ν), ν = \(1\over {2.0 × 10^{-9} s}\) ν = 5.0 × 108 s–1 E = (2.5 × 1015) (6.626 × 10–34 Js) (5.0 × 108 s–1) E = 8.282 × 10–10 J Hence, the energy of the source (E) is 8.282 × 10–10 J.
Energy (E) of source = Nhν
Where,
N = number of photons emitted, h = Planck’s constantm ν = frequency of radiation
Substituting the values in the given expression of (E):
Q2.50: The longest wavelength doublet absorption transition is observed at 589 and 589.6 nm. Calcualte the frequency of each transition and energy difference between two excited states.
Answer: (i) Given, \(c\over λ_1\) = \((3.0 × 10^8 ms^{-1}) \over {589 × 10^{-9} m}\) = 5.093 × 1014 s–1 And, frequency of second wavelength is v2 v2 =\(c\over λ_2\) = \((3.0 × 10^8 ms^{-1}) \over {589.6 × 10^{-9} m}\) = 5.088 × 1014s-1 (ii) Energy difference between two excited states is given as, = = 6.626 × 10-34 Js × 0.005 × 1014 s-1
Wavelength associated with first transition, λ1 =589 nm =589 × 10–9m
Wavelength associated with second transition, λ2 = 589.6 nm =589.6 × 10–9 m
Frequency of first wavelength is v1 =
ΔE = hv1 – hv2
Or, ΔE = h(v1 – v2)
= 6.626 × 10-34 Js × (5.093 × 1014 s-1 – 5.088 × 1014 s-1)
= 3.31 × 10-22 J
Q2.51: The work function for caesium atom is 1.9 eV. Calculate (a) the threshold wavelength and (b) the threshold frequency of the radiation. If the caesium element is irradiated with a wavelength 500 nm, calculate the kinetic energy and the velocity of the ejected photoelectron.
Answer: It is given that the work function (W0) for caesium atom is 1.9 eV. (a) From the W0 = \(hc \over λ_0\) λ0 = \(hc \over W_0\) Where, λ0 = threshold wavelength h = Planck’s constant c = velocity of radiation λ0 = \((6.626 × 10^{-34} Js)(3 × 10^8 ms^{-1}) \over {(1.9 × 1.602 × 10^{-19} J)}\) λ0 = 6.53 × 10–7 m Hence, the threshold wavelength λ0 is 653 nm. (b) From the expression, W0 = hν0, we get: ν0 = \(W_0 \over h\) Where, ν0 = threshold frequency h = Planck’s constant = \((1.9 × 1.602 × 10^{-19} J) \over {(6.626 × 10^{-34} Js)}\) …… (1 eV = 1.602 × 10–19 J) ν0 = 4.593 × 1014 s–1 (c) According to the question: = hc (\(\frac{1}{λ} – \frac{1}{λ_0}\) ) = 6.626 × 10-34 × 3 × 108 ( \(λ-λ_0 \over {λλ_0}\) ) = ( 6.626 × 10-34 )( 3 × 108) (\(((653-500)10^{-9}) \over {(653)(500)10^{-18}}\) ) = 9.3149 × 10–20 J Since K.E = \(\frac{1}{2}mv^2\) = 9.3149 × 10–20 J ν = \(\sqrt{2 × (9.3149 × 10^{-20} J) \over (9.10939 × 10^{-31}kg)}\) = \(\sqrt{2.0451 × 10^{11} m^2 s^{-2}} \) v = 4.52 × 105 ms–1
Substituting the values in the given expression of (λ0):
Substituting the values in the given expression of ν0:
Hence, the threshold frequency of radiation (ν0) is 4.593 × 1014 s–1
Wavelength used in irradiation (λ) = 500 nm
Kinetic energy = h (ν – ν0)
Kinetic energy of the ejected photoelectron = 9.3149 × 10–20 J
Hence, the velocity of the ejected photoelectron (v) is 4.52 × 105 ms–1.
Q2.52: Following results are observed when sodium metal is irradiated with different wavelengths. Calculate (a) threshold wavelength and, (b) Planck’s constant.
| λ (nm) | 500 | 450 | 400 |
| v × 10–5 (cm s–1) | 2.55 | 4.35 | 5.35 |
Answer: (a) Assuming the threshold wavelength to be λ0 (nm) = λ0 × 10-9 m the kinetic energy of the radiation is given as: h(v-v0) = \(\frac{1}{2}mv^2\) Three different equalities can be formed by the given value as: hc (\(\frac{1}{λ} – \frac{1}{λ_0}\) ) = \(\frac{1}{2}mv^2\) hc (\(\frac{1}{500 × 10^{-9}} – \frac{1}{λ_0 × 10^{-9}}\) ) = \(\frac{1}{2}m(2.55 × 10^5 × 10^{-2}) \) \(\frac{hc}{10^{-9}}\)(\(\frac{1}{500 } – \frac{1}{λ_0 }\) ) = \(\frac{1}{2}m(2.55 × 10^3)\) ….(1) Similarly, \(\frac{hc}{10^{-9}}\)(\(\frac{1}{450 } – \frac{1}{λ_0 }\) ) = \(\frac{1}{2}m(3.45 × 10^3)\) ….(2) \(\frac{hc}{10^{-9}}\)(\(\frac{1}{400 } – \frac{1}{λ_0 }\) ) = \(\frac{1}{2}m(5.35 × 10^3)\) ….(3) Dividing equation (3) by equation (1): So, threshold wavelength λ0 = 540 nm Note: part (b) of the question is not done due to the incorrect values of velocity given in the question.
Since K.E
Q2.53: The ejection of the photoelectron from the silver metal in the photoelectric effect experiment can be stopped by applying the voltage of 0.35 V when the radiation 256.7 nm is used. Calculate the work function for silver metal.
Answer: From the principle of conservation of energy, the energy of an incident photon (E) is equal to the sum of the work function (W0) of radiation and its kinetic energy (K.E) i.e., Where, c = velocity of radiation E = 4.83 eV The potential applied to silver metal changes to kinetic energy (K.E) of the photoelectron. Hence, K.E = 0.35 V K.E = 0.35 eV ∴ Work function, W0 = E – K.E = 4.83 eV – 0.35 eV
E = W0 + K.E
⇒ W0 = E – K.E
Energy of incident photon (E) = \(hc \over λ\)
h = Planck’s constant
λ = wavelength of radiation
Substituting the values in the given expression of E:
= 4.48 eV
Q2.54: If the photon of the wavelength 150 pm strikes an atom and one of its inner bound electrons is ejected out with a velocity of 1.5 × 107 ms–1, calculate the energy with which it is bound to the nucleus.
Answer: Energy of incident photon (E) is given by, E = \(hc\over λ\) Energy of the electron ejected (K.E) = 10.2480 × 10–17 J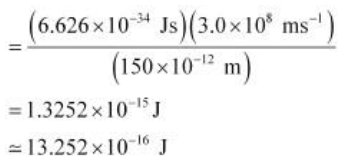
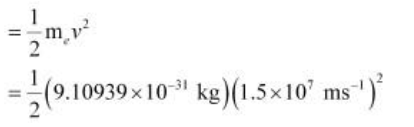
= 1.025 × 10–16 J
Hence, the energy with which the electron is bound to the nucleus can be obtained as:
= E – K.E
= 13.252 × 10–16 J – 1.025 × 10–16 J
= 12.227 × 10–16 J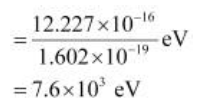
Q 2.55: Emission transitions in the Paschen series end at orbit n = 3 and start from orbit n and can be represented as v = 3.29 × 1015 (Hz) [1/32 – 1/n2]
Calculate the value of n if the transition is observed at 1285 nm. Find the region of the spectrum.
Answer: Wavelength of transition = 1285 nm Hence, for the transition to be observed at 1285 nm, n = 5.
= 1285 × 10–9 m (Given)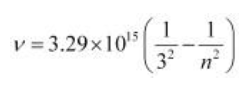

The spectrum lies in the infra-red region.
Q2.56: Calculate the wavelength for the emission transition if it starts from the orbit having radius 1.3225 nm and ends at 211.6 pm. Name the series to which this transition belongs and the region of the spectrum.
Answer: The radius of the nth orbit of hydrogen-like particles is given by, For radius (r1) = 1.3225 nm Similarly, ⇒ n1 = 5 and n2 = 2 = 1.097 × 107 (\(\frac {1}{2^2} -\frac{1}{5^2}\)) = 1.097 × 107 (\(\frac {21}{100}\) ) = 2.303 × 106 m–1 λ = \(\frac {1}{\bar v}\) = \(\frac {1}{2.303 × 10^6 m^{-1}}\) = 0.434 ×10–6 m λ = 434 nm
= 1.32225 × 10–9 m
= 1322.25 × 10–12 m
= 1322.25 pm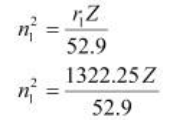
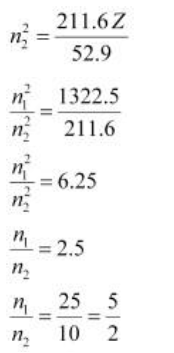
Thus, the transition is from the 5th orbit to the 2nd orbit. It belongs to the Balmer series.
wave number \(\bar v\) for the transition is given by,
Wavelength (λ) associated with the emission transition is given by,
Q 2.57: Dual behavior of matter proposed by de Broglie led to the discovery of electron microscope often used for the highly magnified images of biological molecules and other type of material. If the velocity of the electron in this microscope is 1.6 × 106 ms–1, calculate de Broglie wavelength associated with this electron.
Answer: From de Broglie’s equation, λ = \(\frac{h}{mv}\) = \(\frac{6.626 × 10^{-34}Js}{(9.10939 × 10^{-31}kg)(1.6 × 10^6 ms^{-1}}\) = 4.55 × 10–10 m λ = 455 pm de Broglie’s wavelength associated with the electron is 455 pm.
Q2.58: Similar to electron diffraction, neutron diffraction microscope is also used for the determination of the structure of molecules. If the wavelength used here is 800 pm, calculate the characteristic velocity associated with the neutron.
Answer: From de Broglie’s equation, λ = \(\frac{h}{mv}\) v = \(\frac{h}{mλ}\) Where, v = velocity of particle (neutron) h = Planck’s constant m = mass of particle (neutron) λ = wavelength Substituting the values in the expression of velocity (v), v = \(\frac{6.626 × 10^{-34}Js}{(1.67493 × 10^{-27}kg)(800 × 10^{-12} m}\) = 4.94 × 102 ms–1 v = 494 ms–1 ∴ Velocity associated with the neutron = 494 ms–1
Q 2.59: If the velocity of the electron in Bohr’s first orbit is 2.19 × 106 ms–1, calculate the de Broglie wavelength associated with it.
Answer: From de Broglie’s equation, λ = \(\frac{h}{mv}\) Where, v = velocity of particle h = Planck’s constant m = mass of particle (neutron) λ = wavelength Substituting the values in the expression of λ: λ = \(\frac{6.626 × 10^{-34}Js}{(9.10939 × 10^{-31}kg)(2.19 × 10^6 ms^{-1}}\) = 332 × 10-12 m = 332 pm ∴Wavelength associated with the electron = 332 pm
Q2.60: The velocity associated with a proton moving in a potential difference of 1000 V is 4.37 × 105 ms–1. If the hockey ball of mass 0.1 kg is moving with this velocity, calculate the wavelength associated with this velocity.
Answer: rom de Broglie’s equation, λ = \(\frac{h}{mv}\) Substituting the values in the expression, λ = \(\frac{6.626 × 10^{-34}Js}{0.1kg)(4.37 × 10^5 ms^{-1}}\) = 1.516 × 10-38 m
Q2.61: If the position of the electron is measured within an accuracy of + 0.002 nm, calculate the uncertainty in the momentum of the electron. Suppose the momentum of the electron is h/4πm × 0.05 nm, is there any problem in defining this value.
Answer: From Heisenberg’s uncertainty principle, Δx × Δp = \(\frac{h}{4π}\) ⇒ Δp = \(\frac{h}{(Δx)(4π)}\) Where, Δp = \(\frac{6.626 × 10^{-34}Js}{(0.002 nm)(4 × 3.14)}\) = \(\frac{6.626 × 10^{-34}Js}{(2 × 10{-12}m)(4 × 3.14)}\) = 2.637 × 10–23 Jsm–1 Uncertainty in the momentum of the electron = 2.637 × 10–23 kgms–1 Actual momentum = \(\frac{h}{(0.05nm)(4π_m)}\) = \(\frac{6.626 × 10^{-34}Js}{(5 × 10{-11}m)(4 × 3.14)}\) = 1.055 × 10–24 kgms–1 Since the magnitude of the actual momentum is smaller than the uncertainty, the value cannot be defined.
Δx = uncertainty in position of the electron
Δp = uncertainty in momentum of the electron
Substituting the values in the expression of Δp:
Δp = 2.637 × 10–23 kgms–1 (1 J = 1 kgms2s–1)
Q2.62: The quantum numbers of six electrons are given below. Arrange them in order of increasing energies. If any of these combination(s) has/have the same energy lists:
1. n = 4, l = 2, ml = –2 , ms = –1/2
2. n = 3, l = 2, ml= 1 , ms = +1/2
3. n = 4, l = 1, ml = 0 , ms = +1/2
4. n = 3, l = 2, ml = –2 , ms = –1/2
5. n = 3, l = 1, ml = –1 , ms= +1/2
6. n = 4, l = 1, ml = 0 , ms = +1/2
Answer: For n = 4 and l = 2, the orbital occupied is 4d. Hence, the six electrons i.e., 1, 2, 3, 4, 5, and 6 are present in the 4d, 3d, 4p, 3d, 3p, and 4p orbitals respectively.
For n = 3 and l = 2, the orbital occupied is 3d.
For n = 4 and l = 1, the orbital occupied is 4p.
Therefore, the increasing order of energies is 5(3p) < 2(3d) = 4(3d) < 3(4p) = 6(4p) < 1 (4d).
Q2.63: The bromine atom possesses 35 electrons. It contains 6 electrons in 2p orbital, 6 electrons in 3p orbital and 5 electrons in 4p orbital. Which of these electron experiences the lowest effective nuclear charge?
Answer: Nuclear charge experienced by an electron (present in a multi-electron atom) is dependent upon the distance between the nucleus and the orbital, in which the electron is present. As the distance increases, the effective nuclear charge also decreases. Among p-orbitals, 4p orbitals are farthest from the nucleus of bromine atom with (+35) charge. Hence, the electrons in the 4p orbital will experience the lowest effective nuclear charge. These electrons are shielded by electrons present in the 2p and 3p orbitals along with the s-orbitals. Therefore, they will experience the lowest nuclear charge.
Q2.64: Among the following pairs of orbitals which orbital will experience the larger effective nuclear charge? (i) 2s and 3s, (ii) 4d and 4f, (iii) 3d and 3p
Answer: Nuclear charge is defined as the net positive charge experienced by an electron in the orbital of a multi-electron atom. The closer the orbital, the greater is the nuclear charge experienced by the electron (s) in it. (i) The electron(s) present in the 2s orbital will experience greater nuclear charge (being closer to the nucleus) than the electron(s) in the 3s orbital. (ii) 4d will experience greater nuclear charge than 4f since 4d is closer to the nucleus. (iii) 3p will experience greater nuclear charge since it is closer to the nucleus than 3f.
Q2.65: The unpaired electrons in Al and Si are present in 3p orbital. Which electrons will experience more effective nuclear charge from the nucleus?
Answer: Nuclear charge is defined as the net positive charge experienced by an electron in a multi-electron atom.
The higher the atomic number, the higher is the nuclear charge. Silicon has 14 protons while aluminium has 13 protons. Hence, silicon has a larger nuclear charge of (+14) than aluminium, which has a nuclear charge of (+13). Thus, the electrons in the 3p orbital of silicon will experience a more effective nuclear charge than aluminium.
Q 2.66: Indicate the number of unpaired electrons in: (a) P, (b) Si, (c) Cr, (d) Fe and (e) Kr.
Answer: (a) Phosphorus (P): From the orbital picture, phosphorus has three unpaired electrons. (b) Silicon (Si): The electronic configuration of Si is: From the orbital picture, silicon has two unpaired electrons. From the orbital picture, chromium has six unpaired electrons. From the orbital picture, iron has four unpaired electrons. Since all orbitals are fully occupied, there are no unpaired electrons in krypton
Atomic number = 15
The electronic configuration of P is:
1s2 2s2 2p6 3s2 3p3
The orbital picture of P can be represented as: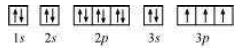
Atomic number = 14
1s2 2s2 2p6 3s2 3p2
The orbital picture of P can be represented as: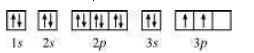
(c) Chromium (Cr):
Atomic number = 24
The electronic configuration of Cr is:
1s2 2s2 2p6 3s2 3p6 4s1 3d5
The orbital picture of chromium is:
(d) Iron (Fe):
Atomic number = 26
The electronic configuration is:
1s2 2s2 2p6 3s2 3p6 4s2 3d6
The orbital picture of chromium is:
(e) Krypton (Kr):
Atomic number = 36
The electronic configuration is:
1s2 2s2 2p6 3s2 3p6 4s2 3d10 4p6
The orbital picture of krypton is:
Q 2.67: (a) How many sub-shells are associated with n = 4?
(b) How many electrons will be present in the sub-shells having ms value of –1/2 for n = 4?
Answer: (a) n = 4 (Given) (b) Number of orbitals in the nth shell = n2 ∴Number of electrons with ms value of -1/2 = 16
For a given value of ‘n’, ‘l’ can have values from zero to (n – 1).
∴ l = 0, 1, 2, 3
Thus, four sub-shells are associated with n = 4, which are s, p, d and f.
For n = 4
Number of orbitals = 16
If each orbital is taken fully, then it will have 1 electron with ms value of -1/2