Rotational Dynamics
Class-12th-Physics-Chapter-1-Maharashtra Board
Notes-Part-1
|
Topics To Be Learn : Part-1 Characteristics of circular motion
|
Circular motion : The motion of a particle along a complete circle or a part of it is called circular motion.
Radius vector in circular motion: For a particle performing its position vector with respect to the centre of the circle is called the radius vector.
The radius vector has a constant magnitude equal to the radius of the circle. However, its direction changes as the position of the particle changes along the circumference.
Rotation : Circular motion of a body about an axis passing through the body is called rotation.
Revolution: Circular motion of a body around an axis outside the body is called revolution.
Characteristics of circular motion :
Angular displacement in circular motion : The change in the angular position of a particle performing circular motion with respect to a reference line in the plane of motion of the particle and passing through the centre of the circle is called the angular displacement.
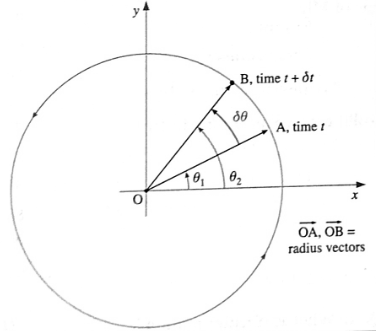
As the particle moves in its circular path, its angular position changes, say from θ1, at time t to θ2 at a short time δt later, see Fig. In the interval δt the position vector \(\vec{r}\) sweeps out an angle δθ = θ2 — θ1, δθ is the magnitude of the change in the angular position of the particle.
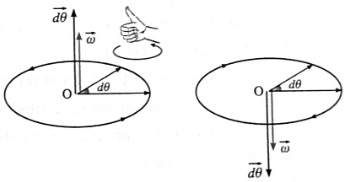
Infinitesimal angular displacement \(\vec{δθ}\). in an infinitesimal time interval δt → 0, is given a direction perpendicular to the plane of revolution by the right hand thumb rule.
Angular velocity : The time rate of angular displacement of a particle performing circular motion is called the angular velocity.
(i) If the particle has an angular displacement \(\vec{δθ}\) in a short time interval \(\vec{δt}\), its angular velocity
\(\vec{ω} = \lim\limits_{δt\to 0} \frac{\vec{δθ}}{δt} = \frac{\vec{δθ}}{δt}\)
(ii) \(\vec{ω}\) is a vector along the axis of rotation, in the direction of \(\vec{δθ}\) given by the right hand thumb rule.
[Angular speed, \(\vec{ω} = \frac{\vec{δθ}}{δt}\) is also called angular frequency]
Right hand thumb rule : If the fingers of the right hand are curled in the sense of revolution of the particle see Fig. then the outstretched thumb gives the direction of the angular displacement.
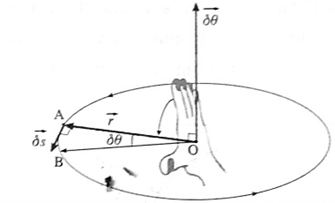
Linear velocity of a particle performing circular motion: OR Relation between the linear velocity and the angular velocity of a particle performing circular motion : Consider a particle performing circular motion in an anticlockwise sense, along a circle of radius r. In a very small time interval δt the particle moves from point A to point B through a distance δs and its angular position changes by δθ. δθ = \(\frac{arc\, AB}{radius} = \frac{δs}{r} \) As \(\vec{δt}\) → 0, B will be very dose to A and displacement \(\vec{AB}=\vec{δs}\) will be a straight Line perpendicular to radius vector \(\vec{OA}=\vec{r}\)By the right hand rule of cross product. \(\vec{δs}=\vec{δθ}×\vec{r}\) ∴ \(\lim\limits_{δt\to 0} \frac{\vec{δs}}{δt} = \lim\limits_{δt\to 0} \frac{\vec{δθ}}{δt}×\vec{r}\) ∴ \( \frac{\vec{δs}}{δt} = \frac{\vec{δθ}}{δt}×\vec{r}\) ............ (1) The linear velocity \(\vec{v}\) of the particle is the time rate of displacement and its angular velocity \(\vec{ω}\) is the time rate of angular displacement. \(∴ \vec{v}= \frac{\vec{δs}}{δt} and \, \vec{ω} = \frac{\vec{δθ}}{δt}\) Therefore, from Eq. (1), \(∴ \vec{v}=\vec{ω}×\vec{r}\) Since \(∴ \vec{ds}\) is tangential, the instantaneous linear velocity \(\vec{v}\) of a particle performing circular motion is along the tangent to the path, in the sense of motion of the particle. \(\vec{v}, \vec{ω} \,and\, \vec{r} \) are mutually perpendicular, so that in magnitude, v = ω r Relation between linear velocity and angular velocity of a particle in circular motion: Linear velocity \(\vec{v}=\vec{ω}×\vec{r}\) where \(\vec{ω}\) is the angular velocity and \(\vec{r}\)is the radius vector. At every instant, \(\vec{v}, \vec{ω} \,and\, \vec{r} \) are mutually perpendicular, so that in magnitude, v = ω r
Uniform circular motion (UCM): A particle is said to perform uniform circular motion if it moves in a circle or a circular arc at constant linear speed or constant angular velocity.
In a uniform motion, a particle covers equal distances in equal intervals of time. Any motion which repeats itself in equal intervals of time is called a periodic motion. In a uniform circular motion (UCM), the particle takes the same time to complete each revolution, a distance equal to the circumference of the circle. Therefore, it is a periodic motion.
Examples of UCM:
- Circular motion of every particle of the blades of a fan when rotating with a constant angular speed.
- Motion of the hands of a clock.
- Motion of an Earth-satellite in a circular orbit.
Period of revolution : The time taken by a particle performing uniform circular motion (UCM) to complete one revolution is called the period of revolution or the period (T) of UCM.
T = \(\frac{2πr}{v}= \frac{2πr}{ω}\)
where v and ω are the linear and angular speeds respectively.
SI unit : the second (s)
Dimensions : [M°L°T1 ].
Frequency of revolution :The number of revolutions per unit time made by a particle in UCM is called the frequency of revolution (f).
The particle completes 1 revolution in periodic time T. Therefore, it completes 1/ T revolutions per unit time.
Frequency f = \(\frac{1}{T} = \frac{v}{2πr} = \frac{ω}{2πr}\)
SI unit : the hertz (Hz), 1 Hz = 1 s-1
Dimensions : [M°L°T-1]
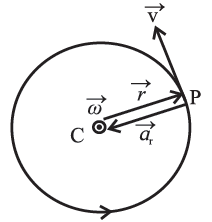
Acceleration of a particle in UCM: (Expression for the acceleration) A particle in uniform circular motion (UCM) moves in a circle or circular arc at constant linear speed v. The instantaneous linear velocity of the particle is along the tangent to the path in the sense of motion of the particle. Since \(\vec{v}\) changes in direction, without change in its magnitude, there must be an acceleration that must be (i) perpendicular to; (ii) constant in magnitude (iii) at every instant directed radially inward, i.e., towards the centre of the circular path. Such a radially inward acceleration is called a centripetal acceleration. \(\vec{a}=\frac{\vec{dv}}{dt}=\vec{a_r}\) If \(\vec{ω}\) is the constant angular velocity of the particle and r is the radius of the circle, \(\vec{a_r}=-ω^2\vec{r}\) where ω = |\(\vec{ω}\)| and the minus sign shows that the direction of \(\vec{a_r}\) is at every instant opposite to that of the radius vector \(\vec{r}\) In magnitude, \(\vec{a_r} = ω^2\vec{r} = \frac{v}{r} = ωv\) Diagram showing the linear velocity, angular velocity and radial acceleration of a particle performing circular motion with radius r.
Quantities that are uniform in UCM : Linear speed and angular speed. (Also, kinetic energy, angular speed and angular momentum.)
Quantities that are non-uniform in UCM : Velocity and acceleration, centripetal force are nonuniform in UCM.
Nonuniform Circular Motion: Consider a particle moving in a plane along a circular path of constant radius. If the particle is seeding up or slowing down, its angular speed w and linear speed v both change with time. Then the particle is said to be a nonuniform circular motion.
Angular acceleration : The time rate of change of angular velocity of a particle performing circular motion is called the angular acceleration.
(i) It \(\vec{dω}\) is the change in angular velocity in a short time interval δt, the angular acceleration
\(\vec{α} = \lim\limits_{δt\to 0} \frac{\vec{δω}}{δt} = \frac{\vec{dω}}{dt}\)
(i) The direction of \(\vec{α}\) is the same as that of \(\vec{dω}\) . We consider the case where a change in \(\vec{ω}\) arises due to a change in its magnitude only. If the particle is speeding up, i.e. ω is increasing with time, then \(\vec{α}\) is in the direction of \(\vec{dω}\) If the particle is slowing down, i.e. ω is decreasing with time, then \(\vec{α}\) is directed opposite to \(\vec{ω}\) .
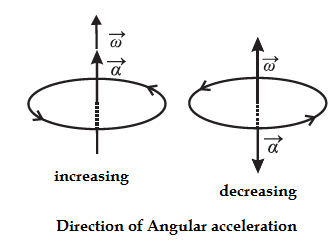
If the angular speed changes from ω1, to ω2 in time t, the magnitude (α) of the average angular acceleration is
α = \(\frac{ω_2-ω_1}{t}\)
Tangential acceleration of a particle in nonuniform circular motion :
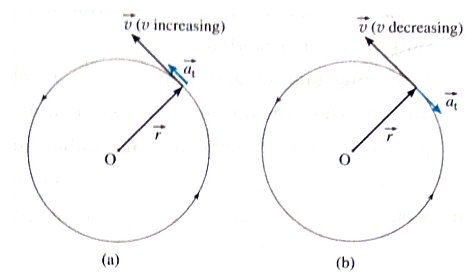
Tangential acceleration : For a particle performing circular motion, the linear acceleration tangential to the path that produces a change in the linear speed of the particle is called the tangential acceleration.
Explanation : If a particle performing circular motion is speeding up or slowing down, its angular speed w to and linear speed v both change with time. Tangential acceleration when linear speed is (a) increasing (b) decreasing The linear acceleration that produces a change only in the linear speed must be along \(\vec{v}\) . Hence, it is called the tangential acceleration \(\vec{a_t}\) . In magnitude, \(\vec{a_t}=\frac{dv}{dt}\) (ii) If the linear speed v of the particle is increasing, \(\vec{a_t}\) is in the direction of \(\vec{v}\). If v is decreasing \(\vec{a_t}\) directed opposite to \(\vec{v}\). see Fig.
Relation between the magnitudes of the linear (tangential) acceleration and angular acceleration in nonuniform circular motion & an expression for the resultant acceleration of a particle in terms of tangential and radial components. :
(i) Consider a particle moving along a circular path of constant radius w. If the particle is speeding up or slowing down, its motion is nonuniform, and its angular speed w and linear speed v both change with time. At any instant, v, ω and r are related by
v = ω r
The angular acceleration of the particle is
α = \(\frac{dω}{dt}\)
The tangential acceleration \(\vec{a_t}\) is the linear acceleration that produces a change in the linear speed of the particle and is tangent to the circle. In magnitude,
\(a_t = \frac{dv}{dt}=\frac{d}{dt}(ω r)\) ……. ( .. r is constant)
∴ \(a_t = αr\)
This is the required relation.
(ii) since \(\vec{α}\) is perpendicular to r .
Also, \(\vec{ω} × \vec{v}\) is along the radius towards the centre of the circle, i.e., opposite to \(\vec{r}\) , this acceleration is called the radial or centripetal acceleration \(\vec{a_r}\)
\(\vec{a_r}=\vec{ω}× \vec{v}\)
In magnitude, \(a_r=ω×v\)
since \(\vec{ω}\) is perpendicular to . \(\vec{v}\)
∴\(\vec{a}=\vec{a_t}+\vec{a_r} \)
This is the required expression for the resultant acceleration of a particle in terms of tangential and radial components.
| In a nonuniform circular motion, the angular acceleration is an axial vector, perpendicular to the plane of the motion. The linear acceleration is in the plane of the motion. Hence, the angle between them is 90°. |
Differences between a nonuniform circular motion and a uniform circular motion: Nonuniform circular motion : (i) The angular and tangential accelerations are non-zero, so that linear and angular speeds both change with time. \(\vec{α} =\frac{\vec{dω}}{dt}\) and \(\vec{a_t} =\frac{\vec{dv}}{dt}=\vec{α}×\vec{r}\) If a particle in nonuniform circular motion is speeding up, \(\vec{α}\) is in the direction of \(\vec{ω}\)and \(\vec{a_t}\) is in the direction of \(\vec{v}\) if the particle is slowing down, \(\vec{α}\) is opposite to \(\vec{ω}\) and \(\vec{a_t}\) is opposite to \(\vec{v}\) (ii) The net linear acceleration, being the resultant of the radial and tangential accelerations, is not radial.\(\vec{a}=\vec{a_t}+\vec{a_r} \) (ii) The magnitudes of the centripetal acceleration and the centripetal force are not constant. Example : Motion of the tip of a fan blade when the fan is speeding up or slowing down. Uniform circular motion : (i) The angular and tangential accelerations are zero, so that linear speed and angular velocity are constant. (ii) The net linear acceleration is radially inward, i.e., centripetal. (iii) The magnitudes of the centripetal acceleration and the centripetal force are also constant. Example : Motion of the tips of the hands of a mechanical clock.
Kinematical equations for circular motion in analogy with linear motion: For circular motion of a particle with constant angular acceleration a average angular speed, ωav = (ω0 + ω)/2 a = (ω - ω0)/t and θ - θ0 = ωav × t where ω0 and w are the initial and final angular speeds, t is the time, may the average angular speed and θ0 and θ the initial and final angular positions of the particle. Then, the angular kinematical equations for the circular motion are (in analogy with linear kinematical equations for constant linear acceleration) ω = ω0 + αt q - q0 = ω0 t + αt2 ω2 = ω02 + 2α(θ - θ0)
Centripetal force : In the uniform circular motion of a particle, the centripetal force is the force on the particle which at every instant points radially towards the centre of the circle and produces the centripetal acceleration to move the particle in its circular path.
Explanation :A uniform circular motion is an accelerated motion, with a radially inward (i.e.centripetal) acceleration \(\frac{-v}{r}\breve{r}\) or — ω2 \(\vec{r}\), where \(\vec{r}\) is the radius vector and \(\breve{r}\) is a unit vector the direction of \(\vec{r}\) . Hence, a net real force must act on the particle to produce this acceleration. This force, which at every instant must point radially towards the centre of the circle, is called the centripetal force. If m is the mass of the particle, the centripetal force is or \(-m\frac{v}{r}\breve{r}\) or — mω2 \(\vec{r}\) (2) In case the angular or linear speed changes with time, as in nonuniform circular motion, the force is not purely centripetal but has a tangential component which accounts for the tangential acceleration
(1) As viewed from an inertial frame of reference, the centripetal force is necessary and sufficient for the particle to perform UCM. At any instant, if the centripetal force suddenly vanishes, the particle would fly off in the direction of its linear velocity at that instant.
Examples of centripetal force :
Centrifugal force: In the reference frame of a particle performing circular motion, centrifugal force is defined as a fictitious, radially outward force on the particle and is equal in magnitude to the particle's mass times the centripetal acceleration of the reference frame, as measured from an inertial frame of reference.
Explanation: A uniform circular motion is an accelerated motion, with a centripetal acceleration of magnitude v2/r or ω2r. A frame of reference attached to the particle also has this acceleration and, therefore, is an accelerated or noninertial reference frame. The changing direction of the linear velocity appears in this reference frame as a tendency to move radially outward. This is explained by assuming a fictitious centrifugal, i.e., radially outward, force acting on the particle. Since the particle is stationary in its reference frame, the magnitude of the centrifugal force is mv2/r or mω2r, the same as that of the centripetal force on the particle.
Examples of centrifugal force :
Q. Why centrifugal force is called a pseudo force.
A force which arises from gravitational, electromagnetic or nuclear interaction between matter is called a real force. The centrifugal force does not arise due to any of these interactions. Therefore, it is not a real force. The centrifugal force in the noninertial frame of reference of a particle in circular motion is the effect of the acceleration of the frame of reference. Therefore, it is called a pseudo or fictitious force.
Difference between centripetal force and centrifugal force.
| centripetal force | centrifugal force |
| 1-Centripetal force is the force required to provide centripetal acceleration to a particle to move it in a circular path.
2-At every instant, it is directed radially towards the centre of the circular path. 3-It is a real force arising from gravitational or electromagnetic interaction between matter. |
1-The centrifugal tendency of the particle, in its accelerated, i.e., noninertial, frame of reference, is explained by assuming a centrifugal force acting on it.
2- At every instant, it is directed radially away from the centre of the circular path. 3-It is a pseudo force since it is the effect of the acceleration of the reference frame of the revolving particle. |
| Next Part->> |
Useful links :
| Main Page : - Maharashtra Board Class 12-Physics - All chapters notes, solutions, videos, test, pdf.
Books : MSBSHSE -Class 12th Science Text Books – Chapter wise PDF for download Next Chapter :Chapter-2-Mechanical Properties of Fluids - Online Notes |
Very good 🙂🙂 l am happy l
Very nice
Excellent
😊👌👌
Mast
Very good…and very easy to understanding ….thank you 😊😊
thanks aloot its very helpful and
Best and esay notes thank you for notes
Nice am very happy for your notes 🥰
Very easy notes📝
Very helpful notes
10q for this notes it is very easy to understand once again 10q
The best
Very easy & helpful notes thank you
Best Notes and Easily Understanding __________Thank you_________