Notes-Part-3
|
Topics To Be Learn Vertical circular motion in Earth's gravity
|
Vertical circular motion : A body revolving in a vertical circle in the gravitational field of the Earth is said to perform vertical circular motion.
- A vertical circular motion controlled only by gravity is a nonuniform circular motion because the linear speed of the body does not remain constant although the motion can be periodic.
- In a controlled vertical circular motion, such as that a body attached to a rod, the linear speed of the body can be constant (including zero) so that such a motion can be uniform and periodic.
- In a nonuniform vertical circular motion, e.g., those of a small body attached to a string or the loop-the-loop maneuvers of an aircraft or motorcycle or skateboard, the body must have some minimum speed to reach the top and complete the circle. In this case, the motion is controlled only by gravity and zero speed at the top is not possible.
- However, in a controlled vertical circular motion, e.g., those of a small body attached to a rod or the giant wheel (Ferris wheel) ride, the body or the passenger seat can have zero speed at the top, i.e., the motion can be brought to a stop.
Expressions for the minimum speeds at different locations along a vertical circular motion controlled by gravity. (Using the principle of energy conservation.) :
Consider a particle of mass m attached to a string and revolved in vertical circle of radius r, At every instant of motion there are only two forces acting on the particle (a) its weight mg, vertically downwards, which is constant and
(b) the force due to the tension along the string, directed along the string and towards the centre.
Its magnitude changes periodically with time and location.
The particle may not complete the circle if the string slackens before the particle reaches at the top. This requires that the particle must have some minimum speed.
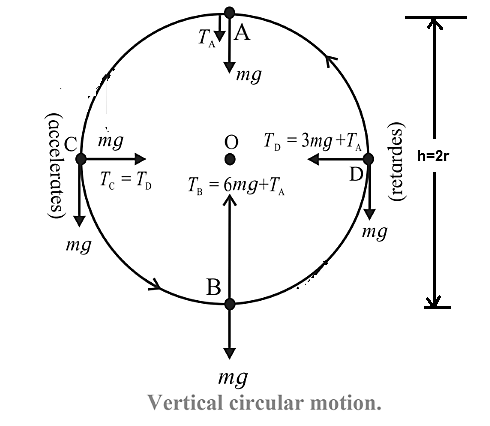
At the top position (Point A) : Let va be the speed of the particle and TA the tension in the string. Here both, weight mg and force due to tension TA are downwards, i.e. towards the centre. In this case, net force on the particle towards the center O is TA +mg is their resultant as the centripetal force.
∴ TA +mg = \(\frac{mv_A^2}{r}\) ……..(1)
For minimum possible speed at this point (or if the motion is to be realized with minimum possible energy),
TA = 0
∴ 0 + mg = \(\frac{mv_A^2}{r}\)
∴ \(\frac{mv_A^2}{r}\) = mg
That is the particle’s weight alone is the necessary centripetal force at the point A.
∴ vA2 = rg
∴ vA = \(\sqrt{rg}\) ……..(2)
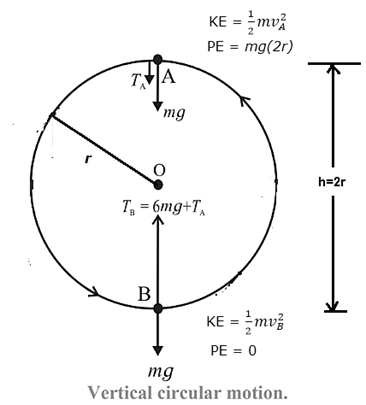
At the bottom position (Point B): Let vB The speed at bottom. Taking reference level for zero potential energy to the bottom of the circle, the particle has only kinetic energy \(\frac{1}{2}mv_B^2\) at the lowest point.
Total energy at the bottom = KE+PE
= \(\frac{1}{2}mv_B^2\) +0 = \(\frac{1}{2}mv_B^2\) …… (3)
As the particle goes from the bottom to the top of the circle, it rises through a height h=2r Therefore potential energy at top is
mgh=mg(2r) and from eq. 2 its minimum KE there is
\(\frac{1}{2}mv_A^2\) = \(\frac{1}{2}mgr\) …… (4)
Minimum Total energy at the top = KE+PE
= \(\frac{1}{2}mgr+2mgr\) = \(\frac{5}{2}mgr\)\)…… (5)
Assuming that the total energy of the particle is conserved,
Total energy at the bottom = Total energy at the top.
From eq. 4 & 5
\(\frac{1}{2}mv_B^2\) = \(\frac{5}{2}mgr\)
The minimum speed the particle must have at the bottom is
\(v_B= \sqrt{5gr}\) …….. (6)
(iii) At the midway (Point C)
Let vC be the speed at point C, so that the kinetic energy is \(\frac{1}{2}mv_C^2\)
At C the particle is at height r from the bottom of the circle.
Therefor PE at C is mgr
Total Energy at C
= \(\frac{1}{2}mv_C^2+mgr\) ……. (7)
From the law of conservation of energy total energy at C = total energy at B
∴ \(\frac{1}{2}mv_C^2+mgr\) = \(\frac{5}{2}mgr\)
∴\(v_C^2=5gr-2gr\) = 3gr
∴\(v_C=\sqrt{3gr}\)
Q. Prove that the difference between the extreme tensions (or normal forces) depends only upon the weight of the object.
Consider a small body (or particle) of mass m tied to a string and revolved in a vertical circle of radius rat a place where the acceleration due to gravity is g. At every instant of its motion, the body is acted upon by two forces, namely, its weight mg and the tension T in the string. Let vB be the speed of the body and TB be the tension in the string at the lowest point B. We take the reference level for zero potential energy to be the bottom of the circle. Then, the body has only kinetic energy \(\frac{1}{2}mv_B^2\) at the lowest point. TB = \(\frac{mv_B^2}{r}+mg\) …….(1) Total energy at the bottom is KE+PE = \(\frac{1}{2}mv_B^2\)+0 = \(\frac{1}{2}mv_B^2\) …….(2) Let vA be the speed of the body and TA be the tension in the string at the lowest point A. As the body goes from B to A it rises through a height h=2r ∴ TA = \(\frac{mv_A^2}{r}-mg\) …….(3) Total energy at A = KE+PE = \(\frac{1}{2}mv_A^2+mg(2r)\)……..(4) Then from eq. (1) and (3) TB-TA = \(\frac{mv_B^2}{r}+mg\)- \((\frac{mv_A^2}{r}-mg)\) = \(\frac{m}{r}(v_B^2-v_A^2)+2mg\)……. (5) Assuming that the total energy of the body is conserved, Total energy at the Bottom=Total energy at Top From eq. (2) and (4) \(\frac{1}{2}mv_B^2\) = \(\frac{1}{2}mv_A^2+mg(2r)\) \(v_B^2-v_A^2\) = 4gr …….(6) Substituting this in eq. (5) TB-TA = \(\frac{m}{r}(4gr)+2mg\) = 4mg+2mg = 6mg Therefore difference in the tensions in the string at the highest and the lowest point is 6 times the weight of the body.
|
Show that a vertical circular motion controlled by gravity is a nonuniform circular motion.
Consider a small body of mass m tied to a string and revolved in a vertical circle of radius r. At every instant of its motion, the body is acted upon by its weight mg and the tension T in the string. At any instant, when the body is at the position P see Fig. let the string make an angle θ with the vertical. mg is resolved into components, mg cosθ (radial) and mg sinθ (tangential).
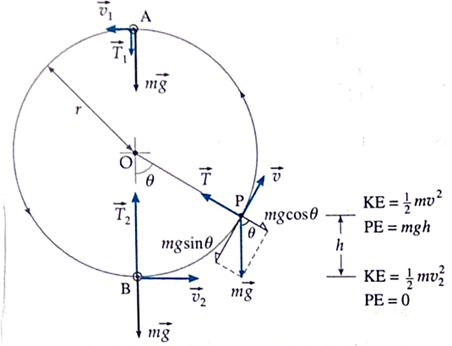
At point P shown, the net force on the body towards the centre, T— mg cosθ, is the necessary centripetal force on the body. If v is its speed at P,
T— mgcosθ = \(\frac{mv^2}{r}\)
or T = \(\frac{mv^2}{r}\) + mgcosθ ………..(1)
Let v2 be the speed of the body at the lowest point B, which is the reference level for zero potential energy. Then, the body has only kinetic energy \(\frac{1}{2}mv_2^2\) at B.
Total energy at B = KE + PE
= \(\frac{1}{2}mv_2^2\) + 0
= \(\frac{1}{2}mv_2^2\) …………..(2)
As the body goes from B to P, it rises through a height h= r — rcosθ = r(1— rcosθ)
Total energy at P = KE + PE
= \(\frac{1}{2}mv^2\) + mgh
= \(\frac{1}{2}mv^2\) + mgr(1— rcosθ) …………..(3)
Assuming that the total energy of the body is conserved, total energy at any point = total energy at the bottom.
Then, from Eqs. (2) and (3),
\(\frac{1}{2}mv^2\) + mgr(1— rcosθ) = \(\frac{1}{2}mv_2^2\)
∴ v2 = v22—2gr(1— cosθ) ………(4)
∴ v = \(\sqrt{v_2^2-2gr(1— cosθ)}\) ………..(5)
From the above expression, it can be seen that the linear speed v changes with θ. Thus, as θ increases, (while going up) cosθ decreases, 1 — cosθ increases, and v decreases. While coming down, θ decreases and v increases. Hence, a vertical circular motion controlled by gravity is a nonuniform circular motion.
Expression for the tension in the string at any instant in terms of the speed at the lowest point :
Substituting for v2 from Eq. (4) in Eq. (1),
T = \(\frac{m}{r} (v_2^2-2gr(1- cosθ))+mgcosθ\)
= \(\frac{mv_2^2}{r} -2mg+ 2mgcosθ+mgcosθ\)
= \(\frac{mv_2^2}{r} -mg(2- 3mgcosθ)\)………..(6)
This is the expression
Q. Explain clearly why the motorcyclist driving in vertical loops inside a hollow globe (sphere of death) does not fall down when at the highest point of the chamber.
A motorcyclist driving in vertical loops inside a hollow globe performs vertical circular motion. Suppose the mass of the motorcycle and motorcyclist is In and the radius of the chamber is r. At every instant of the motion, the motorcyclist is acted upon by the weight mg and the normal reaction N At the highest point, let v1 be the speed and N1 the normal reaction. Here, both N1 and mg are parallel, vertically downward. Hence, the net force on the motorcyclist towards the centre O is N1 + mg. If this force is able to provide the necessary centripetal force at the highest point, the motorcycle does not lose contact with the globe and fall down. The minimum value of this force is found from limiting case when N1, just becomes zero and weight alone provides the necessary centripetal force : \(\frac{mv_1^2}{r}\)=mg This requires that the motorcycle has a minimum speed at the highest point given by or \(v_1^2=gr\) or \(v_1=\sqrt{gr}\)
[The ‘globe of death’ is a stunt in which stunt drivers ride motorcycles inside a mesh global. Starting from small horizontal circles, they eventually perform revolutions along vertical circles. The linear speed is more for larger circles but angular speed is more for smaller circles as in conical pendulum.]
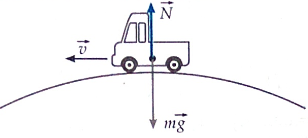
Vehicle at the Top of a Convex Over-Bridge:
Q.A car crosses over a bridge which is in the form of a convex arc with a uniform speed.
(i) State expression for the normal reaction on the car. How does the normal reaction on the car vary with speed ?
(ii) Hence show that the maximum speed with which the car can cross the bridge without losing contact with the road is equal to \(\sqrt{gr}\)
Figure shows a vehicle at the top of a convex over bridge, during its motion (part of vertical circular motion). Suppose a car of mass m, travelling with a uniform speed v, crosses over a bridge which is in the form of a convex arc of radius r. Forces acting on the vehicle are (a) Weight mg and (b) Normal reaction force N, both along the vertical line (topmost position). The resultant of these two must provide the necessary centripetal force (vertically downwards) if the vehicle is at the uppermost position. Thus, if v is the speed at the uppermost point, mg - N = mv2/r ∴ \(N=m(g-\frac{v^2}{r})\) As the speed is increased, N goes on decreasing. Normal reaction is an indication of contact. Thus, for just maintaining contact, N = 0. This imposes an upper limit on the speed as vmax = \(\sqrt{gr}\) Therefore, this is the maximum speed with which a car can cross the bridge, irrespective of its mass.
| <<-Previous Part | Next part->> |