Rotational Dynamics
Class-12th-Physics-Chapter-1-Maharashtra Board
Notes-Part-4
|
Topics To Be Learn : Moment of a inertia (MI)
Radius of gyration Theorems of parallel axis and perpendicular axes Angular momentum Expression for torque (in terms of MI) Conservation of angular momentum Rolling motion. |
Moment of inertia (MI), Kinetic energy of a rotating body :
Moment of inertia : The moment of inertia of a body about a given axis of rotation is defined as the sum of the products of the masses of the particles of the body and the squares of their respective distances from the axis of rotation.
If the body is made up of N discrete particles of masses m1, m2, ..., mN situated at respective distances r1, r2, ……., rN, from the axis of rotation, the moment of inertia of the body is
I = \(m_1r_1^2+m_2r_2^2+........m_Nr_N^2\)
= \(\sum \limits_{i=1}^{N}m_ir_i^2\) ………. (1)
For a rigid body, having a continuous and uniform distribution of mass, the moment of inertia is
I = \(\int r^2dm\)………. (2)
where dm is the mass of an infinitesimal element, situated at distance r from the axis of rotation.
The moment of inertia of a rigid body depends on
(i) the mass and shape of the body (ii) orientation and position of the rotation axis (iii) distribution of the mass about the rotation axis.
Dimensions :
[Moment of inertia] = [mass] [distance]2
= [M] [L2] = [M1L2T°]
SI unit : The kilogram-metre2 (kg-m2).
Q. Derive an expression for the kinetic energy of a body rotating with constant angular velocity :
Consider a rigid body rotating with a constant angular velocity \(\vec{ω}\); about an axis passing through the point O and perpendicular to the plane of the figure.
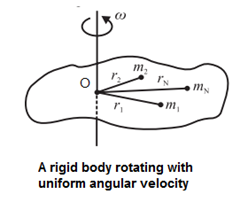
Suppose that the body is made up of N particles of masses m1, m2, ..., mN situated at perpendicular distances r1, r2, ……., rN, respectively, from the axis of rotation as shown in Fig.
As the body rotates, all the particles perform uniform circular motion with the same angular velocity ;. However, they have different linear speeds depending upon their distances from the axis of rotation.
The linear speed of the particle with mass m1 is v1= r1ω Therefore, its kinetic energy is
∴ E1 = \(\frac{1}{2}m_1v_1^2=\frac{1}{2}m_1r_1^2ω_1^2\) = ………(1)
Similarly, the kinetic energy of the particle with mass m2 is E2 = \(\frac{1}{2}m_2v_2^2=\frac{1}{2}m_2r_2^2ω_2^2\) and so on.
The rotational kinetic energy of the body is
Erot = E1+ E2 + ... + EN
= \(\frac{1}{2}m_1r_1^2ω_1^2+\frac{1}{2}m_2r_2^2ω_2^2+....\frac{1}{2}m_Nr_N^2ω_N^2\)
= \(\frac{1}{2}(m_1r_1^2ω_1^2+m_2r_2^2ω_2^2+....m_Nr_N^2ω_N^2)\)
= \(\frac{1}{2}(\sum \limits_{i=1}^{N}m_ir_i^2)ω^2\)
∴ Erot = I ω2 ……….(2)
Where I = is the moment of inertia of the body about the axis of rotation.
Equation (2) gives the required expression.
If f is the frequency of rotation of the body and T the period of rotation, then
ω =2πf = 2π/T
∴ Erot =\(\frac{1}{2}I(2πf)^2=2π^2If^2=2π^2\frac{I}{T^2}\) ……….(3)
Thus, from Eqs. (2) and (3), the rotational kinetic energy of a body is proportional to
- its moment of inertia about the given rotation axis
- the square of its angular speed (or frequency of rotation) or inverse square of its rotational period.
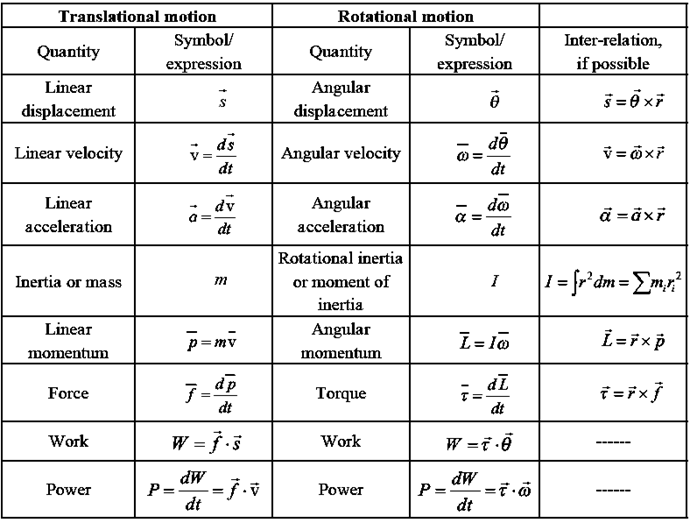
Physical significance of moment of inertia : The physical significance of moment of inertia can be understood by comparing the formulae in the following table.
| Linear motion | Rotational motion |
| 1. Momentum = mass X velocity
2. Force = mass X acceleration 3. Kinetic energy = ½ mv2 |
1.Angular momentum = moment of inertia X angular velocity
2.Torque = moment of inertia X angular acceleration 3.Kinetic energy = ½ Iω2 |
- Force produces acceleration, while torque produces angular acceleration. Force and torque are analogous quantities. Also, momentum and angular momentum are analogous quantities.
- By comparing the above formulae, we find that moment of inertia plays the same role in rotational motion as that played by mass in linear motion. The moment of inertia of a body is its rotational inertia, that which opposes any tendency to change its angular velocity. In the absence of a net torque, the body continues to rotate with a uniform angular velocity.
Q. Three point masses M1, M2 and M3 are located at the vertices of an equilateral triangle of side a. What is the moment of inertia of the system about an axis along the altitude of the triangle passing through M1?
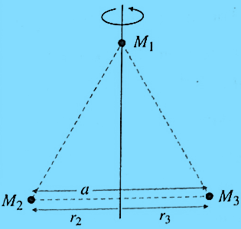
The moment of inertia of the system about the altitude passing through M1, is
I = \(M_1r_1^2+M_2r_2^2+M_3r_3^2\)
Since M1 lies on the axis of rotation, r1 = 0.
Also, r2=r3=a/2.
∴ I = (M2+M3)\((\frac{a}{2})^2\) =\(\frac{1}{4}\)(M2+M3)a2
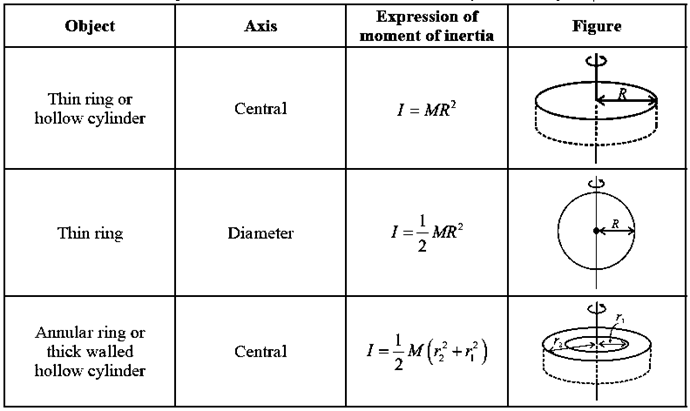
Expression for the moment of inertia of a thin ring about its transverse symmetry axis :
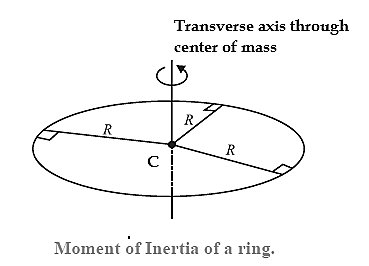
A thin uniform ring (or hoop) has all it’s mass uniformly distributed along the circumference of a circle, IL is taken to be a two-dimensional body. It is also assumed that the radial thickness of the ring is so small as to be completely negligible in comparison to its radius.
If it is rotating about its own axis (line perpendicular to its plane and passing through its centre C, its entire mass M is practically at a distance equal to its radius R form the axis. Hence, the expression for the moment of inertia of a uniform ring of mass M and radius R is
I = MR2
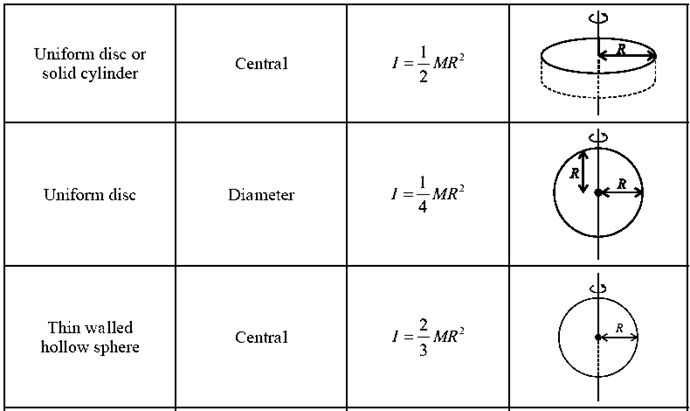
Moment of inertia of a thin uniform disc :
A thin uniform disc has all its mass homogeneously distributed over its circular surface area. It is taken to be a two-dimensional body, i.e., its axial thickness is small as to be completely negligible in comparison to its radius. Consider a thin disc of radius R and mass M. Its mass per unit area is
σ = M/A = \(\frac{M}{πR^2}\) ............(1)
The axis of rotation is the transverse symmetry axis, through its centre of mass (CM) and perpendicular to its plane. As it is a uniform circular object, it can be considered to be consisting of a number of concentric rings of radii increasing from (practically) zero to R. One of such rings of mass dm is shown by shaded portion in the Fig.
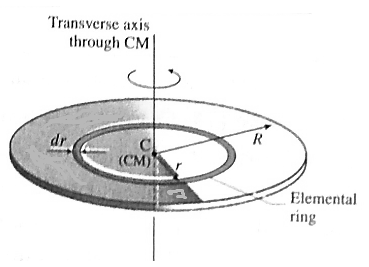
Width of this ring is dr, which is so small that the entire ring can be considered to be of average radius r. (In practical sense, dr is less than the least count of the instrument that measures r, so that r is constant for that ring).
Since the disc is uniform, the area and mass of this elemental ring are
A = 2πr.dr and dm = 2πσr.dr (… σ = dm/A = dm/ 2πr.dr ) ……. (2)
and its moment of inertia (MI) about the given axis is dm.r2.
Therefore, the MI of the disc is
I = \(\int \limits_{0}^{R}r^2dm = \int \limits_{0}^{R}r^2(2πσr.dr)=2πσ \int \limits_{0}^{R}r^3dr\)……. (3)
I = 2πσ \(\frac{R^4}{4}\) = 2π\((\frac{M}{πR^2})(\frac{R^4}{4})=\frac{1}{2}MR^2\)……. (3)
This gives the required expression
Radius of gyration : The radius of gyration of a body rotating about an axis is defined as the distance between the axis of rotation and the point at which the entire mass of the body can be supposed to be concentrated so as to give the same moment of inertia as that of the body about the given axis.
The moment of inertia (MI) of a body about a given rotation axis depends upon (i) the mass of the body and (ii) the distribution of mass about the axis of rotation. These two factors can be separated by expressing the MI as the product of the mass (M) and the square of a particular distance (k) from the axis of rotation. This distance is called the radius of gyration and is defined as given above. Thus,
\(I=\sum \limits_{i}m_ir_i^2=Mk^2\)
∴ \(k=\frac{I}{M}\)
Physical significance : The radius of gyration is less if I is less, i.e., if the mass is distributed close to the axis; and it is more if I is more, i.e., if the mass is distributed away from the axis. Thus, it gives the idea about the distribution of mass about the axis of rotation.
- Radius of gyration of a rigid body depends on the distribution of mass of the body about a rotation axis and, therefore, changes with the choice of the rotation axis. Hence, unlike the mass of the body which is constant, radius of gyration and moment of inertia of the body are not constant.
Q. Can you find some similarity between the centre of mass and radius of gyration?
The centre of mass (CM) coordinates locates a point where if the entire mass M of a system of particles or that of a rigid body can be thought to be concentrated such that the acceleration of this point mass obeys Newton's second law of motion, viz.
F = Ma, where F is the sum of all the external forces acting on the body or on the individual particles of the system of particles.
Similarly, radius of gyration locates a point from the axis of rotation where the entire mass M can be thought to be concentrated such that the angular acceleration of that point mass about the axis of rotation obeys the relation, τnet = Mα where τnet is the sum of all the external torques acting on the body or on the individual particles of the system of particles.
Q. Show that for rotation about respective transvers symmetry axis, the radius of gyration of a thin disc is less than that of a thin ring.
The MI of the ring about the transverse symmetry axis is
I = MR2 ………….(1)
The radius of gyration of the ring about the transverse symmetry axis is
k = \(\sqrt{\frac{I}{M}}=\sqrt{R^2}\) = R ………….(2)
The MI of the disc about the transverse symmetry axis is
I= ½MR2 …….(3)
The radius of gyration of the disc for the given rotation axis is
k = \(\sqrt{\frac{I}{M}}=\sqrt{\frac{R^2}{2}}=R\frac{1}{\sqrt{2}}\)…….(4)
Therefore, k(disc) < k(ring)
If a uniform ring and a uniform disc have the same radius of gyration :
The radius of gyration of a thin ring of radius Rr about its transverse symmetry axis is
kr = \(\sqrt{\frac{I}{M}}=\sqrt{R_r^2}\)= Rr
The radius of gyration of a thin disc of radius Rd about its transverse symmetry axis is
kd = \(\sqrt{\frac{I}{M}}=\sqrt{\frac{R_d^2}{2}}=R_d\frac{1}{\sqrt{2}}\)
Given kr = kd,
∴ Rr = \(R_d\frac{1}{\sqrt{2}}\) or Rd = \(\sqrt{2}\)Rr
Theorem of parallel axis : The moment of inertia of a body about an axis is equal to the sum of (i) its moment of inertia about a parallel axis through its centre of mass and (ii) the product of the mass of the body and the square of the distance between the two axes.
Proof : Figure shows an object of mass M.
Axis MOP is any axis passing through point O.
Axis ACB is passing through the centre of mass C of the object, parallel to the axis
MOP, and at a distance h from it (∴ h = CO).
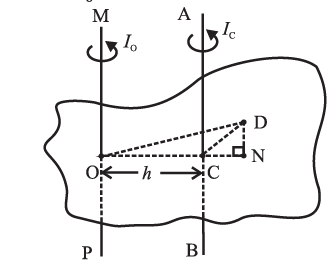
Consider a mass element dm located at point D.
Perpendicular on OC (produced) from point D is DN.
Moment of inertia of the object about the axis ACB is
IC = \(\int (DC)^2dm\)
and about the axis MOP it is
∴ IO = \(\int (DO)^2dm\)
IO = \(\int (DO)^2dm\) = \(\int [(DN)^2+(NO)^2]dm\)
= \(\int [(DN)^2+(NC)^2+2OC•CN+(OC)^2]dm\)
= \(\int [(DC)^2+2h•CN+(h)^2]dm\)
Now, \(\int (DC)^2dm\) = IC and \(\int dm\) = M
CN is the distance of a point from the centre of mass. Any mass distribution is symmetric about the centre of mass. Thus, from the definition of the centre of mass,
\(\int CNdm\) =0
∴ IO = IC + Mh2
This is the mathematical form of the theorem of parallel axes.
It states that, “The moment of inertia (IO) of an object about any axis is the sum of its moment of inertia (IC) about an axis parallel to the given axis, and passing through the centre of mass and the product of the mass of the object and the square of the distance between the two axes (Mh2).”
| The theorem of parallel axis is applicable to any body of arbitrary shape. The moment of inertia (MI) of the body about an axis through the centre mass should be known, say, ICM. Then, the theorem can be used to find the MI, I, of the body about an axis parallel to the above axis. If the distance between the two axes is h,
∴ I = ICM + Mh2 |
Theorem of perpendicular axes : The moment of inertia of a plane lamina about an axis perpendicular to its plane is equal to the sum of its moments of inertia about two mutually perpendicular axes in its plane and through the point of intersection of the perpendicular axis and the lamina.
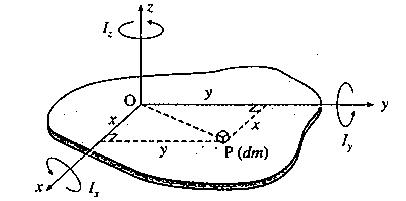
Proof : Let Ox and Oy be two perpendicular axes in the plane of the lamina and Oz, an axis perpendicular to its plane.
Consider an infinitesimal mass element dm of the lamina at the point P(x, y). MI of the lamina about the z-axis,
IZ = \(\int (OP)^2dm\)
The element is at perpendicular distance y and x from the x- and y- axes respectively.
Hence, the moments of inertia of the lamina about the x- and y-axes are, respectively,
Ix = \(\int y^2dm\) and Iy = \(\int x^2dm\)
Since OP2 = y2 + x2,
Iz = \(\int (OP)^2dm\) = \(\int (y^2+x^2)dm\)
= \(\int y^2dm + \int x^2dm\)
∴ Iz = Ix + Iy
This proves the theorem of perpendicular axes.
| The theorem of perpendicular axes is applicable to a plane lamina only. The moment of inertia of a plane lamina about an axis—the z axis perpendicular to its plane is equal to the sum of its moments of inertia Ix, and Iy about two mutual perpendicular axes x and y in its plane and through the point of intersection of the perpendicular axis and the lamina.
Iz = Ix + Iy |
Q. About which axis of rotation is the radius of gyration of a body the least?
Ans. The radius of gyration of a body is the least about an axis through the centre of mass (CM) of the body.
From the parallel axis theorem, we know that given body has the smallest possible moment of inertia about an axis through its CM. The radius of gyration of a body about a given axis is directly proportional to the square root of its moment inertia about that axis. Hence, the conclusion.
l = ICM+Mh2. ∴ Mk2 = Mk2CM + Mh2.
∴ k2 = k2CM + h2 ………. which shows that k is minimum equal to kCM when h = 0.
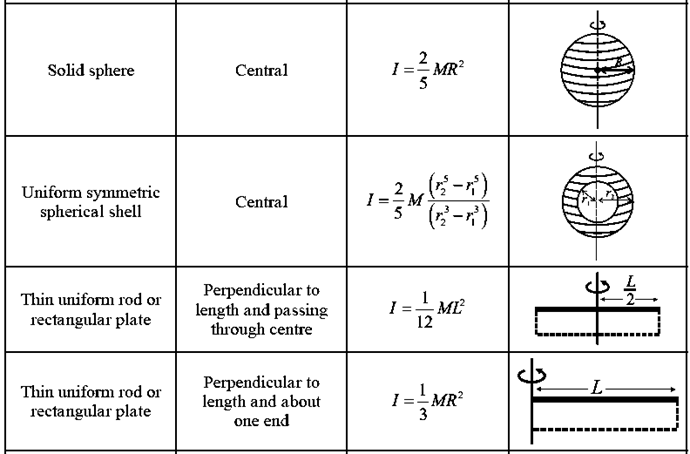
Moment of inertia a thin uniform rod :
MI about a transverse axis through centre : Consider a thin uniform rod AB of mass M and length L, rotating about a transverse axis through its centre C, see Fig. C is also its centre of mass (CM).
The moment of inertia (MI) of the rod about a transverse axis through C is
ICM = \(\frac{ML^2}{12}\) ……….. (1)
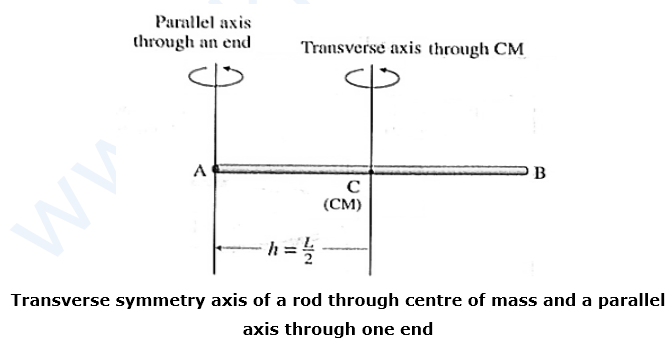
MI about a transverse axis through one end : Let I be its MI about a transverse axis through its end A.
We know that by the theorem of parallel axis,
I = ICM + Mh2 ……….. (2)
In this case,
h = distance between the parallel axes = L/2
∴ I = \(\frac{ML^2}{12} + M(\frac{L}{2})^2\)
= \(\frac{ML^2}{12} + \frac{ML^2}{4}\)
= \(\frac{ML^2}{3}\) ……….. (3)
Radii of gyration : The radius of gyration of the rod about its transverse symmetry axis is
k = \(\sqrt{\frac{I_{CM}}{M}}\) = \(\sqrt{\frac{L^2}{12}}\) = \(\frac{L}{2\sqrt{3}}\)……….. (4)
The radius of gyration of the rod about the transverse axis through an end is
k = \(\sqrt{\frac{I}{M}}\) = \(\sqrt{\frac{L^2}{3}}\) = \(\frac{L}{\sqrt{3}}\) ……….. (5)
State an expression for the moment of inertia of a thin ring about its tangential axis perpendicular to its plane Also deduce the expression for the corresponding radius of gyration.
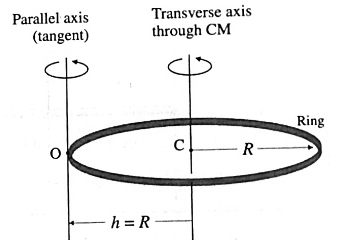
We know that the MI of the ring about the transverse symmetry axis is
ICM = MR2. …….. (1)
∴ The radius of gyration of the ring about the transverse symmetry axis is
k = \(\sqrt{\frac{I_{CM}}{M}}=\sqrt{R^2}=R\) …………..(2)
MI about a tangent perpendicular to its plane : Let I be its MI about a parallel axis, tangent to the ring.
Here, h = R = distance between the two axes.
By the theorem of parallel axis,
I=ICM+Mh2 ………………(3)
= MR2 + MR2 = 2MR2 ………………..(4)
Radius of gyration :
∴ The radius of gyration of the ring about a transverse tangent is
k = \(\sqrt{\frac{I}{M}}=\sqrt{2R^2}=\sqrt{2}R\)……………….(5)
Expression for the moment of inertia of a thin ring about its diameter :
MI about a diameter : Let x- and y-axes be along two perpendicular diameters of the ring as shown in Fig. Let Ix, Iy and IZ be the moments of inertia of the ring about the x, y and z axes, respectively.
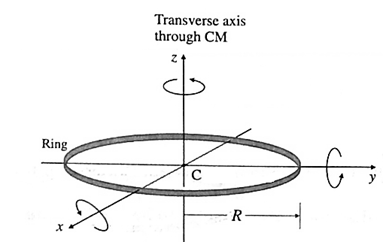
Both Ix, and Iy represent the moment of inertia of the ring about its diameter and, by symmetry, the MI of the ring about any diameter is the same.
Ix =Iy …………….(2)
Also, IZ being the MI of the ring about its transverse symmetry axis,
IZ = ICM = MR2 ………………(3)
By the theorem of perpendicular axes,
IZ = Ix + Iy = 2Ix ………….(4)
2Ix = MR2
Or Ix = MR2/2
Radius of gyration : The radius of gyration of the ring for rotation about its diameter is
k = \(\sqrt{\frac{I}{M}}=\sqrt{\frac{R^2}{2}}=\frac{R}{\sqrt{2}}\)………….(6)
Ml of a thin ring about a tangent in its plane :
Let I be its MI about an axis in plane of the ring, i.e., parallel to a diameter, and tangent to it. Here, h =R and
ICM = Ix = MR2/2
By the theorem of parallel axis,
I = Ix+Mh2
= ½MR2+MR2 = \(\frac{3}{2}\)MR2 ……………(7)
Radius of gyration : The radius of gyration of the ring for rotation about a tangent in its plane
k = \(\sqrt{\frac{I}{M}}=\sqrt{\frac{3R^2}{2}}=\sqrt{\frac{3}{2}}R\)………….(8)
Angular momentum
The angular momentum of a particle is defined as the moment of the linear momentum of the particle.
It is similar to the torque being moment of a force.
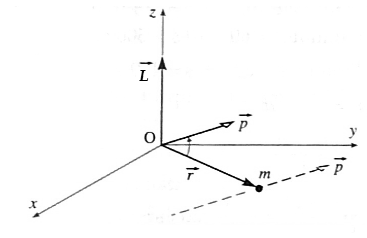
If \(\vec{p}\) (= \(m\vec{v}\)) is the instantaneous linear momentum of a particle undertaking a circular motion, its angular momentum at that instance is given by \(\vec{L}\)= \(\vec{r}×\vec{p}\) = m(\(\vec{r}×\vec{v})\), where \(\vec{r}\) is the position vector from the axis of rotation.
In magnitude, it is the product of linear momentum and its perpendicular distance from the axis of rotation. It is the angular analogue of linear momentum
∴ L = P × r sinθ , where θ is the smaller angle between the directions of \(\vec{p}\) and \(\vec{r}\)
.Dimensions : [Angular momentum] = [M1L2T-1]
SI Unit : The kilogram-metre2/ second (kg-m2/s).
Expression for Angular Momentum in Terms of Moment of Inertia:
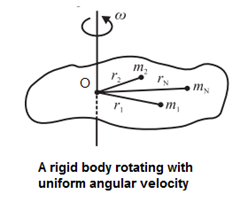
Figure shows a rigid object rotating with a constant angular speed ω about an axis perpendicular to the plane of paper.
For theoretical simplification let us consider the object to be consisting of N number of particles of masses m1, m2, ….. mN at respective perpendicular distances r1, r2, …..rN from the axis of rotation.
As the object rotates, all these particles perform UCM with same angular speed ω , but with different linear speeds v1 = r1 ω , v2 = r2 ω , ..... vN = rN ω
Directions of individual velocities \(\vec{v_1},\vec{v_2}\) etc., are along the tangents to their respective tracks.
Linear momentum of the first particle is of magnitude p1 = m1 v1 = m1r1 ω .
Its direction is along that of v1
Its angular momentum is thus of magnitude L1 = p1 r1 = m1r12 ω
Similarly, L2 = m2r22 ω , L3 = m3r32 ω ……….. LN = mNrN2 ω
For a rigid body with a fixed axis of rotation, all these angular momenta are directed along the axis of rotation, and this direction can be obtained by using right hand thumb rule.
As all of them have the same direction, their magnitudes can be algebraically added.
Thus, magnitude of angular momentum of the body is given by
L = m1r12 ω + m2r22 ω + m3r32 ω + ……….. + mNrN2 ω
= (m1r12 + m2r22 + m3r32 + ……….. + mNrN2 )ω = I ω
Where, I = m1r12 + m2r22 + m3r32 + ……….. + mNrN2 is the moment of inertia of the body about the given axis of rotation.
Thus, angular momentum = moment of inertia X angular velocity
The expression for angular momentum L = Iω is analogous to the expression p = mv of linear momentum, if the moment of inertia I replaces mass, which is its physical significance.
Kinetic energy of a rotating body in terms of its angular momentum :
The kinetic energy of a body of moment of inertia I and rotating with a constant angular velocity ω is
E = ½ Iω2
The angular momentum of the body, L = Iω.
E = ½ (Iω)ω= ½ Lω
This is the required relation.
Q. Why do grinding wheels have large mass and moderate diameter?
Expression for torque (in terms of MI) :
A torque acting on a body produces angular acceleration.
Consider a rigid body rotating about an axis passing through the point O and perpendicular to the plane of the figure. Suppose that a torque \(\vec{τ}\) on the body produces uniform angular acceleration \(\vec{α}\) along the axis of rotation.
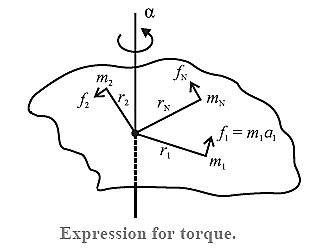
The body can be considered as made up of N particles with masses m1, m2, ….. mN situated at perpendicular distances r1, r2, …..rN respectively from the axis of rotation \(\vec{α}\) is the same for all the particles as the body is rigid. Let f1, f2, …..fN be the external forces on the particles.
Thus, the torque experienced by the first particle is of magnitude τ1 = f1 r1 = m1 r12α
Similarly, τ2 = m2 r22α , τ3 = m3 r32α ………. τN = mN rN2α
If the rotation is restricted to a single plane, directions of all these torques are the same, and along the axis. Magnitude of the resultant torque is then given by
τ = τ1+ τ2 + τ3 +………..+ τN
= (m1r12 + m2r22 + m3r32 + ……….. + mNrN2 ) α = I α
Where, I = m1r12 + m2r22 + m3r32 + ……….. + mNrN2 is the moment of inertia of the body about the given axis of rotation.
In vector form, \(\vec{τ}\) = \(I\vec{α}\)
This gives the required relation.
Angular acceleration has the same direction as the torque and both of them are axial vectors along the rotation axis.
The relation I = I α is analogous to f = ma for the translational motion if the moment of inertia I replaces mass, which is its physical significance.
Conservation of Angular Momentum :
Principle (or law) of conservation of angular momentum : The angular momentum of a body is conserved if the resultant external torque on the body is zero.
Proof : Consider a moving particle of mass m whose position vector with respect to the origin at any instant is \(\vec{r}\)
Then, at this instant, the linear velocity of this particle is \(\vec{v}=\frac{d\vec{r}}{dt}\) , its linear momentum is \(\vec{p}=m\vec{v}\) and its angular momentum about an axis through the origin is (\vec{l}=\vec{r}×\vec{p}\) .
Suppose its angular momentum (\vec{l}\) changes with time due to a torque exerted on the particle.
The time rate of change of its angular momentum,
\(\frac{d\vec{l}}{dt}=\frac{d}{dt}(\vec{r}×\vec{p})\)=\(\frac{d\vec{r}}{dt}×\vec{p}+\vec{r}×\frac{d\vec{p}}{dt}\)
=\(\vec{v}×m\vec{v}+\vec{r}×\vec{F}\)
= \(\vec{r}×\vec{F}\) ….(‘.’ \(\vec{v}×\vec{v}=0\))
= \(\vec{τ}\)
where \(\frac{d\vec{p}}{dt}=\vec{F}\), the net force on the particle.
Hence, if \(\vec{τ}=0\), \(\frac{d\vec{l}}{dt}=0\)
\(\vec{l}\) = constant, i.e.,\(\vec{l}\) is conserved. This proves the principle (or law) of conservation of angular momentum.
Examples of conservation of angular momentum:
This law (or principle) is used by a figure skater or a ballerina to increase their speed of rotation for a spin by reducing the body's moment of inertia. A diver too uses it during a somersault for the same reason.
(i) Ballet dancers: During ice ballet, the dancers have to undertake rounds of smaller and larger radii. The dancers come together while taking the rounds of smaller radius (near the centre). In this case, the moment of inertia of their system becomes minimum and the frequency increases, to make it thrilling. While outer rounds, the dancers outstretch their legs and arms. This increases their moment of inertia that reduces the angular speed and hence the linear speed. This is essential to prevent slipping.

(ii) Diving in a swimming pool (during competition): While on the diving board, the divers stretch their body so as to increase the moment of inertia. Immediately after leaving the board, they fold their body. This reduces the moment inertia considerably. As a result, the frequency increases and they can complete more rounds in air to make the show attractive.
Again, while entering into water they stretch their body into a streamline shape. This allows them a smooth entry into the water.
- In all these applications the product L = Iω = I(2πn) is constant (once the players acquire a certain speed). Thus, if the moment of inertia I is increased, the angular speed and hence the frequency of revolution n decreases. Also, if the moment of inertia is decreased, the frequency increases.
Q. Fly wheels used in automobiles and steam engines producing rotational motion have discs with a large moment of inertia. Explain why?
Ans. A flywheel is used as
- a mechanical energy storage, the energy being stored in the form of rotational kinetic energy
- a direction and speed stabilizer. A flywheel rotor is typically in the form of a disc.
Rotational kinetic energy, Erot = \(\frac{1}{2}Iω^2\)
where I is the moment of inertia and ω is the angular speed. That is, Erot ∝ I. Therefore, higher the moment of inertia, the higher is the rotational kinetic energy that can be stored or recovered.
Also, angular momentum, \(\vec{L}=I\vec{ω}\), i.e., \(|\vec{L}| ∝ I\).
A torque aligned with the symmetry axis of a flywheel can change its angular velocity and there-by its angular momentum. A flywheel with a large angular momentum will require a greater torque to change its angular velocity. Thus, a flywheel can be used to stabilize direction and magnitude of its angular velocity by undesired torques.
Rolling Motion:
Two motions of pure rolling : In the case of pure rolling, two motions are undertaking simultaneously; circular motion and linear motion.
Consider a circularly symmetric rigid body, like a wheel or a disc, rolling on a plane surface with friction along a straight path.
The centre of mass of the wheel is at its geometric centre O. For purely translational motion (the wheel sliding smoothly along the surface without rotating at all), every point on the wheel has the same linear velocity \\vec{v}_{CM}=\vec{v}_O\) as the centre O.
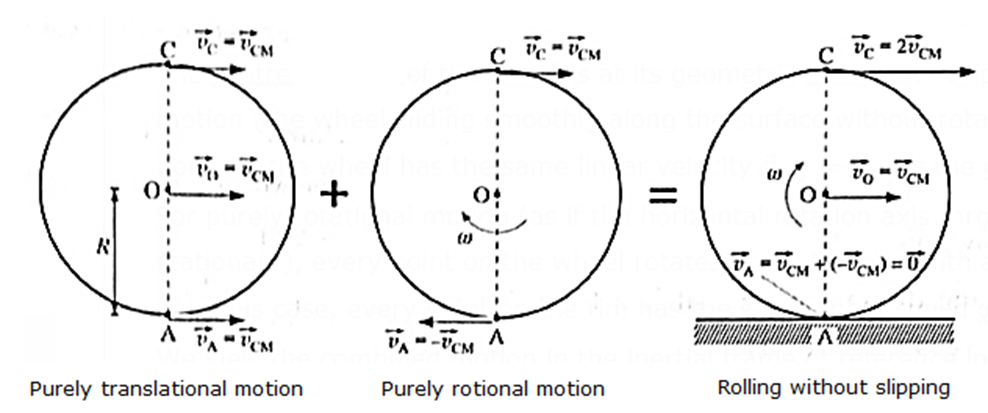
For purely rotational motion (as if the horizontal rotation axis through O were stationary), every point on the wheel rotates about the axis with angular velocity
in this case, every point on the rim has the same linear speed ωR.
We view the combined motion in the inertial frame of reference in which the surface is at rest. In this frame, since there is no slipping, the point of contact of the wheel with the surface is instantaneously stationary, vA = 0, so that the wheel is turning about an instantaneous axis through the point of contact A.
The instantaneous linear speed of point C (at the top) is vC = ω(2R) faster than any other point of the wheel.
Expression for the kinetic energy of a body rolling on a plane surface without slipping :
Consider a symmetric rigid body, like a sphere or a wheel or a disc, rolling on a plane surface with friction along a straight path. Its centre of mass (CM) moves in a straight line and, if the frictional force on the body is large enough, the body rolls without slipping. Thus, the rolling motion of the body can be treated as translation of the CM and rotation about an axis through the CM.
Hence, the kinetic energy of a rolling body is E = Etran + Erot …..(1)
where Etran, and Erot, are the kinetic energies associated with translation of the CM and rotation about an axis through the CM, respectively.
Let M and R be the mass and radius of the body.
Let ω, k and I be the angular speed, radius of gyration and moment of inertia for rotation about an axis through its centre, and v be the translational speed of the centre of mass.
∴ v = ωR and I = Mk2 …..(2)
∴ Etran = \(\frac{1}{2}\)Mv2 and Erot = \(\frac{1}{2}\)Iω2 …..(3)
∴ E = \(\frac{1}{2}\)Mv2 + \(\frac{1}{2}\)Iω2 = \(\frac{1}{2}\)Mv2 + \(\frac{1}{2}I\frac{v^2}{R^2}\)
= \(\frac{1}{2}\)Mv2\((1+\frac{I}{MR^2})\) …..(4)
= \(\frac{1}{2}\)Mv2\((1+\frac{Mk^2}{MR^2})\)= \(\frac{1}{2}\)Mv2\((1+\frac{k^2}{R^2})\) …..(5)
From eq.(2)
E = \(\frac{1}{2}\)Mω2R2 \([1+\frac{k^2}{R^2}]\)= \(\frac{1}{2}\)Mω2(R2 + k2) …..(6)
Equation (4) or (5) or (6) gives the required expression.
Kinetic energy of a solid sphere :
For solid sphere k =\(\sqrt{2/5}R\) so that I = \(\frac{2}{5}\)MR2
∴ \(\frac{I}{MR^2}=\frac{2}{5}\) …..(7)
Substituting in eq. (4)
E = \(\frac{1}{2}\)Mv2\([1+\frac{2}{5}]\) = \(\frac{1}{2}\)Mv2\((\frac{7}{5})\) = \(\frac{7}{10}\)Mv2…..(8)
Linear Acceleration and Speed While Pure Rolling Down an Inclined Plane:
Consider a circularly symmetric rigid body, like a sphere or a wheel or a disc, rolling with friction down a plane inclined at an angle θ to the horizontal. If the frictional force on the body is large enough, the body rolls without slipping.
Let M and R be the mass and radius of the body.
Let I be the moment of inertia of the body for rotation about an axis through its centre.
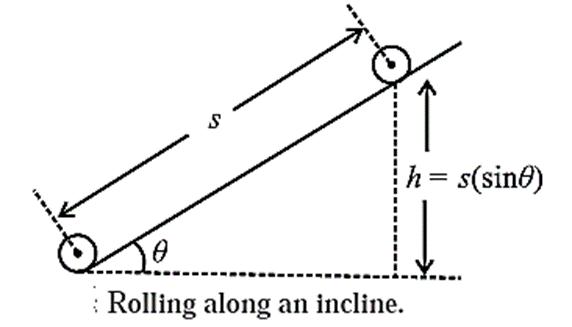
Let the body start from rest at the top of the incline at a height h.
Let v be the translational speed of the centre of mass at the bottom of the incline. Then, its kinetic energy at the bottom of the incline is
E = \(\frac{1}{2}Mv^2(1+\frac{I}{MR^2})\)…..(1)
If k is the radius of gyration of the body, I = Mk2
∴ E = \(\frac{1}{2}Mv^2(1+\frac{k^2}{R^2}\)
From conservation of energy,
(KE + PE)initial = (KE + PE)final ……(2)
∴ 0 + Mgh = \(\frac{1}{2}Mv^2(1+\frac{k^2}{R^2})\) + 0
∴ Mgh = \(\frac{1}{2}Mv^2(1+\frac{k^2}{R^2})\) ……(3)
∴ v2 = \(\frac{2gh}{1+\frac{k^2}{R^2}}\)
∴ v = \(\sqrt{\frac{2gh}{1+\frac{k^2}{R^2}}}\) ……(4)
Since h = s sin θ
v = \(\sqrt{\frac{2gs\,sin θ}{1+\frac{k^2}{R^2}}}\) ……(5)
Let a be the acceleration of the centre of mass of the body along the inclined plane. Since the body starts from rest,
v2 = 2as, ∴ a = \(\frac{v^2}{2s}\) ……(6)
∴ a = \(\frac{2gs\,sin θ}{1+\frac{k^2}{R^2}}.\frac{1}{2s}\)
= \(\frac{g\,sin θ}{1+\frac{k^2}{R^2}}\) ……(7)
Starting from rest, if t is the time taken to travel the distance s,
s = at2
∴ t = \(\sqrt{\frac{2s}{a}}\)=\(\sqrt{\frac{2s}{g\,sinθ}.(1+\frac{k^2}{R^2})}\)
Expression for the speed of Ring, solid cylinder, spherical shell and solid sphere :
We know for a circularly symmetric body, of mass M and radius of gyration k, starting from rest on an inclined plane and rolling clown without slipping
Its speed after rolling down through a height h is
v = \(\sqrt{\frac{2gh}{1+\frac{k^2}{R^2}}}\)
I = Mk2 ∴ k2 = I/M
∴ v = \(\sqrt{\frac{2gh}{1+\frac{I}{MR^2}}}\)
(i) For ring I = MR2
∴ v = \(\sqrt{\frac{2gh}{1+1}}\) = \(\sqrt{gh}\)
(ii) For solid cylinder or disc : I = \(\frac{1}{2}\)MR2
∴ v = \(\sqrt{\frac{2gh}{1+1/2}}\) = \(\sqrt{\frac{4}{3}gh}\) = \(\sqrt{1.333gh}\)
(iii) For spherical shell (hollow sphere) : I = \(\frac{2}{3}\)MR2
∴ v = \(\sqrt{\frac{2gh}{1+2/3}}\) = \(\sqrt{\frac{6}{5}gh}\) = \(\sqrt{1.2gh}\)
(iv) For solid sphere : I = \(\frac{2}{5}\)MR2
∴ v = \(\sqrt{\frac{2gh}{1+2/5}}\) = \(\sqrt{\frac{10}{7}gh}\) = \(\sqrt{1.428gh}\)
Expression for the acceleration of Ring, solid cylinder, spherical shell and solid sphere :
A circularly symmetric rigid body, of radius R and radius of gyration k, on rolling down an inclined plane of inclination θ has an acceleration
a = \(\frac{g\,sin θ}{1+\frac{k^2}{R^2}}\)=\(\frac{g\,sin θ}{1+\frac{I}{MR^2}}\) ……(as I = Mk2 ∴ k2 = I/M) ……(1)
(i) For ring I = MR2
a = \(\frac{g\,sin θ}{1+1}\) ... (= 0.5 g sin θ) ……(2)
(ii) For solid cylinder or disc : I = \(\frac{1}{2}\)MR2
a = \(\frac{g\,sin θ}{1+1/2}\) = \(\frac{2}{3}g\,sin θ\) ... (= 0.667 g sin θ) ……(3)
(iii) For spherical shell (hollow sphere) : I = \(\frac{2}{3}\)MR2
a = \(\frac{g\,sin θ}{1+2/3}\) = \(\frac{3}{5}g\,sin θ\) ...(= 0.6 g sin θ) ……(4)
(iv) For solid sphere : I = \(\frac{2}{5}\)MR2
a = \(\frac{g\,sin θ}{1+2/5}\) = \(\frac{5}{7}g\,sin θ\) (= 0.714 g sin θ) ……(5)
Note :
Equations (2), (3), (4) and (5) show that if a ring, a solid cylinder, hollow sphere and a solid sphere have exactly the same mass M and the same radius R and released simultaneously from rest at the top of an inclined plane and they roll down without slipping, then the sphere accelerates the fastest and therefore reaches the bottom first before the solid cylinder and hollow sphere, while the ring's acceleration is the least and therefore reaches last.
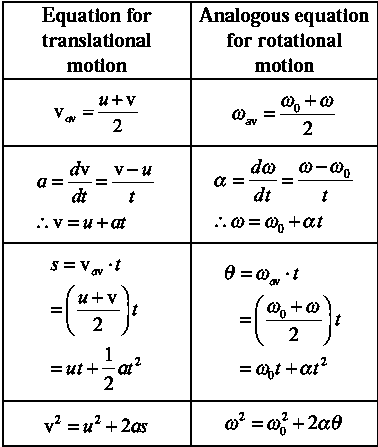
Formulae : kinematical equations (ω0 is the initial angular velocity) :
Formulae : Translational motion and rotational motion:
Formulae : Moment of inertias for some symmetric objects:
| <<-Previous Part |
Useful links :
| Main Page : - Maharashtra Board Class 12-Physics - All chapters notes, solutions, videos, test, pdf.
Books : MSBSHSE -Class 12th Science Text Books – Chapter wise PDF for download Next Chapter :Chapter-2-Mechanical Properties of Fluids - Online Notes |