Rotational Dynamics
Class-12th-Physics-Chapter-1-Maharashtra Board
Solution
Question 1.
Choose the correct option.
i) When seen from below, the blades of a ceiling fan are seen to be revolving anticlockwise and their speed is decreasing.
Select correct statement about the directions of its angular velocity and angular acceleration.
(A) Angular velocity upwards, angular acceleration downwards.
(B) Angular velocity downwards, angular acceleration upwards.
(C) Both, angular velocity and angular acceleration, upwards.
(D) Both, angular velocity and angular acceleration, downwards.
(A) Angular velocity upwards, angular acceleration downwards.
ii) A particle of mass 1 kg, tied to a 1.2 m long string is whirled to perform vertical circular motion, under gravity. Minimum speed of a particle is 5 m/s. Consider following statements.
P) Maximum speed must be 5 5 m/s.
Q) Difference between maximum and minimum tensions along the string is 60 N.
Select correct option.
(A) Only the statement P is correct.
(B) Only the statement Q is correct.
(C) Both the statements are correct.
(D) Both the statements are incorrect.
(C) Both the statements are correct.
iii) Select correct statement about the formula (expression) of moment of inertia (M.I.) in terms of mass M of the object and some of its distance parameter/s, such as R, L, etc.
(A) Different objects must have different expressions for their M.I.
(B) When rotating about their central axis, a hollow right circular cone and a disc have the same expression for the M.I.
(C) Expression for the M.I. for a parallelepiped rotating about the transverse axis passing through its centre includes its depth.
(D) Expression for M.I. of a rod and that of a plane sheet is the same about a transverse axis.
(B) When rotating about their central axis, a hollow right circular cone and a disc have the same expression for the M.I.
iv) In a certain unit, the radius of gyration of a uniform disc about its central and transverse axis is 2 5. . Its radius of gyration about a tangent in its plane (in the same unit) must be
(A) 5 (B) 2.5 (C) 2 2 5. (D) 12 5.
(B) 2.5
v) Consider following cases:
(P) A planet revolving in an elliptical orbit.
(Q) A planet revolving in a circular orbit.
Principle of conservation of angular momentum comes in force in which of these?
(A) Only for (P)
(B) Only for (Q)
(C) For both, (P) and (Q)
(D) Neither for (P), nor for (Q)
(C) For both, (P) and (Q)
ix) A thin walled hollow cylinder is rolling down an incline, without slipping. At any instant, the ratio ”Rotational K.E.:Translational K.E.: Total K.E.” is
(A) 1:1:2 (B) 1:2:3 (C) 1:1:1 (D) 2:1:3
(D) 2:1:3
Question 2
Answer in brief.
i) Why are curved roads banked?
To avoid the risk of skidding as well as to reduce the wear and tear of the car tyres, the road surface at a bend is tilted inward, i.e., the outer side of the road is raised above its inner side. This is called banking of road.
On a banked road, the resultant of the normal reaction and the gravitational force can act as the necessary centripetal force. Thus, every car can be safely driven on such a banked curve at certain optimum speed, without depending on friction. Hence, a road should be properly banked at a bend.
ii) Do we need a banked road for a two-wheeler? Explain.
- When a two-wheeler a turn along an unbanked road, the force of friction provides the centripetal force.
- The two wheeler leans inward to counteract a torque that tends to topple it outward.
- Firstly, friction cannot be relied upon to provide the necessary centripetal force on all road conditions.
- Secondly, the friction results in wear and tear of the tyres. On a banked road at a turn, any vehicle can negotiate the turn without depending on friction and without straining the tyres.
iii) On what factors does the frequency of a conical pendulum depends? Is it independent of some factors?
The frequency of conical pendulum of string length l and semi vertical angle q is
n = \(\frac{1}{2π}\sqrt[g}{L.cosθ}\)
where g is the acceleration due to gravity at the place
from above expression we can say that
(i) n ∝ \sqrt{g}
(ii) n ∝ \frac{1}{\sqrt{L}}
(iii) n ∝ \frac{1}{cosθ} ….If θ increases cosθ decreases and n increases
(iv) The frequency is independent of the mass of the bob.
iv) Why is it useful to define radius of gyration?
Radius of gyration K =\sqrt{\frac{I}{M}}
The radius of gyration is less if I is less, i.e., if the mass is distributed close to the axis; and it is more if I is more, i.e., if the mass is distributed away from the axis. Thus, it gives the idea about the distribution of mass about the axis of rotation.
v) A uniform disc and a hollow right circular cone have the same formula for their M.I., when rotating about their central axes. Why is it so?
The moment of inertia of a hollow right circular cone about its central symmetry axis is
I = (1/2)MR2,
The same as that of a disc about its transverse symmetry axis. This is because the distribution of mass of the hollow cone about its central symmetry axis is the same as that of a disc.
Question 3
While driving along an unbanked circular road, a two-wheeler rider has to lean with the vertical. Why is it so? With what angle the rider has to lean?
Derive the relevant expression. Why such a leaning is not necessary for a four wheeler?
(i) When a bicyclist takes a turn along an unbanked road, the force of friction \vec{f_s} provides the centripetal force; the normal reaction of the road \vec{N} is vertically up. If the bicyclist does not lean inward, there will be an unbalanced outward torque about the centre of gravity, fs·h, due to the friction force that will topple the bicyclist outward. The bicyclist must lean inward to counteract this torque (and not to generate a centripetal force) such that the opposite inward torque of the couple formed by and the weight g,
mg·a = fs·h1.
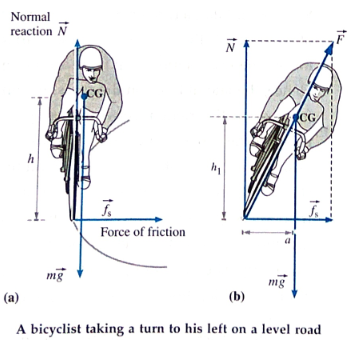
(ii) Since the force of friction provides the centripetal force,
f_s=\frac{mv^2}{r}
If the cyclist leans from the vertical by an angle q, the angle between \vec{N} and \vec{F} as shown in fig (b).
tanθ=\frac{f_s}{N}\ = \frac{mv^2/r}{mg}=\frac{v^2}{gr}
Hence, the cyclist must lean by an angle
θ =tan-1 \frac{v^2}{gr}
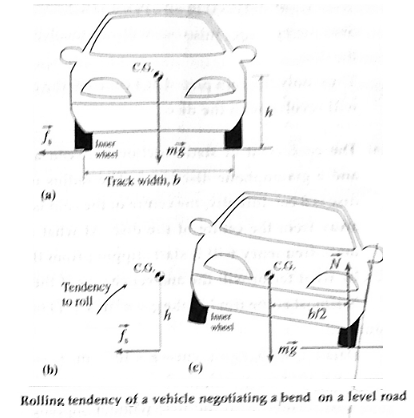
(iii) When a car takes a turn along a level road, apart from the risk of skidding off outward, it also has a tendency to roll outward due to an outward torque about the centre of gravity due to the friction force. But a car is an extended object with four wheels, So, when the inner wheels just pet lifted above the ground, it can be counterbalanced by a restoring torque of the couple formed by the normal reaction (on the outer wheels) and the weight.
Question 4
a. Using the energy conservation, derive the expressions for the minimum speeds at different locations along a vertical circular motion controlled by gravity. (4marks)
Consider a particle of mass m attached to a string and revolved in vertical circle of radius r, At every instant of motion there are only two forces acting on the particle (a) its weight mg, vertically downwards, which is constant and
(b) the force due to the tension along the string, directed along the string and towards the centre.
Its magnitude changes periodically with time and location.
The particle may not complete the circle if the string slackens before the particle reaches at the top. This requires that the particle must have some minimum speed.
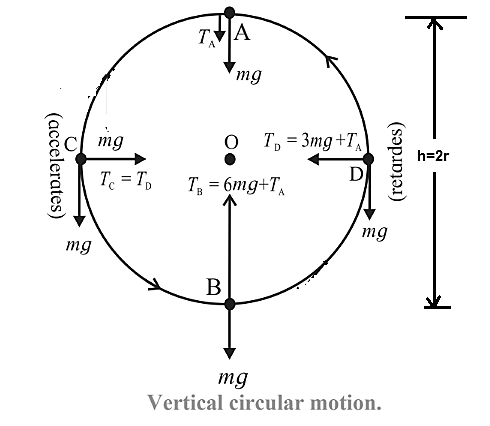
At the top position (Point A) : Let va be the speed of the particle and TA the tension in the string. Here both, weight mg and force due to tension TA are downwards, i.e. towards the centre. In this case, net force on the particle towards the center O is TA + mg is their resultant as the centripetal force.
∴ TA +mg = \frac{m{v_A}^2}{r} ……..(1)
For minimum possible speed at this point (or if the motion is to be realized with minimum possible energy),
TA = 0
∴ 0 + mg = \frac{m{v_A}^2}{r}
∴ \frac{m{v_A}^2}{r} = mg
That is the particle’s weight alone is the necessary centripetal force at the point A.
∴ vA2 = rg
∴ vA = \sqrt{rg} ……..(2)
At the bottom position (Point B): Let vB The speed at bottom. Taking reference level for zero potential energy to the bottom of the circle, the particle has only kinetic energy \frac{1}{2}m{v_B}^2 at the lowest point.
Total energy at the bottom = KE + PE
= \frac{1}{2}m{v_B}^2+ 0 = \frac{1}{2}m{v_B}^2 …… (3)
As the particle goes from the bottom to the top of the circle, it rises through a height h=2r Therefore potential energy at top is
mgh=mg(2r) and from eq. 2 its minimum KE there is
\frac{1}{2}m{v_A}^2= \frac{1}{2}mgr …… (4)
Minimum Total energy at the top = KE+PE
= \frac{1}{2}mgr + 2mgr= \frac{5}{2}mgr…… (5)
Assuming that the total energy of the particle is conserved,
Total energy at the bottom = Total energy at the top.
From eq. 4 & 5
\frac{1}{2}m{v_B}^2 = \frac{5}{2}mgr
The minimum speed the particle must have at the bottom is
vB =\sqrt{5gr} …….. (6)
(iii) At the midway (Point C)
Let vC be the speed at point C, so that the kinetic energy is \frac{1}{2}m{v_C}^2
At C the particle is at height r from the bottom of the circle.
Therefor PE at C is mgr
Total Energy at C
= \frac{1}{2}m{v_C}^2 + mgr……. (7)
From the law of conservation of energy total energy at C = total energy at B
∴ \frac{1}{2}m{v_C}^2 + mgr = \frac{5}{2}mgr
∴ vC2 = 5gr-2gr = 3gr
∴ vC = \sqrt{3gr}
b. Is zero speed possible at the uppermost point? Under what conditions? (1 mark)
In a nonuniform vertical circular motion, e.g., those of a small body attached to a string or the loop maneuvers of an aircraft or motorcycle or skateboard, the body must have some minimum speed to reach the top and complete the circle. In this case, the motion is controlled only by gravity and zero speed at the top is not possible.
However, in a controlled vertical circular motion, e.g., those of a small body attached to a rod or the giant wheel (Ferris wheel) ride, the body or the passenger seat can have zero speed at the top, i.e., the motion can be brought to a stop.
c. Also prove that the difference between the extreme tensions (or normal forces) depends only upon the weight of the object. (3 marks)
Consider a small body (or particle) of mass m tied to a string and revolved in a vertical circle of radius rat a place where the acceleration due to gravity is g. At every instant of its motion, the body is acted upon by two forces, namely, its weight mg and the tension T in the string.
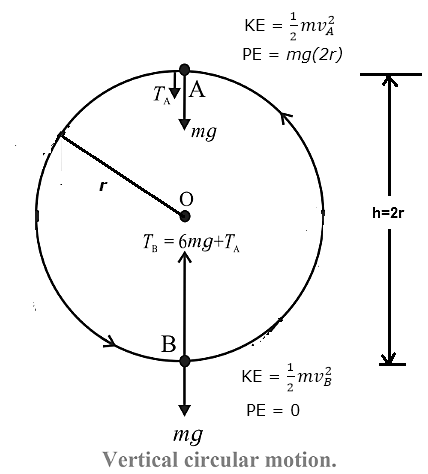
Let vB be the speed of the body and TB be the tension in the string at the lowest point B. We take the reference level for zero potential energy to be the bottom of the circle. Then, the body has only kinetic energy at the lowest point.
TB = \frac{m{v_B}^2}{r}+mg .........(1)
Total energy at the bottom is KE+PE
= \frac{1}{2}m{v_B}^2+0
= \frac{1}{2}m{v_B}^2 ..........(2)
Let vA be the speed of the body and TA be the tension in the string at the lowest point A. As the body goes from B to A it rises through a height h=2r
∴ TA = \frac{m{v_A}^2}{r}-mg .........(3)
Total energy at A = KE+PE
= \frac{m{v_A}^2}{r}+mg(2r) .........(4)
Then from eq. (1) and (3)
TB - TA = \frac{m{v_B}^2}{r}+mg- \frac{m{v_A}^2}{r}-mg
∴ TB - TA = \frac{m}{r}({v_B}^2-{v_A}^2) +2mg .........(5)
Assuming that the total energy of the body is conserved,
Total energy at the Bottom=Total energy at Top
From eq. (2) and (4)
\frac{1}{2}m{v_B}^2= \frac{m{v_A}^2}{r}+mg(2r)
vB2-vA2 = 4gr .........(6)
Substituting this in eq. (5)
TB - TA = \frac{m}{r}(4gr) +2mg
∴ TB - TA = 4mg+2mg = 6mg
Therefore difference in the tensions in the string at the highest and the lowest point is 6 times the weight of the body.
Question 5
a. Discuss the necessity of radius of gyration. Define it. On what factors does it depend and it does not depend? (2 marks)
Definition: The radius of gyration of a body rotating about an axis is defined as the distance between the axis of rotation and the point at which the entire mass of the body can be supposed to be concentrated so as to give the same moment of inertia as that of the body about the given axis.
The moment of inertia (MI) of a body about a given rotation axis depends upon
(i) the mass of the body and
(ii) the distribution of mass about the axis of rotation.
These two factors can be separated by expressing the MI as the product of the mass (M) and the square of a particular distance (k) from the axis of rotation. This distance is called the radius of gyration and is defined as given above.
Thus,
I= \sum \limits_{i} m_ir^2_i
∴ k= \sqrt\frac{I}{M}
Physical significance : The radius of gyration is less if I is less, i.e., if the mass is distributed close to the axis; and it is more if I is more, i.e., if the mass is distributed away from the axis. Thus, it gives the idea about the distribution of mass about the axis of rotation.
b. Can you locate some similarity between the centre of mass and radius of gyration? (2 marks)
The centre of mass (CM) coordinates locates a point where if the entire mass M of a system of particles or that of a rigid body can be thought to be concentrated such that the acceleration of this point mass obeys Newton’s second law of motion, viz.
F = MaCM, where F is the sum of all the external forces acting on the body or on the individual particles of the system of particles.
Similarly, radius of gyration locates a point from the axis of rotation where the entire mass M can be thought to be concentrated such that the angular acceleration of that point mass about the axis rotation obeys the relation, τ = Mα , where τ is the sum of all the external torques acting on the body or on the individual particles of the system particles.
c. What can you infer if a uniform ring and a uniform disc have the same radius of gyration? (2 marks)
Consider a uniform ring and a uniform disc, both of the same mass M and same radius R.
Let Ir and Id be their respective moment of inertias.
If Kr and Kd are their respective radii of gyration, we can write,
Ir = MR2 = MKr2
∴Kr = R and
Id = (1/2) MR2 = MKd2
∴ Kd = R/ \sqrt{2}
∴ Kd < Kr
It shows mathematically that K is decided by the distribution of mass.
In a ring the entire mass is distributed at the distance R,
While for a disc, its mass is distributed between 0 and R.
Among any objects of same mass and radius, ring has the largest radius of gyration and hence maximum M.I.
Question 6
State the conditions under which the theorems of parallel axes and perpendicular axes are applicable. State the respective mathematical expressions.
The theorem of parallel axis is applicable to any body of arbitrary shape. The moment of inertia (MI) of the body about an axis through the centre mass should be known, say, ICM. Then, the theorem can be used to find the MI, I, of the body about an axis parallel to the above axis. If the distance between the two axes is h,
I= ICM + Mh2
The theorem of perpendicular axes is applicable to a plane lamina only. The moment of inertia of a plane lamina about an axis—the z axis-perpendicular to its plane is equal to the sum of its moments of inertia Ix and Iy about two mutually perpendicular axes x and y in its plane and through the point of intersection of the perpendicular axis and the lamina.
Iz=Ix+Iy
Question 7
Derive an expression that relates angular momentum with the angular velocity of a rigid body.
Consider a rigid body rotating with a constant angular velocity w about an axis through the point O and perpendicular to the plane of the figure. All the particles of the body perform uniform circular motion about the axis of rotation with the same angular velocity ω
Suppose that the body consists of N particles of masses m1, m2, ..., mn, situated at perpendicular distances r1, r2, ..., rn, respectively from the axis of rotation.
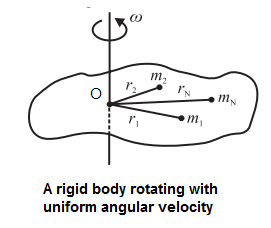
The particle of mass m, revolves along a circle of radius r,, with a linear velocity of magnitude
v1= r1ω The magnitude of the linear momentum of the particle is
p1 = m1v1 = m1r1ω
The angular momentum of the particle about the axis of rotation is by definition,
\vec{L_1}=\vec{r_1}\vec{p_1}
\ L1 = r1 p1sinq
where θ is the smaller of the two angles between r1 and p1
In this case, θ = 90° ∴ sinθ = 1
∴ L1 = r1 p1 = r1m1r1ω = m1r12ω
Similarly, L2 = m2r22ω, L3 = m3r32ω etc.
The angular momentum of the body about the given axis is
L= L1 + L2 +L3 ……. + LN
= m1r12ω + m2r22ω + m3r32ω …….. mNrN2ω
= ω (m1r12 + m2r22 + m3r32 …….. mNrN2)
= (\sum \limits_{i=1}^{N}m_ir_i^2)ω
∴ L=I ω
where I = (\sum \limits_{i=1}^{N}m_ir_i^2)
= moment of inertia of the body about the given axis.
In vector form, \vec{L}=I\vec{ω}
Thus, angular momentum = moment of inertia x angular velocity.
Note: Angular momentum is a vector quantity. It has the same direction as \vec{ω}
Question 8
Obtain an expression relating the torque with angular acceleration for a rigid body.
A torque acting on a body produces angular acceleration.
Figure shows a rigid object rotating with a constant angular acceleration a about an axis perpendicular to the plane of paper.
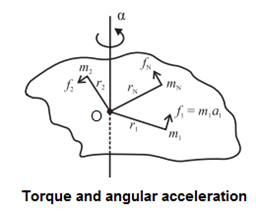
For theoretical simplification let us consider the object to be consisting of N number of particles of masses m1, m2 , ..... mN
at respective perpendicular distances r1, r2,.....rN from the axis of rotation.
As the object rotates, all these particles perform circular motion with same angular acceleration a, but with different linear (tangential) accelerations
a1=r1α, a2=r2α, a3=r3α, …….., aN=rNα, etc.
Force experienced by the first particle is
f1=m1a1= m1r1α,
As these forces are tangential, their respective perpendicular distances from the axis are r1, r2,.....rN
Thus, the torque experienced by the first particle is of magnitude τ1 =f1r1 = m1r12α
Similarly, τ2 = m2r22α, τ3 =f3r3 = m3r32α …….., τN =fNr3 = mNrN2α
If the rotation is restricted to a single plane, directions of all these torques are the same, and along the axis. Magnitude of the resultant torque is then given by
τ = τ1 + τ2 +τ3 …………, +τN
= α (m1r12 + m2r22 + m3r32 …….. mNrN2) = Iα
where, I = m1r12 + m2r22 + m3r32 …….. mNrN2 is the moment of inertia of the object about the given axis of rotation.
This gives the required relation τ = Iα
Angular acceleration vec{α} has the same direction as torque \vec{t} and both them are axial vectors.
Question 9
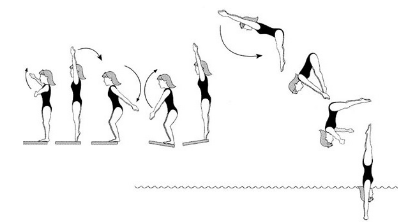
State and explain the principle of conservation of angular momentum. Use a suitable illustration. Do we use it in our daily life? When?
Law (or principle) of conservation of angular momentum : The angular momentum of a body is conserved if the resultant external torque on the body is zero.
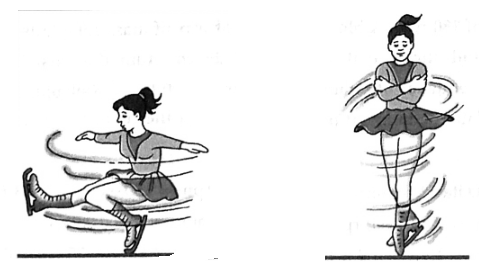
Explanation : This law (or principle) is used by a figure skater or a ballerina to increase their speed of rotation for a spin by reducing the body’s moment of inertia. A diver too uses it during a somersault for the same reason.
(1) Ballet dancers: During ice ballet, the dancers have to undertake rounds of smaller and larger radii. The dancers come together while taking the rounds of smaller radius (near the centre). In this case, the moment of inertia of their system becomes minimum and the frequency increases, to make it thrilling. While outer rounds, the dancers outstretch their legs and arms. This increases their moment of inertia that reduces the angular speed and hence the linear speed. This is essential to prevent slipping.
(2) Diving : Take-off from a springboard or diving platform determines the diver’s trajectory and the magnitude of angular momentum. A diver must generate angular momentum at take-off by moving the position of the arms and by a slight hollowing of the back. This allows the diver to change angular speeds for twists and somersaults in flight by controlling her/his moment of inertia. A compact tucked shape of the body lowers the moment of inertia for rotation of smaller radius and increased angular speed. The opening of the body for the vertical entry into water does not stop the rotation, but merely slows it down. The angular momentum remains constant throughout the flight.
Question 10
Discuss the interlink between translational, rotational and total kinetic energies of a rigid object that rolls without slipping. (1 mark)
The objects like a cylinder, sphere, wheels, etc. are quite often seen to perform rolling motion. In the case of pure rolling, two motions are undertaking simultaneously; circular motion and linear motion.
Individual motion of the particles (except the one at the centre of mass) is too difficult to describe. However, for theory considerations we can consider the actual motion to be the result of
(i) circular motion of the body as a whole, about its own symmetric axis and
(ii) linear motion of the body assuming it to be concentrated at its centre of mass. In other words, the centre of mass performs purely translational motion.
Accordingly, the object possesses two types of kinetic energies, rotational and translational. Sum of these two is its total kinetic energy.
E = Etran + Erot ... (1)
where Etran and Erot are the kinetic energies associated with translation of the center of mass CM and rotation about an axis through the CM, respectively.
Let M and R be the mass and radius of the body.
Let ω, k and I be the angular speed, radius of gyration and moment of inertia for rotation about an axis through its centre, and v be the translational speed of the centre of mass.
v = ωR and I = MK2
Etran = \frac{1}{2}mv^2 and Erot = \frac{1}{2}Iω^2
Total kinetic energy of rolling = Translational K.E. + Rotational K.E.
∴ E = \frac{1}{2}Mv^2 + \frac{1}{2}Iω^2
= \frac{1}{2}Mv^2 + \frac{1}{2}I\frac{v^2}{r^2}
= \frac{1}{2}Mv^2(1+ \frac{I}{Mr^2})
= \frac{1}{2}Mv^2(1+ \frac{MK^2}{Mr^2})
= \frac{1}{2}Mv^2(1+ \frac{K^2}{r^2})
Question 11
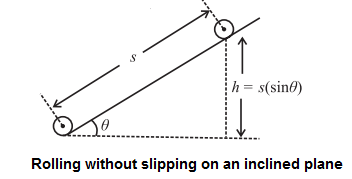
A rigid object is rolling down an inclined plane. Derive expressions for the acceleration along the track and the speed after falling through a certain vertical distance.
Consider a symmetric rigid body, like a sphere or a wheel or a disc, rolling on a plane surface with friction down a plane inclined at an angle q to the horizontal. If the frictional force on the body is large enough, the body rolls without slipping.
Let M and R be the mass and radius of the body.
Let I be the moment of inertia of the body for rotation about an axis through its centre. Let the body start from rest at the top of the incline at a height ft. Let v be the translational speed of the centre of mass at the bottom of the incline. Then, its kinetic energy at the bottom of the incline is
E = \frac{1}{2}Mv^2(1+ \frac{I}{Mr^2}
= \frac{1}{2}Mv^2(1+ β)\) .... (....β=\frac{I}{MR^2})
If K is the radius of gyration of the body,
I= MK2 and β=\frac{1}{MR^2} = \frac{K^2}{R^2}
From conservation of energy,
(KE + PE)initial = (KE + PE)final
∴ 0 + Mgh =\frac{1}{2}Mv^2(1+ β)\)+ 0
∴ Mgh =\frac{1}{2}Mv^2(1+ β)\)
v^2=\frac{2gh}{1+β}
v=\sqrt{\frac{2gh}{1+β}}
v=\sqrt{\frac{2gh}{1+\frac{k^2}{R^2}}}
Since h=Lsinθ
v=\sqrt{\frac{2gLsinθ}{1+\frac{k^2}{R^2}}}
Let a be the acceleration of the centre of mass of the body along the inclined plane. Since the body starts from rest,
v2 = 2aL ∴ a= v2/2L
a = \frac{2gLsinθ}{1+\frac{k^2}{R^2}}.\frac{1}{2L}
= \frac{gsinθ}{1+\frac{k^2}{R^2}} = \frac{gsinθ}{1+β}
Starting from rest, if tis the time taken to travel the distance L,
L= (½)at2
∴ t2 =\sqrt{\frac{2L}{a}} = \sqrt{\frac{2L}{gsinθ}(1+\frac{K^2}{R^2}}
Question 12
Somehow, an ant is stuck to the rim of a bicycle wheel of diameter 1 m. While the bicycle is on a central stand, the wheel is set into rotation and it attains the frequency of 2 rev/s in 10 seconds, with uniform angular acceleration. Calculate
(i) Number of revolutions completed by the ant in these 10 seconds. (2marks)
(ii) Time taken by it for first complete revolution and the last complete revolution. (3marks)
Given- r=0.5 m, ω0 = 0, ω = 2 rev/s t = 10 s
(i) Angular acceleration α is constant,
Average angular speed ωav = \frac{ω_0 +ω}{2} = \frac{0+2}{2} = 1 rev/s
∴ Angular displacement of the wheel in time t,
θ = ωav,×t = 1 × 10 = 10 revolutions
Answer is 10 revolutions
(ii) α = \frac{ω-ω_0}{t} = \frac{2-0}{10}=\frac{1}{5} rev/s2
θ = ω0,×t + \frac{1}{2} αt^2 = 0 + \frac{1}{2} αt^2 (...ω0 = 0)
∴ for θ1 = 1 rev
1= \frac{1}{2}×\frac{1}{5}t{_1}^2
t12 =10
t1 = \sqrt{10}s = 3.162 s
Time for first revolution = 3.162 s
for θ2 = 9 rev
9= \frac{1}{2}×\frac{1}{5}t{_2}^2
t22 =90
∴ t2 = \sqrt{90} s = 9.486 s
∴Time for last i.e 10 th revolution is
t - t2 = 10- 9.486 = 0.514 s
∴Time for first revolution = 0.514 s
Question 13.
Coefficient of static friction between a coin and a gramophone disc is 0.5. Radius of the disc is 8 cm. Initially the centre of the coin is π cm away from the centre of the disc. At what minimum frequency will it start slipping from there? By what factor will the answer change if the coin is almost at the rim?
(use g = π2 m/s2 ) (3marks)
Given: ms=0.5, r1 = π cm = π x10-2 m, r2 = 8 cm = 8x 10-2 m, g=π2 m/s2
To revolve with the disc without slipping, the necessary centripetal force must be less than or equal to the limiting force of static friction.
∴ mω2r ≤ μs mg
∴ ω2r ≤ μs g
4π2f2min r = μs g …(1) (…ω=2πf)
∴ for r = r1
4π2f2min-1 r1= μs g
f2min1= \frac{μ_sg}{4π^2r_1} = \frac{0.5π^2}{4π^2(π×10^{-2})}
f2min1= \frac{100}{8π}=\frac{25}{2π}
∴ fmin1 = \frac{5}{\sqrt{2π}}
At frequency \frac{5}{\sqrt{2π}} rps, the coin will start slipping
From Eq. 1
f2min α \frac{1}{r}
∴ \frac{f_{min2}}{f_{min1}} =\sqrt{\frac{r_2}{r_1}} = \sqrt{\frac{π}{8}}
∴f_{min2} = \sqrt{\frac{π}{8}} f_{min1}
In the second case minimum frequency will be \sqrt{\frac{π}{8}} times that in the first case
(in text book answer is given for r1=2cm)
Question 14.
Part of a racing track is to be designed for a curvature of 72 m. We are not recommending the vehicles to drive faster than 216 kmph. With what angle should the road be tilted? By what height will its outer edge be, with respect to the inner edge if the track is 10 m wide?
Given : r=72m, v0 =216 kmph = 216 ×1000/3600 m/s = 60m/s
w= 10m, g= 10m/s2
tanθ = \frac{v^2_0}{rg} =\frac{60^2}{72×10}
∴ θ= tan-15 = 78°4’
78°4’ is the required angle of banking.
sinθ=h/w
∴ h =w sinθ = 10 ´ sin78°4’ = 10 ´ 0.9805
∴ h = 9.8 m
9.8 m is the height of the outer edge of the rack relative to the inner edge.
Question 15.
The road in the question 14 above is constructed as per the requirements. The coefficient of static friction between the tyres of a vehicle on this road is 0.8, will there be any lower speed limit? By how much can the upper speed limit exceed in this case?
r=72m, θ= 78°4’(from above question) , us=0.8, g= 10m/s2 , tanθ= tan78°4’ =5
vmin = \sqrt{rg(\frac{tanθ-u_s}{1+u_stanθ})}
= \sqrt{72×10(\frac{5-0.8}{1+(0.8×5)})}
vmin = 24.588 m/s = 88.52 km/h
88.52 km/h will be the lower limit or minimum speed on this track.
Since the track is heavily banked q>45° there is no upper limit or maximum speed on this track.
Question 16.
During a stunt, a cyclist (considered to be a particle) is undertaking horizontal circles inside a cylindrical well of radius 6.05 m. If the necessary friction coefficient is 0.5, how much minimum speed should the stunt artist maintain?
Mass of the artist is 50 kg. If she/he increases the speed by 20%, how much will the force of friction be? (3marks)
Given : r=6.05m, μs = 0.5, g=10m/s2 , m=50kg, ∆v=20%
vmin = \sqrt{\frac{rg}{μ_s}}
∴ vmin = \sqrt{\frac{6.05×10}{0.5}} = \sqrt{121} =11 m/s
11m/s is the required minimum speed
So long as the cyclist is not sliding, at every instant, the force of static friction is
fs=mg = 50×10 = 500 N
Question 14.
Part of a racing track is to be designed for a curvature of 72 m. We are not recommending the vehicles to drive faster than 216 kmph. With what angle should the road be tilted? By what height will its outer edge be, with respect to the inner edge if the track is 10 m wide? (3marks)
Given : r=72m, v0 =216 kmph = 216 ×1000/3600 m/s = 60m/s
w= 10m, g= 10m/s2
tanθ =\frac{{v_0}^2}{rg} =\frac{60^2}{72×10} = 5
∴θ= tan-15 = 78°4’
78°4’ is the required angle of banking.
sinθ=h/w
∴ h =w sinθ = 10 × sin78°4’ = 10 × 0.9805
∴ h = 9.8 m
9.8 m is the height of the outer edge of the rack relative to the inner edge.
Question 15.
The road in the question-14 above is constructed as per the requirements. The coefficient of static friction between the tyres of a vehicle on this road is 0.8, will there be any lower speed limit? By how much can the upper speed limit exceed in this case?
Given : r=72m, θ= 78°4’ , μs=0.8, g= 10m/s2 , tanθ= tan78°4’ =5
vmin = \sqrt{rg(\frac{tanθ-μ_s}{1+μ_stanθ})}
vmin = \sqrt{72×10(\frac{5-0.8}{1+(0.8((5)})}
vmin = 24.588 m/s = 88.52 km/h
88.52 km/h will be the lower limit or minimum speed on this track.
Since the track is heavily banked θ > 45° there is no upper limit or maximum speed on this track.
Question 16.
During a stunt, a cyclist (considered to be a particle) is undertaking horizontal circles inside a cylindrical well of radius 6.05 m. If the necessary friction coefficient is 0.5, how much minimum speed should the stunt artist maintain?
Mass of the artist is 50 kg. If she/he increases the speed by 20%, how much will the force of friction be? (3marks)
Given : r = 6.05 m, μs = 0.5, g = 10 m/s2 , m = 50kg, ∆v = 20%
vmin = \sqrt{\frac{rg}{μ_s}}
= \sqrt{\frac{6.05×10}{0.5}}
= \sqrt{12.1×10} =\sqrt{121} = 11 m/s
∴ 11 m/s is the required minimum speed
So long as the cyclist is not sliding, at every instant, the force of static friction is
fs= mg = 50 × 10 = 500 N
Question 17.
A pendulum consisting of a massless string of length 20 cm and a tiny bob of mass 100 g is set up as a conical pendulum. Its bob now performs 75 rpm.
Calculate kinetic energy and increase in the gravitational potential energy of the bob. (Use π2 = 10 ) (4mark)
Given : L= 0.2 m, m = 0.1 kg, n = 75 rpm = 75/60 = 5/4 rps, g = 10 m/s2 , π2 = 10
T=1/n =4/5 s = 0.8 s
T = 2π\sqrt{\frac{L\,\,cosθ}{g}}
T2 = 4π2 \frac{L\,\,cosθ}{g}
h= L cosθ = \frac{gT^2}{4π^2}
= \frac{10×0.8^2}{4×10} =0.16 m ……(1)
∴ cosθ = 0.16/0.2 =0.8
∴ θ = cos-1 0.8 =36.87° = 36°5’
v2 = rg tanθ = (L sin36.87°)(g)(tan36.87°) .(....r = Lsinθ)
=(0.2 × 0.6)(10)(0.75) = 0.9
The KE of the bob = \frac{1}{2}mv^2 = \frac{1}{2}(0.1 × 0.9) = 0.045 J
The increase in gravitational PE
∆PE= mg(L− h) =(0.1)(10)(0.2 − 0.16) = 0.04 J
Question 18.
A motorcyclist (as a particle) is undergoing vertical circles inside a sphere of death. The speed of the motorcycle varies between 6 m/s and 10 m/s. Calculate diameter of the sphere of death. How much minimum values are possible for these two speeds?
Given : Speed at Top vt =6 m/s, Speed at Bottom = vb =10m/s, g=10 m/s2
vb2= vt2 + 4gr
∴ r= (vb2 - vt2)/4g = (102 -62)/(4´10) = 64/40
∴ r = 1.6m
∴ The diameter of the sphere of death = 3.2m
For this r minimum speed at top
vmin =\sqrt{gr} at the top
∴ vmin =\sqrt{10×1.6} =\sqrt{16}=4 m/s
Corresponding minimum speed at bottom= \sqrt{5gr}=4\sqrt{5}m/s
The required minimum values of the speed are 4 m/s and 4\sqrt{5}m/s m/s
Question 19.
A metallic ring of mass 1 kg has moment of inertia 1 kg m2 when rotating about one of its diameters. It is molten and remoulded into a thin uniform disc of the same radius. How much will its moment of inertia be, when rotated about its own axis. (2 marks)
The MI of the thin ring about its diameter,
Ir = \frac{1}{2}MR2 = 1 kg-m2
Since the ring is melted and recast into a thin disc of same radius R, the mass of the disc equals the mass of the ring = M.
The MI of the thin disc about its own axis (i.e. transverse symmetry axis) is
Id= \frac{1}{2}MR2 = Ir
∴ Id = 1 kg-m2
Question 20.
A big dumb-bell is prepared by using a uniform rod of mass 60 g and length 20 cm. Two identical solid spheres of mass 50 g and radius 10 cm each are at the two ends of the rod. Calculate moment of inertia of the dumb-bell when rotated about an axis passing through its centre and perpendicular to the length. (2 marks)
Given : Mass of sphere Ms=50g, Radius of sphere Rs = 10 cm, Mass of rod Mr = 60g, Length of rod Lr = 20 cm
The MI of a solid sphere about its diameter is
Is-CM = \frac{2}{5} MsRs2
The distance of the rotation axis (transverse symmetry axis of the dumbbell) from the centre of sphere,
h =30 cm.
The MI of a solid sphere about the rotation axis,
Is = Is-CM + Ms h2
For the rod, the rotation axis is its transverse symmetry axis through CM.
The MI of a rod about this axis,
Ir =\frac{1}{12} MrLr2
Since there are two solid spheres, the MI of the dumbbell about the rotation axis is
I= 2Is + Ir
= 2Ms ( \frac{2}{5}Rs2 + h2) + \frac{1}{12}MrLr2
= 2(50) ( \frac{2}{5}(10)2 + (30)2 ) + \frac{1}{12}(60)(20)2
= 100 (40 + 900) + 5(400) = 94000 + 2000
= 96000 g-cm2
Question 21.
A flywheel used to prepare earthenware pots is set into rotation at 100 rpm. It is in the form of a disc of mass 10 kg and radius 0.4 m. A lump of clay (to be taken equivalent to a particle) of mass 1.6 kg falls on it and adheres to it at a certain distance x from the centre. Calculate x if the wheel now rotates at 80 rpm.
Given : f1 = 100 rpm, f2= 80 rpm, M =10 kg, R = 0.4m, m = 1.6kg
I1=Iwheel = \frac{1}{2}MR^2= (1/2)(10)(0.4)2 = 0.8 kg-m2
MI of the wheel and lump of the clay is
I2 = Iwheel + mx2
By the principle of conservation of angular momentum
I1w1 = I2w2
I1(2πf1) = I2(2πf2)
I2 = Iwheel + mx2 = \frac{f_1}{f_2}I_1 = \frac{f_1}{f_2}I_{wheel}
∴ mx2 = (\frac{f_1}{f_2}-1)I_{wheel}
∴ mx2= (\frac{100}{80}-1)(0.8)= 0.2 kg-m2
∴ x2 = 0.2/1.6= 1/8
∴ x= = 0.3536 m
Question 22.
Starting from rest, an object rolls down along an incline that rises by 3 in every 5 (along it). The object gains a speed of m/s as it travels a distance of 5/3 m along the incline. What can be the possible shape/s of the object?
Given : sinq=3/5, u=0, v = \sqrt{10} m/s L=5/3 m, g= 10 m/s2
v=\sqrt{\frac{2gLsinθ}{1+\frac{k^2}{R^2}}}
= \sqrt{\frac{2gLsinθ}{1+β}}
∴ v^2=\frac{2gLsinθ}{1+β}
∴ 1+β =\frac{2gLsinθ}{v^2} = \frac{2×10×(5/2)(2/5}{(\sqrt{10})^2} = 2
∴ β = 1 = k2/R2
Therefore the body rolling down is either cylindrical shell or ring
Useful links :
| Main Page : - Maharashtra Board Class 12-Physics - All chapters notes, solutions, videos, test, pdf.
Next Chapter :Chapter-2-Mechanical Properties of Fluids - Online Solution |
Thank you