Mechanical Properties of Fluid
Class-12th-Physics-Chapter-2-Maharashtra Board
Solution
Question 1.
1) Multiple Choice Questions
i) A hydraulic lift is designed to lift heavy objects of maximum mass 2000 kg. The area of cross section of piston carrying the load is 2.25 × 10-2 m2. What is the maximum pressure the smaller piston would have to bear?
(A) 0.8711 × 106 N/m2
(B) 0.5862 × 107 N/m2
(C) 0.4869 × 105 N/m2
(D) 0.3271 × 104 N/m2
(A) 0.8711 × 106 N/m2
ii) Two capillary tubes of radii 0.3 cm and 0.6 cm are dipped in the same liquid. The ratio of heights through which the liquid will rise in the tubes is
(A) 1:2 (B) 2:1 (C) 1:4 (D) 4:1
(B) 2:1
iii) The energy stored in a soap bubble of diameter 6 cm and T = 0.04 N/m is nearly
(A) 0.9 × 10-3 J (B) 0.4 × 10-3 J
(C) 0.7 × 10-3 J (D) 0.5 × 10-3 J
(A) 0.9 × 10-3 J
iv) Two hail stones with radii in the ratio of 1:4 fall from a great height through the atmosphere. Then the ratio of their terminal velocities is
(A) 1:2 (B) 1:12 (C) 1:16 (D) 1:8
(C) 1:16
v) In Bernoulli’s theorem, which of the following is conserved?
(A) linear momentum
(B) angular momentum
(C) mass
(D) energy
(D) energy - is conserved
Question 2.
Answer in brief.
i) Why is the surface tension of paints and lubricating oils kept low? (1 mark)
For better wettability (surface coverage), the surface tension and angle of contact of paints and lubricating oil must be low.
ii) How much amount of work is done in forming a soap bubble of radius r?
Let T be the surface tension of a soap solution. The initial surface area of soap bubble = 0 The final surface area of soap bubble = 2 × 4πr2 ∴ The increase in surface area = 2 × 4πr2 The work done in blowing the soap bubble is W = surface tension x increase in surface area =T × 2 × 4πr2 = 8πr2T
iii) What is the basis of the Bernoulli’s principle? (1 mark)
Conservation of energy is the basis of the Bernoulli’s principle Bernoulli’s equation states that the work done per unit volume of a fluid by the surrounding fluid is equal to the sum of the changes in kinetic and potential energies per unit volume that occur during the flow. In other words, the Bernoulli’s principle is thus consistent with the principle of conservation of energy.
iv) Why is a low density liquid used as a manometric liquid in a physics laboratory? (2 marks)
An open tube manometer measures the gauge pressure, p = p0 + hρg, where p is the pressure being measured, p0 is the atmospheric pressure, h is the difference in height between the manometric liquid of density ρ in the two arms. For a given pressure p, the product hρ is constant. That is, ρ should be small for h to be large. Therefore, for noticeably large h, laboratory manometer uses a low density liquid.
v) What is an incompressible fluid? (1 mark)
A fluid which does not undergo change in volume for a large range of pressures. Thus, its density remains constant throughout the fluid for a large range of pressures. In most cases, all liquids are incompressible.
Question 3.
Why two or more mercury drops form a single drop when brought in contact with each other? (3 marks)
Proof : Let n droplets each of radius coalesce to form a single drop of radius R. As the Volume of the liquid remains constant, volume of the drop = volume of n droplets \(\frac{4}{3}πR^3\) = \(n × \frac{4}{3}πr^3\) ∴ R3=nr3 ∴ R = \(\sqrt[3]{n}\,r\) ....(1) Surface area of n droplets =n × 4πr2 Surface area of the drop = 4πR2 = 4π×n2/3r2 ..... from eq. 1 ∴ Surface area of the drop = n2/3 × 4πr2 ∴ The change in the surface area = surface area of drop — surface area of n droplets = 4πr2 (n2/3 — n) Since the bracketed term is negative, there is a decrease in surface area and a decrease in surface energy. .
Question 4.
Why does velocity increase when water flowing in broader pipe enters a narrow pipe?
When a tube narrows, the same volume occupies a greater length, as schematically shown in Fig. A1 is the cross section of the broader pipe and that of narrower pipe is A2 By the equation of continuity, v2, =(A1/A2)v1 Fig. Speed of fluid increases as it enters a narrower pipe Since A1/A2 > v2 > v1 For the same volume to pass points 1 and 2 in a given time, the speed must be greater at point 2. The process is exactly reversible. If the fluid flows in the opposite direction, its speed decreases when the tube widens.
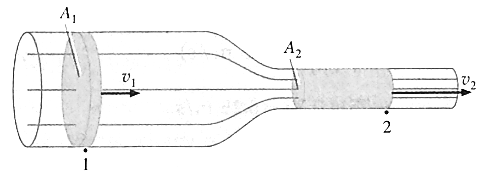
Question 5.
Why does the speed of a liquid increase and its pressure decrease when a liquid passes through constriction in a horizontal pipe?
Consider a horizontal constricted tube. Let A1 and A2 be the cross-sectional areas at points P1 and P2, respectively. Let v1 and v2 be the corresponding flow speeds. ρis the density of the fluid in the pipeline. By the equation of continuity, A1v1 = A2v2 ... (1) v2/ v1 =A1/A2 > 1 (…A1>A2) Therefore, the speed of the liquid increases as it passes through the constriction. Since the meter is assumed to be horizontal, from Bernoulli’s equation we get, \(p_1+\frac{1}{2}ρv_1^2\) = \(p_2+\frac{1}{2}ρv_2^2\) \(p_1+\frac{1}{2}ρv_1^2\) = \(p_2+\frac{1}{2}ρv_1^2(\frac{A_1}{A_2})^2\) ...... from eq.(1) ∴ \(p_1-p_2=\frac{1}{2}ρv_1^2\left[(\frac{A_1}{A_2})^2-1\right]\) Again, since A1>A2 the bracketed term is positive so that p1 > p2. Thus, as the fluid passes through the constriction or throat, the higher speed results in lower pressure at the throat.
Question 6.
Derive an expression of excess pressure inside a liquid drop. (3 marks)
OR
Derive Laplace’s law for a spherical membrane.
Consider a spherical drop as shown in Fig. Let pi be the pressure inside the drop and p0 be the pressure outside it. As the drop is spherical in shape, the pressure, pi, inside the drop is greater than p0, the pressure outside. Therefore, the excess pressure inside the drop is pi - p0. Let the radius of the drop increase from r to r + Δr, where Δr is very small, so that the pressure inside the drop remains almost constant. Let the initial surface area of the drop be A1 = 4πr2, and the final surface area of the drop be A2 = 4π (r+Δr)2 ∴ A2 = 4π (r2 + 2rΔr + Δr2) ∴ A2 = 4π r2 + 8πrΔr + 4πΔr2 As Δr is very small, Δr2 can be neglected, ∴ A2 = 4πr2 + 8πrΔr Thus, increase in the surface area of the drop is dA = A2 – A1 = 4πr2 + 8πrΔr - 4πr2 = 8πrΔr --- (1) Work done in increasing the surface area by dA is stored as excess surface energy. ∴ dW = TdA= T (8πrΔr) --- (2) This work done is also equal to the product of the force F which causes increase in the area of the bubble and the displacement Δr which is the increase in the radius of the bubble. ∴ dW = FΔr --- (3) The excess force is given by, (Excess pressure) × (Surface area) ∴ F = (pi – p0) 4πr2 --- (4) Equating Eq. (2) and Eq. (3), we get, T(8prΔr) = (pi – p0) 4πr2 Δr ∴ (pi – p0) = 2T/r --- (5) This equation gives the excess pressure inside a drop. This is called Laplace’s law of a spherical membrane or Young Laplace Equation in spherical form
Question 7.
Obtain an expression for conservation of mass starting from the equation of continuity. (3 marks)
Consider a fluid in steady or streamline flow, that is its density is constant. The velocity of the fluid within a flow tube, while everywhere parallel to the tube, may change its magnitude. Suppose the velocity is v1 at point P and v2 at point. Q. If A1, and A2, are the cross-sectional areas of the tube at these two points, the volume flux across A1, \(\frac{d}{dt}(V_1)\) = A1v1 and that across A2, \(\frac{d}{dt}(V_2)\) =A2v2 By the equation of continuity of flow for a fluid, A1v1 = A2v2 i.e. \(\frac{d}{dt}(V_1)\) = \(\frac{d}{dt}(V_2)\) If p1 and p2, are the densities of the fluid at P and Q, respectively, the mass flux across A1, \(\frac{d}{dt}(m_1)\) = \(\frac{d}{dt}(p_1v_1)\) = A1p1v1 and that across A2, \(\frac{d}{dt}(m_2)\) = \(\frac{d}{dt}(p_2v_2)\) = A2p2v2 Since no fluid can enter or leave through the boundary of the tube, the conservation of mass requires the mass fluxes to be equal, i.e. \(\frac{d}{dt}(m_1)\) = \(\frac{d}{dt}(m_2)\) A1p1v1 = A2p2v2 i.e. Apv = constant which is the required expression.
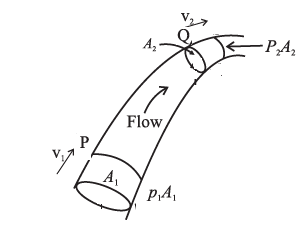
Question 8.
Explain the capillary action. (4 marks)
(1) When a capillary tube is partially immersed a wetting liquid, there is capillary rise and liquid meniscus inside the tube is concave, as shown in Fig. (A). Consider four points A, B, C, D, of which point is just above the concave meniscus inside the capillary and point B is just below it. Points C and D are just above and below the free liquid surface outside. Let PA, PB, PC and PD be the pressures at point A, B, C and D, respectively. Now, PA = PC = atmospheric pressure The pressure is the same on both sides of the free surface of a liquid, so that PC = PD ∴ PA = PD The pressure on the concave side of a meniscus is always greater than that on the convex side, so that PA > PB ∴ PD > PB (….PA = PD) The excess pressure outside presses the liquid up the capillary until the pressures at B and D (at the same horizontal level) equalize, i.e., PB becomes equal to PD. Thus, there is a capillary rise. (2) For a non-wetting liquid, there is capillary depression and the liquid meniscus in the capillary tube is convex, as shown in Fig. (B). Consider again four points A, B, C and D when the meniscus in the capillary tube is at the same level as the free surface of the liquid. Points A and B are just above and below the convex meniscus. Points C and D are just above and below the free liquid surface outside. The pressure at B (PB) is greater than that at A(PA). The pressure at A is the atmospheric pressure H and at D, PD @ H = PA. Hence, the hydrostatic pressure at the same levels at B and D are not equal, PB > PD. Hence, the liquid flows from B to D and the level of the liquid in the capillary falls. This continues till the pressure at B’ is the same as that D’, that is till the pressures at the same level are equal.
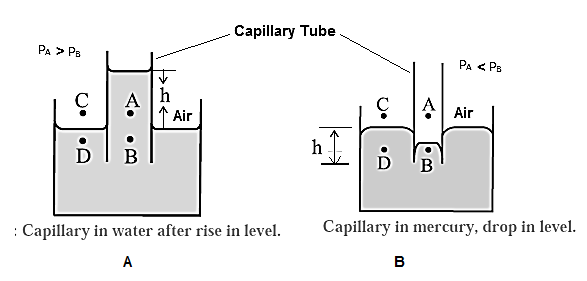
Question 9.
Derive an expression for capillary rise for a liquid having a concave meniscus. (3 marks)
Consider a capillary tube of radius r partially immersed into a wetting liquid of density p. Let the capillary rise be h and q be the angle of contact at the edge of contact of the concave meniscus and glass (Fig).. If R is the radius of curvature of the meniscus then from the figure, r=R cosθ. Surface tension T is the tangential force per unit length acting along the contact line. It is directed into the liquid making an angle θ with the capillary wall. We ignore the small volume of the liquid in the meniscus. The gauge pressure within the liquid at a depth h, i.e. at the level of the free liquid surface open to the atmosphere, is P— Po = ρgh ………. (1) By Laplace’s law for a spherical membrane, this gauge pressure is P— Po = 2T/R …….(2) hρg = 2T/R = \(\frac{2Tcosθ}{r}\) ∴ h = \(\frac{2Tcosθ}{rρg}\)…….(3) Thus, narrower the capillary tube, the greater is the capillary rise. From Eq. (3), T= \(\frac{hrρg}{2Tcosθ}\)………(4) Equations (3) and (4) are also valid for capillary depression h of a non-wetting liquid. In this case, the meniscus is convex and θ is obtuse. Then, cosθ is negative but so is h, indicating a fall or depression of the liquid in the capillary. T is positive in both cases. [For capillary rise, Eq. (3) is also called the ascent formula. ]
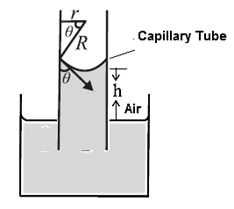
Question 10.
Find the pressure 200 m below the surface of the ocean if pressure on the free surface of liquid is one atmosphere. (Density of sea water = 1060 kg/m3) (2 marks)
Given : h=200 m, ρ=1060 kg/m3 p0 = 1.013×105 Pa, g = 9.8 m/s2 Absolute pressure, P=p0+hρg = (1.013×105 )+(200×1060×9.8) = (1.013×105 )+(20.776×105) = 21.789×105 = 21.789 Mpa
Question 11.
In a hydraulic lift, the input piston had surface area 30 cm2 and the output piston has surface area of 1500 cm2. If a force of 25 N is applied to the input piston, calculate weight on output piston. (2 marks)
Given : A1 = 30 cm2 = 3×10-3 m2 , A2 = 1500 cm2 = 0.15 m2 F1=25 N By Pascal’s law \(\frac{F_1}{A_1}=\frac{F_2}{A_2}\) ∴The force on the output piston, \(F_2=F_1(\frac{A_2}{A_1})\) = (25)\(\frac{0.15}{3×10^3}\) =25 × 50=1250 N Weight on output piston = 1250 N
Question 12.
Calculate the viscous force acting on a rain drop of diameter 1 mm, falling with a uniform velocity 2 m/s through air. The coefficient of viscosity of air is 1.8 × 10-5 Ns/m2. (2 marks)
Given: d= 1 mm, v0 = 2 m/s, h = 1.8 × 10-5 Ns/m2 r =d/2 =0.5 mm = 5 ×10-4 m, By Stoke’s law the viscous force on rain drop is f= 6πηr v0 = 6 ×3.142 x 1.8 × 10-5 x 5 ×10-4 × 2 = 3.394 ×10-7 N
Question 13.
A horizontal force of 1 N is required to move a metal plate of area 10-2 m2 with a velocity of 2 × 10-2 m/s, when it rests on a layer of oil 1.5 × 10-3 m thick. Find the coefficient of viscosity of oil. (3 marks)
Given : F=1, A=10-2 m2, v0 =2 × 10-2 m/s, y=1.5 × 10-3 m Velocity gradient, dv/dy = 2 × 10-2 / 1.5 × 10-3 = 40/3 s-1 Viscous Force, F= \(η\frac{dv}{dy}\) Therefore coefficient of viscosity is η = \(\frac{F}{A(dv/dy)} =\frac{1}{10^{-2}(40/3)}\) = 7.5 Pa-s
Question 14.
With what terminal velocity will an air bubble 0.4 mm in diameter rise in a liquid of viscosity 0.1 Ns/m2 and specific gravity 0.9? Density of air is 1.29 kg/m3.
Given: d=0.4 mm, r=d/2 = 0.2mm= 2×10-4 m, , h = 0.1 Pa-s, pL = 0.9 × 103 kg/m3 = 900 kg/m3, pair = 1.29 kg/m3 g=9.8 m/s2 Since the density of air is less than that of oil, the air bubble will rise up through the liquid. Hence, the viscous force is downward, At terminal velocity, this downward viscous force is equal in magnitude to the net upward force. Viscous force = buoyant force - gravitational force 6πηrvt = \(\frac{4}{3}πr^3(p_L - p_{air})g\) ∴ Terminal velocity, vt = \(\frac{2r^2g(p_{L} - p_{air})}{9η}\) = \(\frac{2×10^{-4}9.8(900 - 1.29)}{9×0.1}\) = 7.829 × 10-4 m/s = 0.7829 mm/s (upwards)
Question 15.
The speed of water is 2m/s through a pipe of internal diameter 10 cm. What should be the internal diameter of nozzle of the pipe if the speed of water at nozzle is 4 m/s2 (2 marks)
Given : d1=10 cm, = 0.1 m, v1 = 2 m/s, v2 = 4 m/s By the equation of continuity, the ratio of the speed is v1/v2 = (d2/d1)2 ∴d2/d1 =\(\sqrt{\frac{v_1}{v_2}}\) =\(\sqrt{\frac{2}{4}}\) =0.707 d2 = 0.707d1 = 0.707(0.1) = 0.0707m
Question 16.
With what velocity does water flow out of an orifice in a tank with gauge pressure 4 × 105 N/m2 before the flow starts? Density of water = 1000 kg/m3. (3 marks)
Given : p-p0 = 4 × 105 N/m2 , ρ = 103 kg/m3 If a orifice at a depth h from the water surface in tank, the gauge pressure there is p-p0 = hρg ….. (1) By Toricellie’s law of reflex, the velocity of efflux v= \(\sqrt{2gh}\)… (2) Substituting for h from eq. 1 v=\(\sqrt{2g(\frac{p-p_0}{ρg})}\) =\(\sqrt{2(\frac{p-p_0}{ρ})}\) =\(\sqrt{2(\frac{4×10^5}{10^3})}\) =\(20\sqrt{2}\) = 28.28 m/s
Question 17.
The pressure of water inside the closed pipe is 3 × 105 N/m2. This pressure reduces to 2 × 105 N/m2 on opening the value of the pipe. Calculate the speed of water flowing through the pipe. (Density of water = 1000 kg/m3). (2 marks)
Given : p1=3 × 105 N/m2 v1=0, p2 = 2 × 105 N/m2 , ρ = 1000 kg/m3 Assuming potential head to be zero, i.e. the pipe to be horizontal, the Bernoulli equation is p1 +(1/2) ρv12 = p2 +(1/2) ρv22 ∴ v22 = \(\frac{2(p_1-p_2)}{ρ}\) …..(..v1=0) ∴ v22 = \(\frac{2(3-2)10^5}{10^3}\) v22=200 v2 = \(10\sqrt{2}\) =14.14 m/s
Question 18.
Calculate the rise of water inside a clean glass capillary tube of radius 0.1 mm, when immersed in water of surface tension 7 × 10-2 N/m. The angle of contact between water and glass is zero, density of water = 1000 kg/m3, g = 9.8 m/s2. (2 marks)
Given : r=0.1 mm = 1 x 10-4 m, θ =0°, T= 7 × 10-2 N/m, p=103 kg/m3, g = 9.8 m/s2 , cosθ = cos0 =1 Capillary rise h = \(\frac{2Tcosθ}{rρg}\) = \(\frac{2×7 × 10^{-2}×1}{ 1 × 10^{-4}×1000×9.8}\) = 0.143 m
Question 19.
An air bubble of radius 0.2 mm is situated just below the water surface. Calculate the gauge pressure. Surface tension of water = 7.2 × 10-2 N/m. (1 mark)
Given : r=0.2 mm = 2x10-4 m, T= 7.2 x 10-2 N/m, ρ=103 kg/m3 The gauge pressure inside the bubble = 2T/r = 2(7.2 x 10-2)/(2x10-4) =7.2 x 102 =720 Pa
Question 20.
Twenty seven droplets of water, each of radius 0.1 mm coalesce into a single drop. Find the change in surface energy. Surface tension of water is 0.072 N/m. (3 marks)
Given : r=0.1mm =1 x 10—4 m, T = 0.072 N/m Let R be the radius of the single drop formed due to the coalescence of 27 droplets of mercury. Volume of 27 droplets = volume of the single drop (as the volume of the liquid remains constant.) \(∴27×\frac{4}{3}πr^3 =\frac{4}{3}πR^3\) 27r3=R3 ∴ 3r=R Surface area of 27 droplets = 27 x 4πr2 Surface area of single drop = 4πR2 ∴ Decrease in surface area = 27 x 4πr2 — 4πR2 = 4π (27r2— R2) = 4π [27r2 —(3r)2] = 4π (27r2 —9r2) = 4π x 18r2 ∴The energy released = surface tension x decrease in surface area = T x 4π x 18r2 = 0.472 x 4 x 3.142 x 18 x (1 x 10—4)2 = 1.628 x 10-7 J
Question 21.
A drop of mercury of radius 0.2 cm is broken into 8 droplets of the same size. Find the work done if the surface tension of mercury is 435.5 dyne/cm. (3 marks)
Let R be the radius of the drop and r be the radius of each droplet. Given : R=0.2 cm, n =8, T = 435.5 dyn/cm As the volume of the liquid remains constant, volume of n droplets = volume of the drop \(∴n×\frac{4}{3}πR^3 =\frac{4}{3}πr^3\) \(∴r^3=\frac{R^3}{n}\) \(∴r=\frac{R}{\sqrt[3]{8}}=\frac{R}{2}\) Surface area of the drop = 4πR2 Surface area of n droplets = n x 4πr2. The increase in the surface area = surface area of n droplets—surface area of drop = 4π (nr2— R2) = 4π (8 x R2/4 — R2) = 4π (2 — 1) R2 = 4πR2 ∴The work done = surface tension x increase in surface area = T x 4πR2 = 435.5 x 4 x 3.142 x (0.2)2 = 2.19 x 102 ergs = 2.19 x 10—5 J
Question 22.
How much work is required to form a bubble of 2 cm radius from the soap solution having surface tension 0.07 N/m. (2 marks)
Given: r= 2 cm = 2x10-2 m, T=0.07 N/m Initial surface area of soap bubble = 0 Final surface area of soap bubble =2 ´ 4πr2 \ Increase in surface area = 2 ´ 4πr2 The work done = surface tension x increase in surface area = T x 2 x 4πr2 = 0.07 x 2 x 4 x 3.142 (2 x10-2)2 = 7.038 x 10-4 J
Question 23.
A rectangular wire frame of size 2 cm × 2 cm, is dipped in a soap solution and taken out. A soap film is formed, if the size of the film is changed to 3 cm × 3 cm, calculate the work done in the process. The surface tension of soap film is 3 × 10-2 N/m. (2 marks)
Given : A1 = 2 × 2 cm2 = 4×10-4 m2 , A2 = 3 × 3 cm2 = 9×10-4 m2 T = 3×10-2 N/m2 As the film has two surfaces, the work done is W=2T(A2 – A1) = 2(3×10-2)(9×10-4−4×10-4) = 3.0×10-5 J = 30μJ
Useful links :
| Main Page : - Maharashtra Board Class 12-Physics - All chapters notes, solutions, videos, test, pdf.
Books : MSBSHSE -Class 12th Science Text Books – Chapter wise PDF for download Previous Chapter :Chapter-1-Rotational Dynamics - Online Solution Next Chapter :Chapter-3-Kinetic Theory of Gases and radiation - Online Solution |