Solution
Question 1.
Choose the correct option. M C Q (1 mark each)
i) In an ideal gas, the molecules possess
(A) only kinetic energy
(B) both kinetic energy and potential energy
(C) only potential energy
(D) neither kinetic energy nor potential energy
(A) only kinetic energy
ii) The mean free path λ of molecules is given by
(A) \(\sqrt{\frac{2}{πnd^2}}\)
(B) \(\frac{1}{πnd^2}\)
(C) \(\frac{1}{\sqrt{2}πnd^2}\)
(D) \(\frac{1}{\sqrt{2πnd}}\)
where n is the number of molecules per unit volume and d is the diameter of the molecules.
(C) \(\frac{1}{\sqrt{2}πnd^2}\)
iii) If pressure of an ideal gas is decreased by 10% isothermally, then its volume will
(A) decrease by 9%
(B) increase by 9%
(C) decrease by 10%
(D) increase by 11.11%
(D) increase by 11.11% Use formula P1V1=P2V2, V2/ V1 = 1/0.9=1.1111, (V2- V1)/ V1= (1-1.1111) =0.1111 =11.11%
iv) If a = 0.72 and r = 0.24, then the value of tr is
(A) 0.02 (B) 0.04 (C) 0.4 (D) 0.2
(B) 0.04
v) The ratio of emissive power of perfectly blackbody at 1327° C and 527 °C is
(A) 4:1 (B) 16 : 1 (C) 2 : 1 (D) 8 : 1
(B) 16 : 1
Question 2.
Answer in brief.
i) What will happen to the mean square speed of the molecules of a gas if the temperature of the gas increases? (1 mark)
If the temperature of a gas increases, the mean square speed of the molecules of the gas will increase in the same proportion. V2 = 3nRT/Nm Therefore V2 ∝ T for a fixed mass of gas.
ii) On what factors do the degrees of freedom depend? (1 mark)
The degrees of freedom depends upon
iii) Write ideal gas equation for a mass of 7 g of nitrogen gas. (1 mark)
In the usual notation, PV =nRT. n= Mass of the gas/Molar Mass =7/28= 1/4 Therefore, the corresponding ideal gas equation is PV = \(\frac14\) RT.
iv) If the density of oxygen is 1.44 kg/m3 at a pressure of 105 N/m2, find the root mean square velocity of oxygen molecules. (2 marks)
Given : ρ = 1.44 kg/m3 , P=105 N/m2 ∴ The root mean square velocity of oxygen molecules \(v_{rms} =\sqrt{\frac{3P}{ρ}}\) = \(\sqrt{\frac{3×10^5}{1.44}}\) m/s = 4.564 × 102 m/s
v) Define athermanous substances and diathermanous substances. (1 mark)
Athermanous substances- Substances that don't allow transmission of heat radiation through them are called athermanous substances. i.e. a substance which is largely opaque to thermal radiations. For example, wood, metal, CO2, water vapors, etc. Diathermanous substances – A Substances through which heat radiation can pass are called diathermanous substances. - For example, rock salt, pure air, glass, etc.
Question 3.
When a gas is heated its temperature increases. Explain this phenomenon based on kinetic theory of gases. ( 2 marks)
Question 4.
Explain, on the basis of kinetic theory, how the pressure of gas changes if its volume is reduced at constant temperature. (2 marks)
Question 5.
Mention the conditions under which a real gas obeys ideal gas equation. (1 mark)
A real gas obeys ideal gas equation when temperature is very high and pressure is very low. (**Under these conditions, the density of a gas is very low. Hence, the molecules, on an average, are far away from each other. The intermolecular forces are then not of much consequence.)
Question 6.
State the law of equipartition of energy and hence calculate molar specific heat of mono- and di-atomic gases at constant volume and constant pressure. (4 marks)
Law of equipartition of energy states that for a dynamical system in thermal equilibrium the total energy of the system is shared equally by all the degrees of freedom. The energy associated with each degree of freedom per molecule is \(\frac 12\)kBT, where kB is the Boltzmann's constant. Monatomic gas: For a monatomic gas, each atom has only three degrees of freedom as there can be only translational motion. Hence, the average energy per atom is \(\frac 32\) kBT The total internal energy per mole of the gas is E= \(\frac 32\) NAkBT … where NA is the Avogadro number. Therefore, the molar specific heat of the gas at constant volume is CV =\(\frac{dE}{dT}\) = \(\frac 32\) NAkB = \(\frac 32\) R where R is the universal gas constant. Now, by Mayer’s relation, CP — CV = R, where CP is the specific heat of the gas at constant pressure. CP = CV +R = \(\frac 32\) R +R = \(\frac 52\) R Diatomic gas : Treating the molecules of a diatomic gas as rigid rotators, each molecule has three translational degrees of freedom and two rotational degrees of freedom. Hence, the average energy per molecule is 3(\(\frac 12\) kBT) + 2(\(\frac 12\) kBT)= \(\frac 52\) kBT The total internal energy of mole is \(\frac 52\) NAkBT The molar specific heat at a constant volume CV is For an ideal gas CV (monoatomic gas) = \(\frac{dE}{dT}\) = \(\frac 52\) NAkB = \(\frac 52\) R For an ideal gas CP — CV = R Where CP is the molar specific heat at constant pressure thus CP = R + \(\frac 52\) R = \(\frac 72\) R A soft or non-rigid diatomic molecule has, in addition, one frequency of vibration which contributes two quadratic terms to the energy. Hence, the energy per molecule of a soft diatomic molecule is E = 3(\(\frac 12\) kBT) + 2(\(\frac 12\) kBT) + 2(\(\frac 12\) kBT)= \(\frac 72\) kBT Therefore energy per mole of a soft diatomic module is E = \(\frac 72\) kBT × NA = \(\frac 72\) RT In this case CV = \(\frac{dE}{dT}\) = \(\frac 72\) R and CP = CV + R = \(\frac 72\) R + R = \(\frac 92\) R [Note :for monatomic gas adiabatic constant, γ = CP/CV = \(\frac 53\), for a diatomic gas γ = \(\frac 75\) or \(\frac 97\)]
Question 7.
What is a perfect blackbody ? How can it be realized in practice? (3 marks)
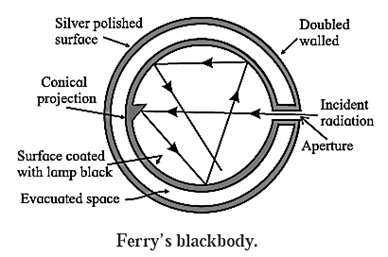
A perfect blackbody or simply a blackbody is defined as a body which absorbs all the radiant energy incident on it. Fery designed a spherical blackbody which consists of a hollow double-walled, metallic sphere provided with a tiny hole or aperture on one side, Fig. The inside wall of the sphere is blackened with lampblack while the outside is silver-plated. The space between the two walls is evacuated to minimize heat loss by conduction and convection. Any radiation entering the sphere through the aperture suffers multiple reflections where about 97 % of it is absorbed at each incidence by the coating of lampblack. The radiation is almost completely absorbed after a number of internal reflections. A conical projection on the inside wall opposite the hole minimizes probability of incident radiation escaping out. When the sphere is placed in a bath of suitable fused salts, so as to maintain it at the desired temperature, the hole serves as a source of blackbody radiation. The intensity and the nature of the radiation depend only on the temperature of the walls. A blackbody, by definition has coefficient of absorption equal to 1. Hence. It’s coefficient of reflection and coefficient of transmission are both zero. The radiation from a blackbody, called blackbody radiation, covers the entire range of the electromagnetic spectrum. Hence, a blackbody is called a full radiator.
Question 8.
State
(i) Stefan-Boltmann law (1 mark)
The Stefan-Boltzmann law : The rate of emission of radiant energy per unit area or the power radiated per unit area of a perfect blackbody is directly proportional to the fourth power of its absolute temperature.
(ii) Wein’s displacement law. (1 mark)
Wien’s displacement law : The wavelength for which the emissive power of a blackbody is maximum, is inversely proportional to the absolute temperature of the blackbody. OR For a blackbody at an absolute temperature T, the product of T and the wavelength λm corresponding to the maximum radiation of energy is a constant. Tλm = b, is constant. (**The value of the constant b in Wien’s displacement law is 2.898 x 10-3 m-K)
Question 9.
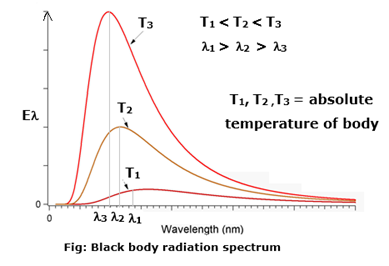
Explain spectral distribution of blackbody radiation. (2 marks)
Blackbody radiation is the electromagnetic radiation emitted by a blackbody by virtue of its temperature. It extends over the whole range of wavelengths of electromagnetic waves. The distribution of energy over this entire range as a function of wavelength or frequency is known as the spectral distribution of blackbody radiation or blackbody radiation spectrum (Fig.). If Eλ is the emissive power of a blackbody in the wavelength range λ and λ+dλ, the energy it emits per unit area per unit time in this wavelength range depends on its absolute temperature T, the wavelength λ and the size of the interval dλ.
Question 10.
State and prove Kirchoff’s law of heat radiation. (3 marks)
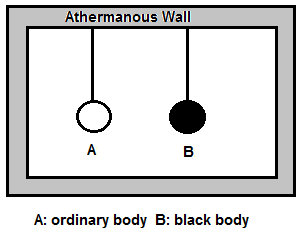
Kirchhoff’s law of heat radiation: At a given temperature, the ratio of the emissive power to the coefficient of absorption of a body is equal to the emissive power of a perfect blackbody at the same temperature for all wavelengths. OR For a body emitting and absorbing thermal radiation in thermal equilibrium, the emissivity is equal to its absorptivity. Proof : Consider an ordinary body A and perfectly black body B of the same dimension suspended in a uniform temperature enclosure as shown in the figure. At thermal equilibrium, both the bodies will have the same temperature as that of the enclosure. Let, E = emissive power of ordinary body A Eb = emissive power of perfectly black body B a = coefficient of absorption of A e = emissivity of A Q = radiant energy incident per unit time per unit area on each body Quantity of heat absorbed per unit area per unit time by body Body A will absorb the quantity aQ per unit time per unit surface area and radiate the quantity R per unit time per unit surface area. Since there is no change in its temperature, we must have, aQ = E .. ....(1) As body B is a perfect blackbody, it will absorb the quantity Q per unit time per unit surface area and radiate the quantity R, per unit time per unit surface area. Since there is no change in its temperature, we must have, Q=Eb ... (2) From Eqs. (1) and (2), we get, a = E/Q = E/Eb …….. (3) From Eq. (3), we get, E/a= Eb But by definition of coefficient of emission e =E/Eb …….. (4) from eq. 3 & 4 we get e=a Hence the proof of kirchoff’s law of radiation
Question 11.
Calculate the ratio of mean square speeds of molecules of a gas at 30 K and 120 K. (2 marks)
Given : T1 = 30K, T2= 120K The mean square speed v2 = \(\frac{3RT}{M_o}\) ∴ \(\frac{v_1^2}{v_2^2} =\frac{T_1}{T_2}\) for given gas ∴ \(\frac{v_1^2}{v_2^2} =\frac{30K}{120K}\) = \(\frac14\) \(\frac14\) is the ratio
Question 12.
Two vessels A and B are filled with same gas where volume, temperature and pressure in vessel A is twice the volume, temperature and pressure in vessel B. Calculate the ratio of number of molecules of gas in vessel A to that in vessel B. (2 marks)
Given : VA = VB , TA=2TB PA=2PB PV=NkBT ∴ No of molecules, N=PV/kBT NA=PAVA/kBTA and NB=PBVB/kBTB ∴ NA/NB = (PA/PB)(VA/VB)(TB/TA) = (2)(2)(1/2)=2 2 is the required ratio.
Question 13.
A gas in a cylinder is at pressure P. If the masses of all the molecules are made one third of their original value and their speeds are doubled, then find the resultant pressure. (2 marks)
Given: m2 = m1/3 v2 = 2v1 Pressure P= \(\frac13 \frac{mN}{v}v^2\) ∴P1= \(\frac13 \frac{m_1N}{v}v_1^2\) ∴P2= \(\frac13 \frac{m_2N}{v}v_2^2\) ∴ \(\frac{P_1}{P_2} =(\frac{m_2}{m_1})(\frac{v_2^2}{v_1^2})\) = \(\frac{\frac{m_1}{3}}{m_1}(2^2)\) = \(\frac43\) P2 = \(\frac43\) P1
Question 14.
Show that rms velocity of an oxygen molecule is 2 times that of a sulfur dioxide molecule at S.T.P. (2 marks)
Given : \(\frac{m_o(SO_2)}{m_o(O_2)}\) = 64/32 =2 The rms speed vrms = \(\sqrt{\frac{3RT}{M_o}}\) vrms ∝ \(\frac{1}{\sqrt{M_o}}\) at constant T \(\frac{v_{rms}(O_2)}{v_{rms}(SO_2)}\) = \(\sqrt{\frac{M_o(SO_2)}{M_o(O_2)}}=\sqrt{2}\) Thus vrms(O2) = \(\sqrt{2}\) vrms(SO2)
Question 15.
At what temperature will oxygen molecules have same rms speed as helium molecules at S.T.P.? (Molecular masses of oxygen and helium are 32 and 4 respectively) (2 marks)
Given : T2 = 273 k, Mo1 (oxygen)= 32 ×10-3 kg/mole, Mo2 (hydrogen)= 4 ×10-3 kg/mole vrms = \(\sqrt{\frac{3RT}{M_o}}\) The rms speed of oxygen molecule v1 = \(\sqrt{\frac{3RT_1}{M_{o1}}}\) The rms speed of helium molecule v2 = \(\sqrt{\frac{3RT_2}{M_{o2}}}\) When v1 = v2 \(\sqrt{\frac{3RT_1}{M_{o1}}}\) = \(\sqrt{\frac{3RT_2}{M_{o2}}}\) ∴ \(\frac{T_1}{M_{o1}}\) = \(\frac{T_2}{M_{o2}}\) ∴ Temprature T1 = \(\frac{M_{o1}}{M_{o2}}.T_2\) = \(\frac{32×10^{-3}×273}{4×10^{-3}}\) = 2184K Answer = 2184 K
Question 16.
Compare the rms speed of hydrogen molecules at 127 ºC with rms speed of oxygen molecules at 27 ºC given that molecular masses of hydrogen and oxygen are 2 and 32 respectively. (2 marks)
Mo1 (hydrogen) = 2 g/mole Mo2 (oxygen) = 32 g/mole T1 (hydrogen) = 273+127=400 K T2 (oxygen) = 273+27=300 K The rms speed vrms = \(\sqrt{\frac{3RT}{M_o}}\) \(\frac{v_{rms1}(hydrogen)}{v_{rms2}(oxygen)}\) = \(\sqrt{\frac{M_{o2}T_1}{M_{o1}T_2}}\) = \(\sqrt{\frac{32×400}{2×300}}\) = \(\frac{8}{\sqrt 3}\)
Question 17.
Find kinetic energy of 5 litre of a gas at S.T.P. given standard pressure is 1.013 × 105 N/m2. (2 marks)
Given : P 1.013 x 105 N/m², V = 5 litres = 5 x 10-3 m E = \(\frac32\) PV = \(\frac32\) (1.013 x 105) (5 x 10-3) = 7.5 x 1.013 x 102 J = 7.597 x 102 J This is the required energy.
Question 18.
Calculate the average molecular kinetic energy (i) per kmol (ii) per kg (iii) per molecule of oxygen at 127 ºC, given that molecular weight of oxygen is 32, R is 8.31 J mol-1 K-1 and Avogadro’s number NA is 6.02 x 1023 molecules mol-1. (3 marks)
Given : T = 273+127 = 400 K, molecular weight=32 \ molar mass = 32 kg/kmol, R = 8.31 Jmol-1 K-1, NA = 6.02 x 1023 molecules mol-1 (i) The average molecular kinetic energy per kmol of oxygen = the average kinetic energy per mol of oxygen x 1000 = \(\frac32\) RT x 1000 = \(\frac32\) (8.31) (400) (10³) = (600)(8.31)(10³) = 4.986 × 106 J/kmol (ii) The average molecular kinetic energy per kg of oxygen = \(\frac{3}{2}\frac{RT}{M_o}\) = \(\frac{4.986×10^6}{32}\) = 1.558 x 105 J/kg. (iii) The average molecular kinetic energy per molecule of oxygen = \(\frac{3}{2}\frac{RT}{N_A}\) = \(\frac{4.986×10^6}{6.02×10^{23}}\) = 8.282 x 10-21 J/molecule
Question 19.
Calculate the energy radiated in one minute by a blackbody of surface area 100 cm2 when it is maintained at 227 ºC. ( Given s= 5.67´10-8 W/m2.K4 ) (2 marks)
Given: t = one minute = 60 s, A = 100 cm2 = 100×10-4 m2 = 10-2 m2, T = 273 + 227 = 500 K, σ= 5.67×10-8 W/m2.K4 The energy radiated, Q = σAT4t = (5.67×10-8)(10-2)(500)4(60) J = (5.67)(625)(60)(10-2)J = 2126 J
Question 20.
Energy is emitted from a hole in an electric furnace at the rate of 20 W, when the temperature of the furnace is 727 ºC. What is the area of the hole? (Take Stefan’s constant σ to be 5.7 ×10-8 J s-1 m-2 K-4) (2 marks)
Given: Q/t = 20W, T=273+727=1000 K, σ = 5.7×10-8 Js-1/m2.K-4 Q/t = σAT4 ∴ The area of the hole, A = (Q/t)/(σT4 ) = 20(5.7×10-8 ×10004 ) = 20×10-4/5.7 m2 = 3.509×10-4 m2
Question 21.
The emissive power of a sphere of area 0.02 m2 is 0.5 kcal s-1 m-2. What is the amount of heat radiated by the spherical surface in 20 second? (1 mark)
Given : R = 0.5 kcal-s-1 'm-2 , A =0.02 m2, t=20s Q = RAt = (0.5) (0.02) (20) = 0.2 kcal 0.2 kcal is the required quantity.
Question 22.
Compare the rates of emission of heat by a blackbody maintained at 727 ºC and at 227ºC, if the blackbodies are surrounded by an enclosure (black) at 27 ºC. What would be the ratio of their rates of loss of heat ? (3 marks)
Given: T1 = 273 + 727 = 1000 K, T2 = 273 + 227 = 500 K, T0 = 273 + 27 = 300 K i) The rate of emission of heat, dQ/dt = σAT4 we assume that the surface area A is the same for the two bodies. \(\frac{(dQ/dt)_1}{(dQ/dt)_2}\) = \(\frac{T_1^4}{T_2^4}\) = \((\frac{T_1}{T_2})^4\) =\((\frac{1000}{500})^4\) = 24 = 16 i) The rate of loss of heat, dQ'/dt = σA( T4 - T04 ) \(\frac{(dQ'/dt)_1}{(dQ/dt)_2}\) = \(\frac{T_1^4-T_0^4}{T_2^4-T_0^4}\) = \(\frac{10^{12}-81×10^8}{625×10^8-81×10^8}\) = 18.23
Question 23.
Earth’s mean temperature can be assumed to be 280 K. How will the curve of blackbody radiation look like for this temperature? Find out λmax. In which part of the electromagnetic spectrum, does this value lie? (2 marks)
Given: T = 280 K, Wien's constant b = 2.897×10-3 m.K λmaxT = b λmax = b /T = 2.897×10-3 / 280 = 1.035 ×10-5 m This value lies in the infrared region of the electromagnetic spectrum. The nature of the curve of blackbody radiation will be the same, but the maximum will occur at 1.035 ×10-5 m
Question 24.
A small-blackened solid copper sphere of radius 2.5 cm is placed in an evacuated chamber. The temperature of the chamber is maintained at 100 ºC. At what rate energy must be supplied to the copper sphere to maintain its temperature at 110 ºC? (Take Stefan’s constant σ to be 5.76 × 10-8 J s-1 m-2 K-4 and treat the sphere as blackbody.) (2 marks)
Given : r = 2.5 cm = 2.5 ×10-2m, T0 = 273+100 = 373 K, T = 273+110 = 383 K, σ = 5.76 × 10-8 J s-1 m-2 K-4 The rate at which energy must be supplied = sA(T4- T04)= σ2πr2 (T4- T04) = (5.76 × 10-8 )(2)(3.142)( 2.5 ×10-2)2( 3834-3734) =0.9624 W
Question 25.
Find the temperature of a blackbody if its spectrum has a peak at (a) λmax = 700 nm (visible), (b) λmax = 3 cm (microwave region) and (c) λmax = 3 m (FM radio waves) (Take Wien's constant b = 2.897 × 10-3 m K). (3 marks)
(a) λmax = 700 nm = 700×10-9 m, (b) λmax = 3 cm = 3×10-2 m, (c) λmax = 3 m b = 2.897 × 10-3 m K (a) T= b/λmax = (2.897 × 10-3 )/ (700×10-9) = 4138 K is the required temperature (b) T= b/λmax = (2.897 × 10-3 )/ (3×10-2) = 9.66×10-2 K is the required temperature (c) T= b/λmax = (2.897 × 10-3 )/ (3) = 9.66×10-4 K is the required temperature