Notes-Class 9-Science-Chapter-2-Work and Energy-Maharashtra Board

Topics to be learn : Work Positive, negative and zero work Energy Kinetic energy Potential energy Different forms of energy Law of conservation of energy Free fall Power

Introduction :

In everyday life, the word work is used to represent a physical or mental activity involving some effort.

Examples:

• A person climbing a staircase with a bag in his hand.
• A student reading a book.

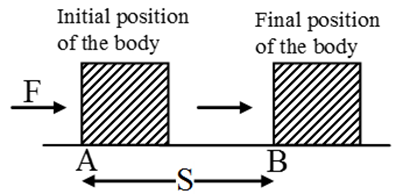
In scientific terms the word work is used under specific conditions. Work is said to be done by a force on a body when the body is displaced along the line of action of the force acting on the body.

Work :

Work : Work done by a force acting on a body is the product of the magnitude of the force and the displacement of the body in the direction of the force.

When the force (F) acting on the body and the displacement (s) of the body have the same direction, the work done by the force is W = Fs.

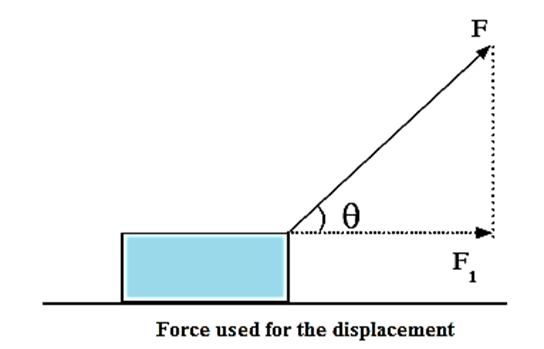
If q is the angle between the force F and displacement S, the work done by the force is W = Fs cos q

• If θ = 0°, cos θ = 1          ∴ W = Fs
• If θ = 90°, cos θ = 0      ∴ W = 0
• If θ = 180°, cos θ = −1  ∴ W = −Fs

• Work has magnitude, but not direction. Thus, it is a scalar quantity.
• The SI unit of work is the joule (J) and CGS unit is the erg.

The joule (SI unit of work) : The amount of work done when a force of one newton acting on an object displaces it through a distance of one metre along its own direction is called one joule.

The erg (CGS unit of work) : The amount of work done when a force of one dyne acting on an object displaces it through a distance of one centimetre along its own direction is called one erg.

1 joule = 1 newton x 1 metre

1J = 1 N-m

1 erg = 1 dyne x 1 centimetre = 1 dyne-centimetre

1J = 10⁷ ergs

Positive, negative and zero work

Positive work : When the force acting on the body and the displacement of the body have the same direction the work done by the force is positive.

• Example : When a worker climbs a staircase with some load on his head, the work done on the load by the force applied by the worker is positive.

Negative work : When the force and displacement have opposite directions. The work done is negative.

• Example : When a cyclist applies brakes to his bicycle and stops it or slows it down, the work done by the applied force is negative.

Zero work : If the displacement of the body is zero or if the displacement of the body is perpendicular to the force, or if there is no net force acting on the body, the work done is zero.

• Example : If a force applied on a big stone lying on the ground does not displace the stone, the work done by the force is zero.
• As in uniform circular motion where the force is always towards the centre of the circle and the displacement is always tangential therefore work done is zero in uniform circular motion.

Example : Let F = constant force acting on a body, s= displacement of the body and θ = angle between F and s. (Fig.)

Now, cos θ = OR/OQ

OR = OQ cos θ = F cos θ

This is the component of the force in the directionof the displacement.

\ Work done by the force, W = (F cos θ)s = Fs cos θ

θ	cos θ	W = F s cos θ	Conclusion
0°	1	W = F s	Work done is positive.
90°	0	0	Work done is zero.
180°	-1	W=-F s	Work done is negative.

• θ = 0° : In this case, the work done by the force is positive and maximum because the force and the displacement have the same direction.
• θ = 90° : In this case, the work done is zero because the displacement is perpendicular to the force.
• θ = 180° : In this case, the work done is negative and minimum as the displacement is in the direction opposite to that of the force.

Energy :

Energy :The capacity of a body to perform work is called its energy. It is a scalar quantity.

• Its units are the joule (SI unit) and the erg (CGS unit), same as work.

Two forms of mechanical energy : The two forms of mechanical energy are kinetic energy and potential energy.

Kinetic energy : The energy which an object has because of its motion is called its kinetic energy.

Example :

• A body falling under gravity has kinetic energy.
• A bullet fired from a gun has kinetic energy.

Kinetic energy cannot be negative. The mass (m) of a body cannot be negative. Also, the square of velocity (v²) cannot be negative. Hence, kinetic energy cannot be negative.

Correlation between work and energy :

• When man lifts a heavy bag, he has to do work against the earth’s gravitational force on the bag. In this process, the person loses a part of his energy and the bag gains an equal amount of energy.
• When one kicks a football, he performs some work on the ball. In this process, the person loses a part of his energy and the ball gains an equal amount of energy.

Thus, there is no fundamental difference between work and energy. Work is done due to transfer of energy.

Potential energy : The energy stored in an object because of its specific state or position is called its potential energy.

Example :

• Water stored in a dam possesses potential energy.
• A stretched spring possesses potential energy.

Gravitational potential energy of the body :

To lift the body from the ground level, work should be done against this force. This applied force should be numerically mg, but in the upward direction. The work to be done to take the body to a height h from the surface of the earth is

W = Fs = (mg)(h) = mgh.

The weight of a body of mass m is mg, where g is the gravitational acceleration of the body due to the earth. This force acts in the downward direction.

This work is stored in the body in the form of potential energy.

∴ Gravitational potential energy of the body = mgh.

∴ The gravitational potential energy of a body of mass m raised to a height ‘h’ above the ground level is mgh, where ‘g’ is the magnitude of the acceleration due to gravity at that position.

Transformation of energy :

Energy can be transformed from one type to another.

Different forms of energy : Mechanical energy (potential energy and kinetic energy), heat, light, sound, electrical energy, solar energy, chemical energy, nuclear energy, etc., are different forms of energy. Energy can be converted from one form to another.

• Chemical energy : The energy released from chemical reactions is called chemical energy.
• Nuclear energy : The energy released when heavy unstable atomic nuclei break up (fission) as well as the energy released when light elements combine to form a heavier element (fusion) is called nuclear energy. Nuclear energy can be converted into electrical energy.
• Solar energy is the energy radiated by the sun. It is in the form of heat, light, radio waves and other radiations. Solar energy can be converted into electrical energy. Plants use solar energy for photosynthesis.
• Heat energy needed to cook food is obtained by burning wood or biogas or LPG or using electricity or solar energy.

Law of conservation of energy : Energy can neither be created nor destroyed. It can be converted from one form into another. Thus, the total amount of energy in the universe always remains constant.

Q. How various forms of energy are interchangeable?

Free fall:

Free fall: An object falling solely under the influence of the gravitational force acting on it due to the earth is said to be in free fall or to be falling freely. Here, the effects of air (buoyancy and friction) are ignored.

The total energy (potential energy + kinetic energy) of a freely falling body remains constant during its motion.

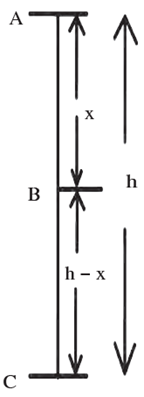
Conclusion : Every object has potential energy when it is at a height above the ground and it keeps getting converted to kinetic energy as the object falls towards the ground. On reaching the ground (point C), all the potential energy gets converted to kinetic energy. But at any point during the fall the total energy remains constant.

i.e., T.E. = P.E. + K.E.

T.E. at A = mgh + 0 = mgh

T.E. at B = mgx + mg (h - x) = mgh

T.E. at C = 0 + mgh = mgh

Power : Power is the time rate at which work is done.

• If W is the work done in time t, power (P) is given by P= W/t,
• It is a scalar quantity.
• The SI unit of power is the watt (W) and CGS unit is the erg per second.

If a device (or an appliance) does work at the rate of 1 joule per second, the power of the device is said to be 1 watt.

1 watt = 1 joule per second

          = 10⁷ ergs per second ………… (1 joule = 10⁷ ergs)

Power is also measured in unit horsepower (used in industry).

1 horsepower (hp) = 746 watts

The kilowatt-hour is a unit of energy used for commercial purpose.

1000 joule work performed in 1 second is 1 kilowatt power.

1 kW h = 1 kW x 1hr

           = 1000 W x 3600 s

            = 3600000 J

∴ 1 kilowatt-hour (KW.h) = 3.6 x 10⁶ J

The electrical energy used in house, industry, commercial establishment, etc., is expressed in kW.h.

Know This : Suppose an artificial satellite is moving around the earth in a circular orbit. As the gravitational force acting on the satellite (along the radius of the circle) and its displacement (along the tangent to the circle) are perpendicular to each other, the work done by the gravitational force is zero. Institutes at work: The National Physical Laboratory, New Delhi, was conceptualized in 1943. It functions under the Council of Scientific and Industrial Research. It conducts basic research in the various branches of physics and helps various industries and institutes engaged in developmental work. Its main objective is to establish national standards of various physical quantities.