Notes-Marathi Medium-Class 9-विज्ञान आणि तंत्रज्ञान-पाठ-1- गतीचे नियम-Maharashtra Board

अभ्यासघटक : वस्तूची गती विस्थापन आणि अंतर चाल व वेग एकरेषीय एकसमान ब नैकसमान गती त्वरण एकसमान गतीसाठी अंतर - काल आलेख नैकसमान गतीसाठी अंतर - काल आलेख एकसमान गतीसाठी वेग - काल आलेख एकसमान त्वरणित गतीसाठी वेग - काल आलेख आलेख पद्धतीने गतीविषयक समीकरणे एकसमान वर्तुळाकार गती न्यूटनचे गतीविषयक नियम संवेग अक्षय्यतेचा सिद्धांत.

वस्तूची गती (Motion of an Object) :

जर एखादी वस्तू सभोवतालच्या संदर्भात तिची जागा बदलत असेल, तर ती गतिमान आहे असे म्हणतात. वस्तू सभोवतालच्या संदर्भात तिची जागा बदलत नसेल, तर ती वस्तू स्थिर आहे असे म्हणतात.

• उदाहरण : पक्ष्याचे उडणे व हवेतून उडणारा पालापाचोळा यामध्ये गतीची जाणीव होते.
• वाहणारा वारा यात गती असते पण आपण प्रत्यक्ष पाहू शकत नाही.

विस्थापन आणि अंतर (Displacement and Distance) :

अंतर : अंतर म्हणजे दोन बिंदूंच्यादरम्यान गतिमान असताना वस्तूने प्रत्यक्ष केलेले मार्गक्रमण; म्हणजेच प्रत्यक्ष आक्रमिलेल्या मार्गाची लांबी होय. या राशीला परिमाण असते, पण दिशा नसते.

• एकक : अंतराचे SI एकक मीटर (मी, m) आहे व CGS एकक सेंटिमीटर (सेमी, cm) आहे.
• अंतर हि अदिश राशी आहे.

विस्थापन : विस्थापन म्हणजे गतिमानतेच्या आरंभ बिंदूपासून अंतिम बिंदूपर्यंतचे सर्वांत कमी अंतर होय. या राशीला परिमाण असते व दिशाही असते.

• एकक : विस्थापनाचे SI एकक मीटर (मी, m) आहे व CGS एकक सेंटिमीटर (सेमी, cm) आहे.
• विस्थापन हि सदिश राशी आहे

चाल व वेग (Speed and Velocity) :

चाल : एखाद्या वस्तूने एकक कालावधीत कापलेल्या अंतरास चाल म्हणतात.

• या राशीला परिमाण असते, पण दिशा नसते.
• या राशीचे SI एकक मीटर / सेकंद (मी / से, m/s) आहे आणि CGS एकक सेंटिमीटर/सेकंद (सेमी/से, cm/s) आहे.
• चालीचे मापन अंतर/काल याप्रमाणे सर्वप्रथम गॅलिलिओने केले होते. हवेतील ध्वनीची चाल 343.2 m/s तसेच प्रकाशाची चाल 3 ×10⁸ m/s इतकी आहे. पृथ्वीची सूर्याभोवती भ्रमण करण्याची चाल 29770 m/s आहे.

वेग : वेळेच्या संदर्भात होणाऱ्या विस्थापनातील दरास वेग म्हणतात.

• या राशीला परिमाण असते व दिशाही असते.
• वेगाचे SI एकक मीटर/सेकंद आहे व CGS एकक सेंटिमीटर/सेकंद आहे.

सरासरी चाल : एखाद्या वस्तूने एकूण कापलेले अंतर व ते अंतर कापण्यास लागलेला वेळ या गुणोत्तरास सरासरी चाल म्हणतात.

एखाद्या वस्तूने t₁, कालावधीत s₁, अंतर कापल्यास व नंतर t₂ कालावधीत s₂ अंतर कापल्यास, त्या वस्तूची (t₁ + t₂) या कालावधीतील सरासरी चाल = \(\frac{s_1+s_2}{t_1+t_2}\)

एकसमान गती : ज्या गतीमध्ये वस्तू खूप लहान व समान कालावधीत समान अंतर कापते, तिला एकसमान गती म्हणतात.

• उदा.: चाल कायम (स्थिर) असताना पंख्याच्या पात्यांची परिवलन गती.

नैकसमान गती : ज्या गतीमध्ये वस्तू समान कालावधीत असमान अंतर कापते, तिला नैकसमान गती म्हणतात.

• उदा. : पृथ्वीच्या गुरुत्वाकर्षणामुळे खाली पडणाऱ्या वस्तूची गती.

त्वरण :

त्वरण : वेगबदलातील दराला त्वरण म्हणतात.

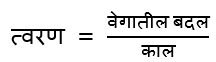
जर u हा सुरुवातीचा वेग, t या कालावधीनंतर बदलून अंतिम वेग v होत असेल तर ...

त्वरण = a = \(\frac{v-u}{t}\)

• या राशीला परिमाण असते व दिशाही असते.
• त्वरणाचे SI एकक मीटर/सेकंद² (मी/से², m/s²) आहे व CGS एकक सेंटिमीटर/सेकंद² (सेमी/से², cm/s²) आहे.

एकसमान त्वरण : जर खूप लहान व समान कालावधीत वस्तूच्या वेगामध्ये समान बदल होत असेल, तर वस्तूच्या त्वरणास एकसमान त्वरण म्हणतात

नैकसमान त्वरण : जर समान कालावधीत वस्तूच्या वेगामध्ये असमान बदल होत असेल, तर वस्तूच्या त्वरणास नैकसमान त्वरण म्हणतात.

धन , ऋण व शून्य त्वरण :

धन त्वरण : जेव्हा एखाद्या वस्तूचा वेग वाढत असतो, तेव्हा त्या वस्तूचे त्वरण धन असते.

a = \(\frac{v-u}{t}\), v > u असल्यास a धन असते.

• उदा., पृथ्वीच्या गुरुत्वाकर्षणामुळे खाली पडणाऱ्या वस्तूचे त्वरण धन असते.

ऋण त्वरण : जेव्हा एखाद्या वस्तूचा वेग कमी होत असतो, तेव्हा त्या वस्तूचे त्वरण ऋण असते. v < u असल्यास a ऋण असते.

• उदा., एखादी वस्तू वर फेकली असता, वर जात असताना त्या वस्तूचे त्वरण क्रण असते.
• वेग वाढत असताना त्वरण धन असते, तर वेग कमी होत असताना त्वरण ऋण असते. ऋण त्वरणाला अवत्वरण किंवा मंदन म्हणतात.

शून्य त्वरण : वेग एकसमान असल्यास त्वरण शून्य असते.

अंतर - काल आलेख :

अंतर - काल  आलेखाचे उपयोग : (i) ठरावीक वेळेस वस्तूचे स्थान काढण्यासाठी. (ii) ठरावीक वेळेस वस्तूची चाल काढण्यासाठी. (iii) वस्तूचे सरासरी त्वरण काढण्यासाठी.

 एकसमान गतीसाठी अंतर - काल आलेख :

खालील सारणीत एका गाडीने ठरावीक वेळेमध्ये कापलेली अंतरे दिलेली आहेत. त्यानुसार काल X अक्षावर व अंतर Y अक्षावर घेऊन काढलेला आलेख (आकृती).

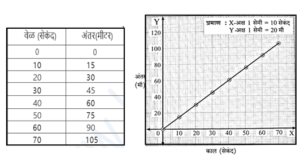
• या आलेखाच्या साहाय्याने अंतर व काल यांमधील समानुपाती संबंध स्पष्ट होतो. येथे वस्तूची गती एकसमान आहे हे स्पष्ट होते.
• एकसमान गतीमध्ये वस्तू समान कालावधीत समान अंतर कापते. हे अंतर – काल आलेखामधील सरळ रेषा दर्शवते.
• या आलेखावरील सरळ रेषेचा चढ म्हणजे गाडीची चाल होय.

चाल = \(\frac{s_2-s_1}{t_2-t_1}=\frac{90-15}{60-10}=\frac{75m}{50s}\)= 1.5 m/s

नैकसमान गतीसाठी अंतर - काल आलेख :

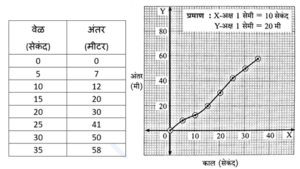
एकसमान गतीकरिता वेग – काल आलेख :

एक रेल्वे गाडी एकसमान वेगाने प्रती तास 60 कि मी या प्रमाणे 5 तास सातत्याने गतिमान आहे. या एकसमान गतीकरिता वेग आणि काल यांच्यातील बदल वेग – काल आलेखाने खालील आकृती मध्ये दर्शवला आहे.

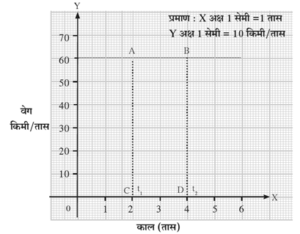
एकसमान त्वरणीत गतीकरिता वेग – काल आलेख

ठरावीक कालावधीनुसार एका कारच्या वेगात होणारे बदल सारणीत दिले आहेत.

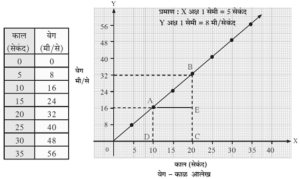
वरील आलेख दर्शवतो की,

• ठरावीक कालावधीत वेगामध्ये समान बदल होतो. हा वेग त्वरणीत असून त्वरण एकसमान आहे
• सर्व एकसमान त्वरणित गतीसाठी वेग - काल आलेख हा सरळ रेषा असतो.
• नैकसमान त्वरणित गतीसाठी वेग - काल आलेख वेळेनुसार वेगात होणाऱ्या बदलानुसार कोणत्याही आकाराचा असू शकतो.

गतीविषयक समीकरणे : वस्तूची गती एकरेषीय व त्वरण (a) एकसमान असताना,

• v =u + at ,.. (वेग - काल संबंध)
• s = ut + \(\frac{1}{2}\)at² .. (विस्थापन - काल संबंध)
• v² = u² + 2as (... (विस्थापन -- वेग संबंध)

येथे u = वस्तूचा सुरुवातीचा वेग, v = वस्तूचा t वेळानंतरचा वेग (अंतिम वेग), s = वस्तूचे t वेळातील विस्थापन होय.

एकसमान वर्तुळाकार गती (Uniform Circular Motion) :

एकसमान वर्तुळाकार गती : जेव्हा एखादी वस्तू एकसमान चालीसह वर्तुळाकार मार्गाने जाते, तेव्हा त्या गतीला एकसमान वर्तुळाकार गती म्हणतात. ही त्वरणित गती होय.

एकसमान वर्तुळाकार गती असणाऱ्या कणाच्या वेगाचे परिमाण (चाल)

येथे वस्तूची चाल, v = \(\frac{2πr}{t}\)    ...( r = वर्तुळाची त्रिज्या, t = वस्तूला एक फेरी पूर्ण करण्यासाठी लागणारा काल)

• एकसमान वर्तुळाकार गती असणाऱ्या कणाच्या वेगाची दिशा कणाच्या स्थानी वर्तुळाला कणाच्या गतीच्या दिशेने काढलेल्या स्पर्शिकेच्या दिशेने असते.
• उदाहरण : एकसमान चालीने फिरणाऱ्या गोफणीतील दगडाची गती, सायकलच्या चाकावरील कुठल्या ही बिंदूची गती.

न्यूटनचे गतीविषयक नियम (Newton’s Laws of Motion) :

न्यूटनचा गतीविषयक पहिला नियम : जर एखाद्या वस्तूवर कोणतेही बाह्य असंतुलित बल कार्यरत नसेल तर तिच्या विराम अवस्थेत किंवा सरळ रेषेतील एकसमान गतीमध्ये सातत्य राहते.

• न्यूटनचा हा नियम वस्तूच्या जडत्वाचे स्पष्टीकरण देतो. जडत्वाची सर्व उदाहरणे न्यूटनच्या या नियमाची उदाहरणे आहेत. म्हणून त्याला जडत्वाचा नियम म्हणतात.

संतुलित बल व असंतुलित बल (Balanced and Unbalanced Force) :

• एखादी वस्तू विराम अवस्थेत किंवा सरळ रेषेतील एकसमान गतीमध्ये असते तेव्हा तिच्या वर कोणतेही बल कार्य करत नसते असे नाही. प्रत्यक्षात त्या वस्तूवर विविध बाह्य बले कार्य करतात; परंतु ती परस्परांना निष्प्रभ करीत असल्याने एकंदर परिणामी बल शून्य होते.

संतुलित बल : ज्या वस्तूच्या आकारात व आकारमानात प्रयुक्त बलामुळे (फारसा) फरक पडत नाही, अशा वस्तूवर एकाच सरळ रेषेत समान परिमाणांची पण परस्परविरुद्ध दिशा असलेली दोन बले प्रयुक्त केली. या बलांना संतुलित बले म्हणतात; कारण या बलांचा वस्तूवरील एकत्रित परिणाम शून्य असतो.

• उदाहरण : टेबलावर ठेवलेल्या काचेच्या चिपेवर दोन संतुलित बले क्रिया करतात: (i) काचेच्या चिपेवर अधोगामी दिशेने क्रिया करणारे पृथ्वीचे गुरुत्वीय बल म्हणजेच वस्तूचे वजन व (ii) टेबलाच्या पृष्ठभागाने वस्तूवर ऊर्ध्वगामी दिशेने प्रयुक्त केलेले बल. या बलांचा वस्तूवरील एकत्रित परिणाम शून्य असल्याने ती वस्तू विराम अवस्थेतच राहते.

असंतुलित बल : जेव्हा वस्तूवर एकच बल क्रिया करते, तेव्हा ते असंतुलित बल असते. या बलामुळे वस्तूत त्वरण निर्माण होते. समजा, वस्तूवर दोन किंबा अधिक बले क्रिया करीत आहेत व परिणामी बल शून्य नाही. अशा वेळी परिणामी बल हे असंतुलित बल होय व

त्यामुळे वस्तूत त्वरण निर्माण होते.

• उदाहरण : जमिनीवर विराम अवस्थेत असलेल्या चेंडूला फटका मारल्यास तो प्रयुक्त बलामुळे गतिमान होतो.

बल : एखाद्या वस्तूच्या विराम अवस्थेत किंवा सरळ रेषेतील एकसमान गतिमान अवस्थेत बदल घडवून आणणारी भौतिक राशी म्हणजे बल होय.

• बल या राशीला परिमाण व दिशा दोन्ही असतात; म्हणजेच बल ही सदिश राशी आहे.
• वस्तूवर बल लावले असता, त्याचा वस्तूच्या गतीवर होणारा परिणाम किती बल लावले, म्हणजेच बलाचे परिमाण व ते बल कोणत्या दिशेने लावले यांवर अवलंबून असतो.

उदाहरण :

• एक चेंडू जमिनीवर विराम अवस्थेत आहे. त्या चेंडूला धक्का दिल्यास किंवा लाथ मारल्यास तो घरंगळत जातो. बल जेवढे जास्त लावावे तेवढी जास्त चाल चेंडूला प्राप्त होते.
• एखादी वस्तू सरळ रेषेत गतिमान आहे. तिच्यावर गतीच्या दिशेने बल लावल्यास वस्तूची चाल वाढते. परंतु गतीच्या विरुद्ध दिशेने बल लावल्यास वस्तूची चाल कमी होते.

वस्तूवर बल लावले असता, त्याचे वस्तूवर होणारे परिणाम :

• स्थिर वस्तू गतिमान होऊ शकते. उदाहरण : जमिनीवर स्थिर असलेल्या चेंडूला लाथ मारल्यास तो गतिमान होतो.
• गतिमान वस्तू स्थिर होऊ शकते. उदाहरण : ब्रेक वापरून गतिमान सायकल थांबवता येते.
• वस्तूची चाल बदलू शकते. उदाहरण : गतिमान सायकलचे ब्रेक दाबले असता, सायकलची चाल कमी होते.
• वस्तूच्या गतीची दिशा बदलू शकते. उदाहरण : एकसमान चालीने वर्तुळाकार फिरणाऱ्या वस्तूच्या गतीची दिशा प्रयुक्त बलामुळे सतत बदलत असते.
• वस्तूची चाल व वस्तूच्या गतीची दिशा, दोन्ही बदलू शकतात. उदाहरण : गोलंदाजाने टाकलेला चेंडू फलंदाजाने मारला असता, चेंडूची चाल व चेंडूच्या गतीची दिशा दोन्ही बदलतात.
• वस्तूचा आकार तसेच वस्तूचे आकारमान यांत बदल होऊ शकतो. उदाहरण : रबरी चेंडू दाबला असता, तो गोलाकार न राहता त्याचा आकार बदलतो. तसेच त्याचे आकारमानही कमी होऊ शकते.

जडत्व : वस्तूची स्थिर अथवा गतिमान अवस्थेतील बदलाला विरोध करण्याची प्रवृत्ती म्हणजेच जडत्व होय.

• विराम अवस्थेचे जडत्व, गतीचे जडत्व, दिशेचे जडत्व हे जडत्वाचे तीन प्रकार होत.

न्यूटनचा गतीविषयक दुसरा नियम (Newton’s second Law of Motion) : संवेग परिवर्तनाचा दर प्रयुक्त बलाशी समानुपाती असतो आणि संवेगाचे परिवर्तन बलाच्या दिशेने होते.

संवेग (Momentum) (P) : संवेग = वस्तूचे वस्तुमान × वस्तूचा वेग

P = mv.

• या राशीला परिमाण असते व दिशाही असते.
• संवेगाचे SI एकक किलोग्रॅम.मीटर/सेकंद (m/s) आहे व CGS एकक ग्रॅम.सेंटिमीटर/सेकंद (g.m/s) आहे.

न्यूटनचा गतीविषयक तिसरा नियम (Newton’s third Law of Motion) : प्रत्येक क्रिया बलास समान परिमाणाचे त्याच वेळी प्रयुक्त होणारे प्रतिक्रिया बल अस्तित्वात असते व त्यांच्या दिशा परस्परविरुद्ध असतात.

• बलाचे SI एकक न्यूटन (N) आहे व CGS एकक डाइन आहे.
• बल या राशीला परिमाण असते व दिशाही असते.

बल = वस्तुमान × त्वरण.

1 N = 1 kg-m/s², 1 dyne = 1 g.cm/s²

• निसर्गात बल एकांगी असू शकत नाही’. बल ही दोन वस्तूंमधील अन्योन्य क्रिया आहे. बले नेहमी जोडीनेच प्रयुक्त होत असतात. ज्या वेळी एक वस्तू दुसऱ्या वस्तूवर बल प्रयुक्त करते त्याच वेळी दुसरी वस्तू ही पहिल्या वस्तूवर बल प्रयुक्त करते. दोन वस्तू मधील बले नेहमी समान व विरुद्ध असतात.
• पहिल्या वस्तूने दुसऱ्या वस्तूवर प्रयुक्त केलेल्या बलास क्रिया बल तर दुसऱ्या वस्तूने पहिल्या वस्तूवर प्रयुक्त केलेल्या बलास प्रतिक्रिया बल म्हणतात.

संवेग अक्षय्यतेचा सिद्धांत (Law of Conservation of Momentum) :

संवेग अक्षय्यतेचा सिद्धांत : दोन वस्तूंची परस्पर क्रिया होत असताना, त्यांच्यावर जर काही बाह्य बल कार्यरत नसेल, तर त्यांचा एकूण संवेग स्थिर राहतो. तो बदलत नाही.

समजा, A या वस्तूचे वस्तु मान m₁ असून तिचा सुरुवातीचा वेग u₁आहे.

तसेच B या वस्तूचे वस्तु मान m₂ असून तिचा सुरुवातीचा वेग u₂ आहे.

संवेगाच्या सूत्रानुसार,

A वस्तूचा सुरुवातीचा संवेग = m₁u₁

B वस्तूचा सुरुवातीचा संवेग = m₂u₂

ज्या वेळी या दोन्ही वस्तू एकमेकांवरती आदळतील त्या वेळी A वस्तू वर B वस्तूमुळे F₁ बल प्रयुक्त होऊन A वस्तू त्वरणीत होते व तिचा वेग v₁ होतो.

∴ A वस्तूचा आघातानंतरचा संवेग = m₁v₁

न्यूटनच्या गतीविषयक तिसऱ्या नियमानुसार, A वस्तू देखील B वस्तूवर समान बल विरुद्ध दिशेने प्रयुक्त करते त्या वेळी तिच्या संवेगात बदल होतो.

समजा तिचा वेग v₂ झाल्यास

B वस्तूचा आघातानंतरचा संवेग = m₂v₂

जर B वस्तू वर F₂ बल प्रयुक्त होत असेल तर,

F₂ = — F₁

∴ m₂ a₂ = — m₁ a₁  …(‘.’ F= ma)

∴ \(m_2\frac{v_2-u_2}{t}=-m_1\frac{v_1-u_1}{t}\)

∴ m₂ (v₂ - u₂ ) = - m₁ (v₁-u₁)

∴ m₂ v₂ - m₂ u₂ = - m₁ v₁ + m₁ u₁

∴ (m₂ v₂ + m₁ v₁ ) = (m₁ u₁ + m₂ u₂)

एकूण अंतिम संवेगाचे परिमाण = एकूण सुरुवातीच्या संवेगाचे परिमाण

म्हणजेच, दोन्ही गोलांचा आघातानंतरचा एकूण संवेग हा त्यांच्या आघातापूर्वीच्या एकूण संवेगाइतका असतो.

यावरून असे दिसते की, बाह्य बलाची क्रिया होत नसताना जेव्हा दोन वस्तूंची टक्कर होते, तेव्हा त्या वस्तूंचा आघातापूर्वीचा एकूण संवेग हा त्यांच्या आघातानंतरच्या एकूण संवेगाइतका असतो ( संवेग अक्षय्यतेचा सिद्धांत ).

संवेग अक्षय्यतेचा सिद्धांत उदाहरण  : (बंदुकीतून मारलेल्या गोळीचे उदाहरण)

जेव्हा m₁ वस्तु मानाची गोळी m₂ वस्तु मानाच्या बंदुकीतून मारली जाते, तेव्हा वेगाने पुढे जाताना तिचा संवेग m₁v₁ होतो.

गोळी उडवण्या पूर्वी बंदूक आणि गोळी स्थिर असल्याने सुरुवातीचा संवेग शून्य असतो व एकूण संवेग शून्य असतो.

गोळी उडविल्या नंतरदेखील वरील नियमाप्रमाणे एकूण संवेग शून्य असतो.

गोळीच्या पुढे जाण्यामुळे बंदूक मागच्या दिशेने सरकते. या सरकण्याला ‘प्रतिक्षेप’ (Recoil) म्हणतात.

बंदूक प्रतिक्षेप वेगाने (v₂) अशा पद्धतीने सरकते, की

m₁ v₁ + m₂ v₂ = 0 किंवा v₂ = \(-\frac{m_1}{m_2}v_1\)

• बंदुकीचे वस्तुमान गोळीच्या वस्तु मानापेक्षा बरेच जास्त असल्याने बंदुकीचा वेग गोळीच्या वेगाच्या तुलनेने अगदी कमी असतो. बंदुकीचा संवेग व गोळीच्या संवेगाचे परिमाण सारखे व दिशा विरुद्ध असतात. त्यामुळे तेथे संवेग स्थिर असतो.
• अग्निबाण (रॉकेट ) प्रक्षेपणातही संवेग स्थिर असतो.